95%信頼区間の求め方や計算式とは？有意差やなぜ1.96なのかの意味と論文の書き方まで

• 95%信頼区間ってよく目にするけど、一言でいうと何・・・？
• 95%信頼区間はどうやって解釈すればいい・・・？
• 95%信頼区間はどんな時に活躍するの・・・？
• 95%信頼区間と有意差の関係は・・・？

　

統計を勉強すると必ず出てくる95%信頼区間。

でもいまいちその意味がわからない。。

95％信頼区間では1.96という数字もよく見るけど、なぜ1.96なのかがわからない。

そんな95％信頼区間について、計算式や1.96の意味、そして有意差との関係まで解説します！

　

95%信頼区間とは？平均値と標準偏差の重要性

　

連続量のデータを集計する時、あなたは何を要約統計量として計算しますか？

おそらく一番最初に頭に浮かぶのは「平均値」ですよね。

で、その次が「標準偏差（もしくは分散）」ではないでしょうか。

　

その思い浮かべ方、正解です！

私も真っ先に平均値と標準偏差を計算します。

この２つはそれほど重要な指標ってことです。

　

ですが、実は平均値と標準偏差を計算しただけではまだ不十分です。

なぜなら、平均値が「点」推定だからです。

　

・・・「点」推定である、ってどういうこと？

・・・「点」があるなら、違う推定もある？？

　

そう思いましたよね。

ということで、大学生の体重の例を使ってみましょう。

　

95%信頼区間の必要性を理解する：10人（母集団）のうちの5人（標本）の平均値は？

この表にある、10人のデータが母集団だとします。

大学生1	大学生2	大学生3	大学生4	大学生5	大学生6	大学生7	大学生8	大学生9	大学生10
50.4	54.6	55.2	58.4	64.3	65.5	69.1	71.4	74.5	88.3

　

その時の母集団の平均値（母平均）は65.17です。

では、この10人の母集団から、5人の標本の体重の平均値を出してみます。

　

　

あなたは、この結果から何を見出しますか？

見やすいように、母平均と、各標本の平均値を並べます。

母平均	標本１の平均	標本２の平均	標本３の平均
65.17	56.58	62.5	68.48

　

重要な事実があります。

それはこれ。

　

　

そうですよね。言われてみれば当たり前な気がします。

標本１も標本２も標本３も、その平均値は母平均とは違います。

つまり、あるデータの平均値（代表値）は、そのデータだからその平均値になっただけであって、必ずしも母集団の平均値とは一致しないということです。

この当たり前な事実がとても重要な事実なのです。

　

そして平均値は、数字が一つの「点」で示された要約統計量で母集団を推定しようとしています。

そのため、「点」推定と呼ばれているのです。

　

95%信頼区間を理解するには”区間推定”を理解する

　

上記の例で、各標本の平均値は母集団の平均値とは違うという事実を知りました。

つまり、点推定（平均値）だけでは母集団の平均値を示すのに、不十分であるということです。

　

では、どうすればよいか？

それは、線（区間）の推定を行えばよいということです。

推定とは、標本から母集団を特定する事。

そのため、母集団の平均値はこれだ！と、点で表すのではなく、母集団の平均値は、これぐらいの間にあるはず、というように区間で示す必要があるのです。

　

95%信頼区間とは一言でいうと何？

区間推定を表す指標の代表的なものが、95%信頼区間（95% Confidence Interval; 95%CI）です。

データを扱ったことのある方であれば、95%信頼区間という言葉は聞いたことがあると思います。

しかし、それが何を意味するか？まで知っている人は、少ないのではないでしょうか。

ここで整理しておきましょう。

95%信頼区間は、区間推定の代表的な指標です。

　

誤解を恐れずに95%信頼区間を一言で表してみます。

　

95%信頼区間を理解するために標準誤差を理解する

95%CIを理解するためには、標準誤差（Standard Error; SE）というものを理解する必要があります。

標準誤差は標準偏差と用語が似ています。

ですが、あなたはその違いを説明することが出来ますか？

　

今は説明できなくても大丈夫です。

それほど難しくはありません。

標準誤差は以下の数式で求めることが出来ます。

　

標準誤差（SE） = 標準偏差（SD）/sqrt(n)

　

ここでnというのは、データの数を表しています。

で、sqrt()というのは、（）内の数字の平方根（ルート）、という意味です。

つまり、nが大きい=データの数が大きいほど、SEは小さくなるという性質があります。

このnが大きい=データの数が大きいほど、SEは小さくなるという性質が、そのまま95%信頼区間にも当てはまります。

そのため、この性質は絶対に把握しておきましょう！

　

データの数が変わると標準偏差と標準誤差のどっちが変わる？

例えば、20歳の身長の平均値を知りたいとします。

その時に、ある研究チームは50例のデータが得られ、もう一方の研究チームは1000例のデータが得られたとします。

そして、これらの2つのチームデータは平均値165cm、標準偏差20という、全く同じ要約統計量が算出されました。

このとき、どちらのデータが信頼性が高いでしょうか？

直感的にも、1000例のデータの方が信頼性が高いと思いませんか？

　

この時の2つのデータの標準誤差を計算してみましょう。

前者のデータの標準誤差は、20/sqrt(50)=2.83です。

後者の標準誤差は、20/sqrt(1000)=0.63になります。

　

標準誤差は推定値（平均値など）の信頼性を表す。

上記の通り、全く同じデータのバラつきでも、データが多いか少ないかで、その要約統計量（平均値など）の情報の信頼性というのは異なります。

そして、データが多いほど標準誤差は小さくなります。

標準誤差の使い方は、平均値（標準誤差）という使い方が普通です。

つまり、標準誤差とは推定値（平均値など）の信頼性を表す指標です。

重要なのでもう一度書きます。

標準偏差はデータのバラつきの指標であるのに対し、標準誤差は推定値（平均値など）の信頼性を表す指標

　

ここで推定値（平均値など）と示したのは、標準誤差は平均値に限らない指標だからです。

この例では平均値で解説しましたが、平均値は推定値の中の一つですので、標準誤差は一般的に、推定値の信頼度合いを示す指標だと思っていただければと思います。

推定値には、リスク比だったりオッズ比だったりハザード比だったり最小二乗平均値だったり割合だったりが含まれています。

では95%信頼区間の求め方や計算式は？1.96の意味は？

標準誤差が理解できれば、95%CIを理解することは簡単です。

正規分布の場合の95%CIの計算式は、95%CI=1.96*SEで計算できます。

簡単ですね。

ここで、１つだけ注目したいところがあります。

それは1.96という数値です。

どこかでみたことのある数字だと思います。

　

正規分布の説明で“1.96SDの範囲の中に95%のデータが含まれる”という話をしました。

この1.96と、95%信頼区間の計算に登場する1.96は本質的に同じものです。

というのも、95%信頼区間の概念はこのようなものだからです。

　

　

　

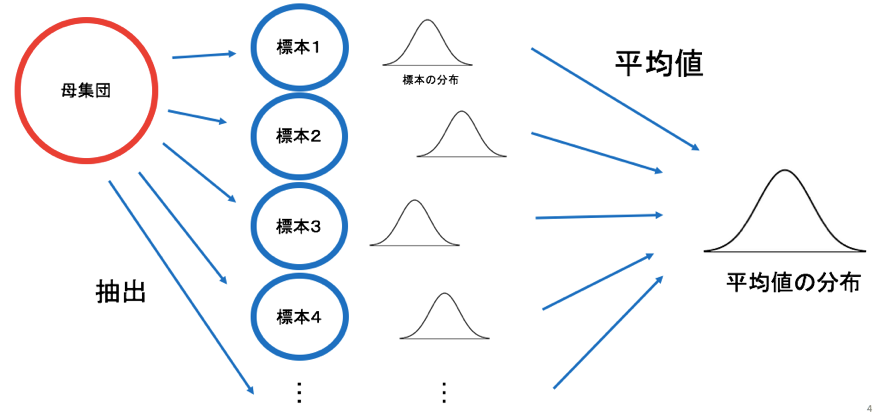
まず、母集団から抽出された標本データを、われわれは扱っています。

その標本から平均値が１つ算出できます。

そして、標本を複数集めると、複数の平均値が得られます。

ちょうど、先ほど計算した、男子大学生の身長に関しての5つの標本平均が得られた状況です。

すると、標本平均を集めると平均値の分布を書くことができますよね。

　

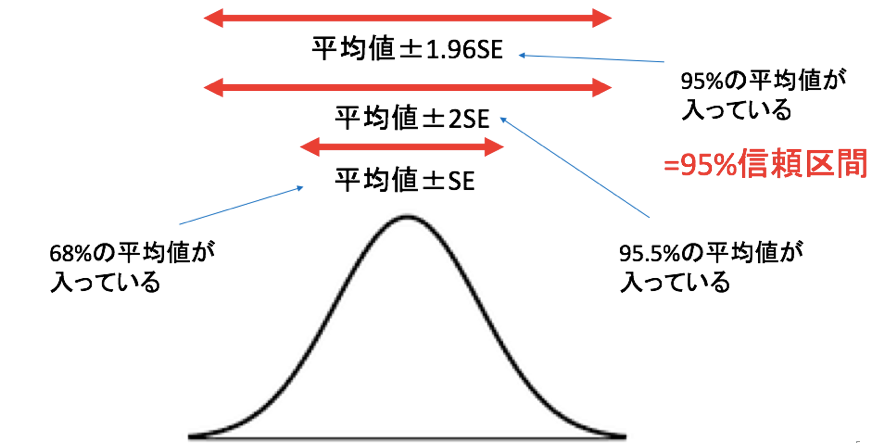
その平均値の分布が正規分布であると仮定できるとき、正規分布の性質は、平均値±SDの中に約68％のデータが含まれており、平均値±2SDの中に約95.5%のデータが含まれるということでした。

　

この性質が、今回の平均値の分布にも当てはめることができます。

つまり、平均値±SEの中に約68％の平均値が含まれており、平均値±2SEの中に約95.5%の平均値が含まれる、ということです。

そして95%ちょうどの平均値が含まれる範囲が、平均値±1.96SEということになります。

これが95%信頼区間のイメージです。

95%信頼区間の解釈について注意点

そして重要なことは、95%CIが何を表しているか、です。

突然ですが、95%信頼区間と聞いて、皆さんが想像するのは以下のうちどちらでしょうか？

　

正解は2です。

これは混同しやすいので注意が必要です。

真値は真の値ですから、必ず1つだけです。

1の場合ですと、95%信頼区間が固定されており、真値が動いているイメージです。

違います。

真値が固定されていて、95%信頼区間がデータによって変わりうるのです。

この概念は非常に重要ですので、しっかりと理解してください。

　

95%信頼区間と有意差の関係：0をまたぐ、1をまたぐことの意味

ここで、95%信頼区間と有意差の関係を理解しましょう。

まず結論から言うと、このような関係があります。

差の場合は0を跨いでいないかどうか

ここで、”帰無仮説で設定した数値”とありますが、例えば平均値の検定であるT検定。

帰無仮説は「A群の平均値＝B群の平均値」ですね。

つまりT検定での帰無仮説は、「A群の平均値ーB群の平均値＝０」となります。

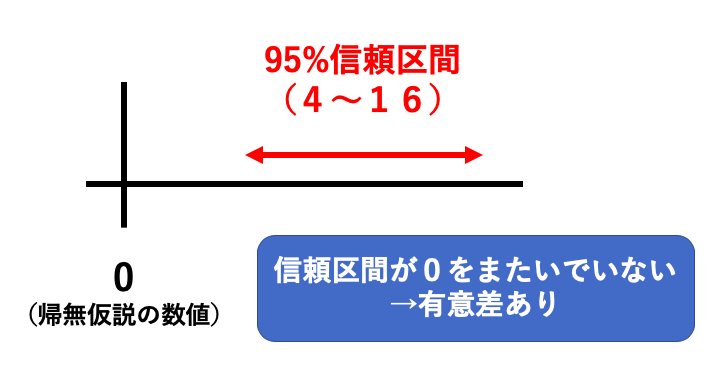
この時、「A群とB群の平均値の差が１０であり、その95%信頼区間が４〜１６だった」という場合。

この場合には、95%信頼区間が０（帰無仮説で設定した数値）をまたいでいないため、有意差あり、となります。

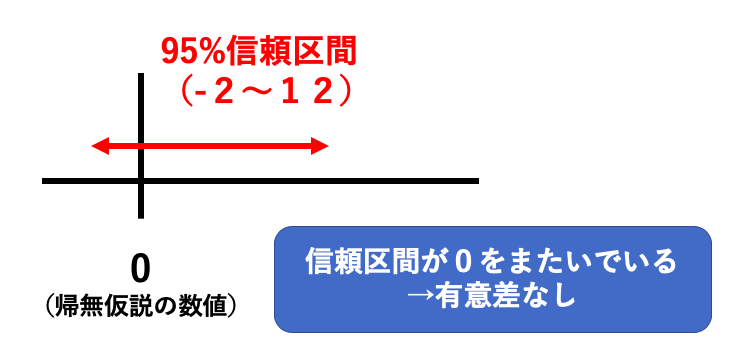
では次に「A群とB群の平均値の差が５であり、その95%信頼区間が−２〜１２だった」という場合。

この場合には、95%信頼区間が０（帰無仮説で設定した数値）をまたいでいるため、有意差なし、となります。

　

オッズ比やリスク比の場合は1をまたぐかどうか

95％信頼区間は”帰無仮説で設定した数値”を跨いでいなければ、有意だと見分けることができます。

上記の例ではt検定を例にしたので、差の95％信頼区間が0を跨いでいなければ有意差あり、となっていました。

では、オッズ比やリスク比だとどうなるでしょうか。

詳しい解説は省略しますが、”95%信頼区間が1を跨いでいなければ有意”と見なすことができますね。

ぜひこの見方は理解しておいてください。

　

95%信頼区間の論文での書き方例

95%信頼区間について理解していただいたところで、最後に論文での書き方をお伝えします。

例えばこちらの論文のように、点推定値（95%信頼区間）という形で記載されていることが多いため、そのように記載いただければ問題ありません。

 The percentage reductions were −43.7% (95% confidence interval [CI], −53.4 to −34.0) with 0.1 mg of nemolizumab per kilogram (P=0.002), −59.8% (95% CI, −69.4 to −50.3) with 0.5 mg per kilogram (P<0.001), and −63.1% (95% CI, −72.9 to −53.3) with 2.0 mg per kilogram (P<0.001), as compared with −20.9% (95% CI, −31.4 to −10.5) with placebo. (引用：N Engl J Med 2017;376:826-835)

95%信頼区間に関するまとめ

• 推定は、点推定だけでは不十分であり、区間推定を実施する必要がある。
• 95%信頼区間が区間推定の代表である。
• 95%信頼区間とは、仮に100回試験をした場合、100回中5回くらいは真値を含まないことがある、ということを意味する。