R で多重代入法を実行した後に Fine-Gray 回帰を行う方法

2023年2月21日2024年9月1日

多重代入法で欠測値を補完し、Fine-Gray 回帰を実施する方法

＞＞もう統計で悩むのは終わりにしませんか？

↑期間・数量限定で無料プレゼント中！

サンプルデータ

競合リスクを含むイベント変数、時間変数、着目したい変数、交絡因子を以下のとおりとする

競合リスクを含むイベント変数：CompRisk
時間変数：DaysFPS
着目したい変数：PS34
交絡因子：Age, CR12

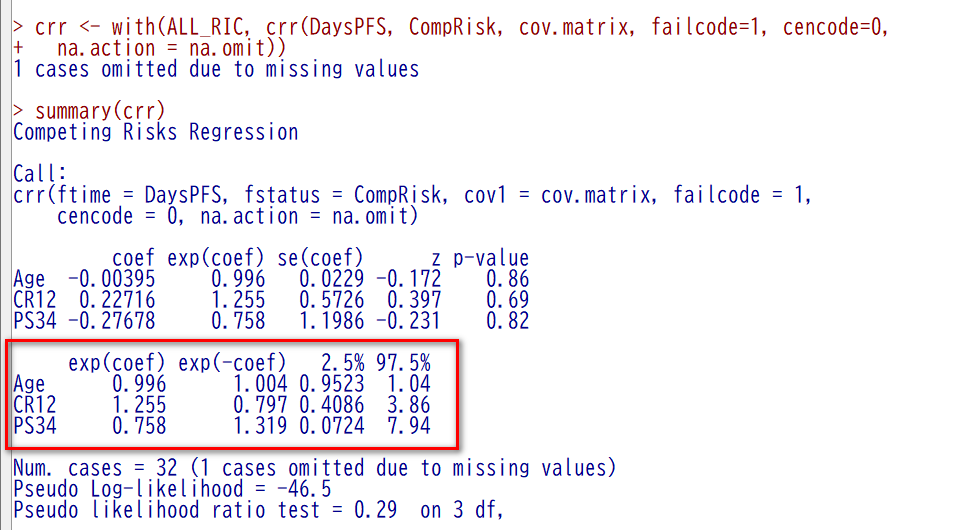
欠測値の数を確認すると、PS34 に 1 例だけ欠測値があることがわかる

Fine-Gray 回帰を実施した結果

EZR で、以下のように設定して、Fine-Gray 回帰を実行する

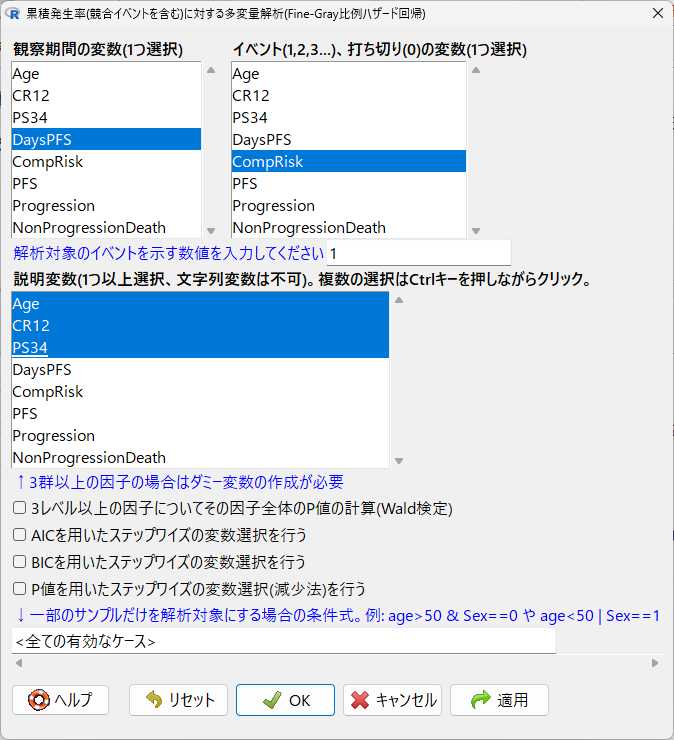
実行した結果はこちら

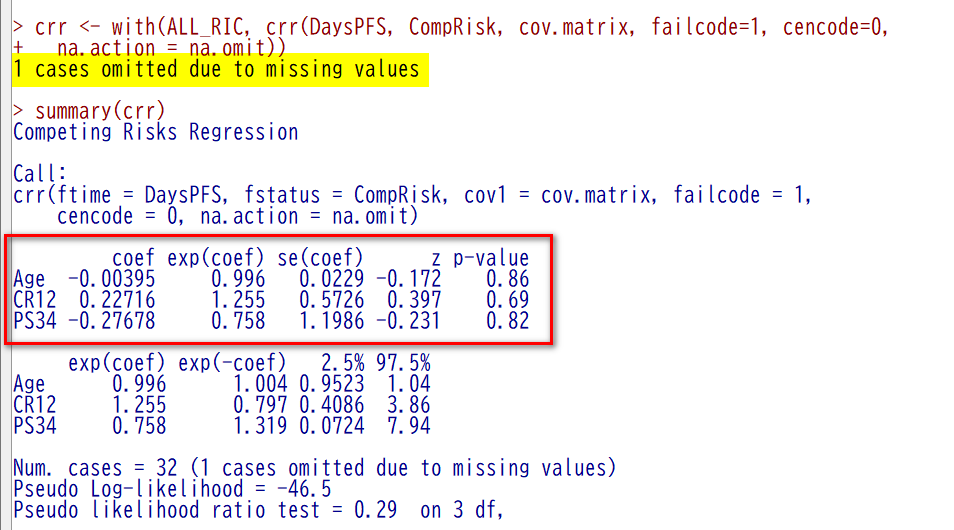
赤枠部分が、結果のメインである

黄色ハイライトのように、1 cases omitted due to missing values とあって、欠損値のために 1 例除外しているとある

＞＞もう統計で悩むのは終わりにしませんか？

↑1万人以上の医療従事者が購読中

欠測値を多重代入する方法

R の mice パッケージの mice() 関数を使って、欠測値を多重代入する

install.packages('mice') # まだインストールしていない場合
library(mice)

データセットの名前を dat とする

多重代入したデータセットの名前は imp とする

再現性を持たせるために、seed = 123 とセットする

dat <- ALL_RIC
imp <- mice(dat, seed=123)

imp の中は、5 の多重代入したデータセットになっている

pmm という方法で PS34 が多重代入されているのがわかる

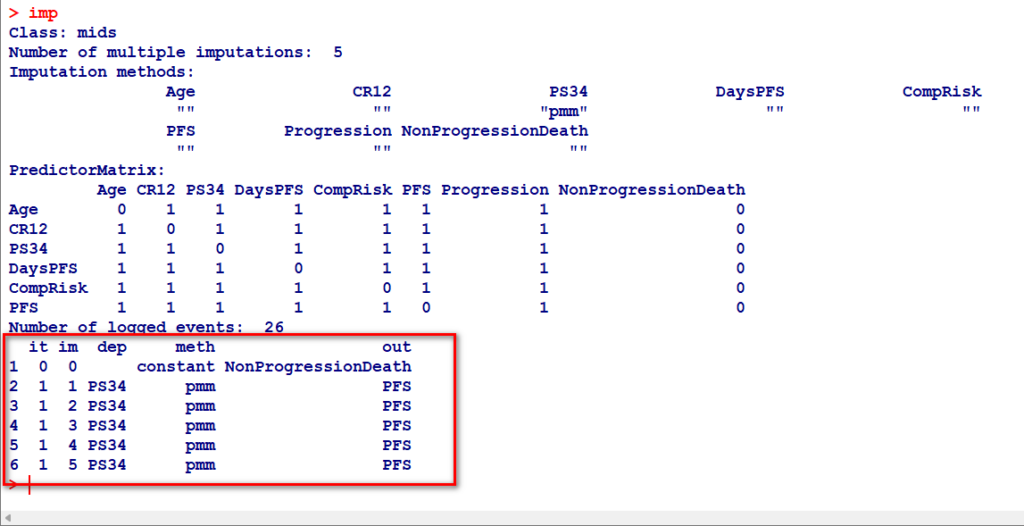
PS34 の欠測値の部分（症例番号 21 ）に代入された値は、4 つのデータセットは 0 で、1 つのデータセットだけ 1 であることがわかる

多重代入したデータで Fine-Gray 回帰を行う方法

多重代入したデータで Fine-Gray 回帰を行うために、adjustedCurves パッケージを使う

FGR_MI() 関数を使うために、prodlim パッケージの Hist() 関数も使えるようにする

install.packages( c('adjustedCurves', 'prodlim') ) # まだインストールしていない場合
library(adjustedCurves)
library(prodlim)

FGR_MI() 関数で解析する

イベント変数は、値が 0, 1, 2 となっていて、1 が解析したいイベント（ cause=1 ）である

model.fgr <- FGR_MI(mids=imp, formula=Hist(DaysPFS, CompRisk) ~ Age + CR12 + PS34, cause=1)
model.fgr

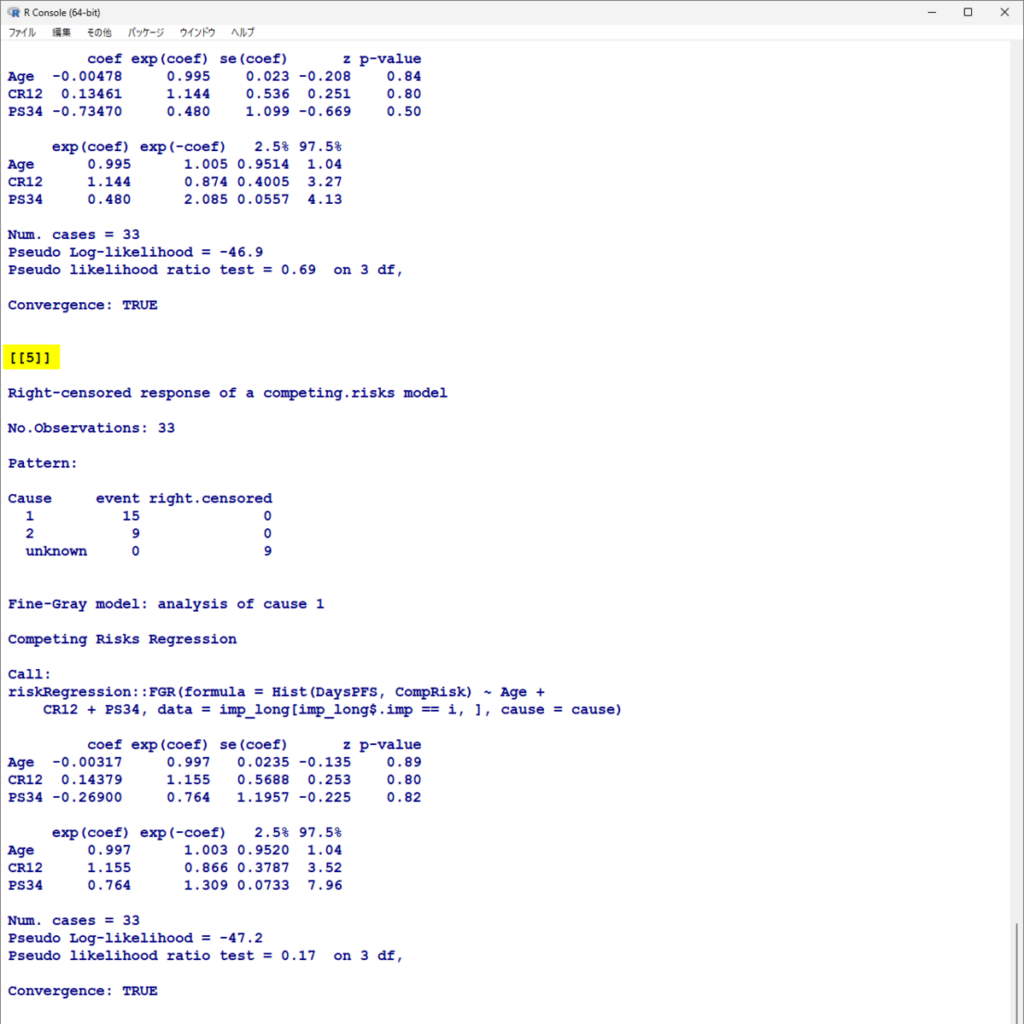
結果を表示すると 1 から 5 まで 5 つの解析結果が格納されているのがわかる

1 と 2 の先頭まで

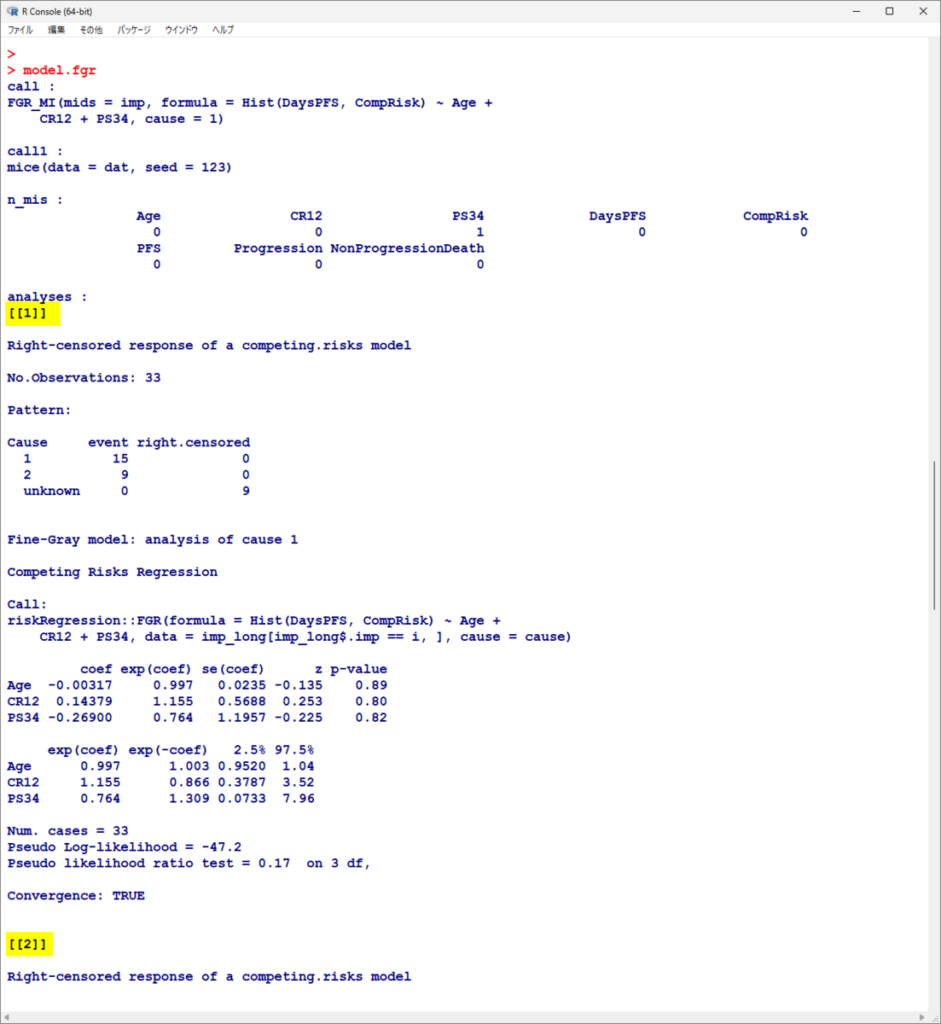
5 の結果

結果を統合する方法

結果を統合するために平均と分散を取り出す

ests に平均値、vars に分散を格納する

ests <- list()
vars <- list()
for (i in 1:5) {
ests[[i]] <- model.fgr$analyses[[i]]$crrFit$coef
vars[[i]] <- diag(model.fgr$analyses[[i]]$crrFit$var)
}
ests
vars

5 つの解析結果を並べてみると、4 つ目のデータセットだけ結果が異なることがわかる

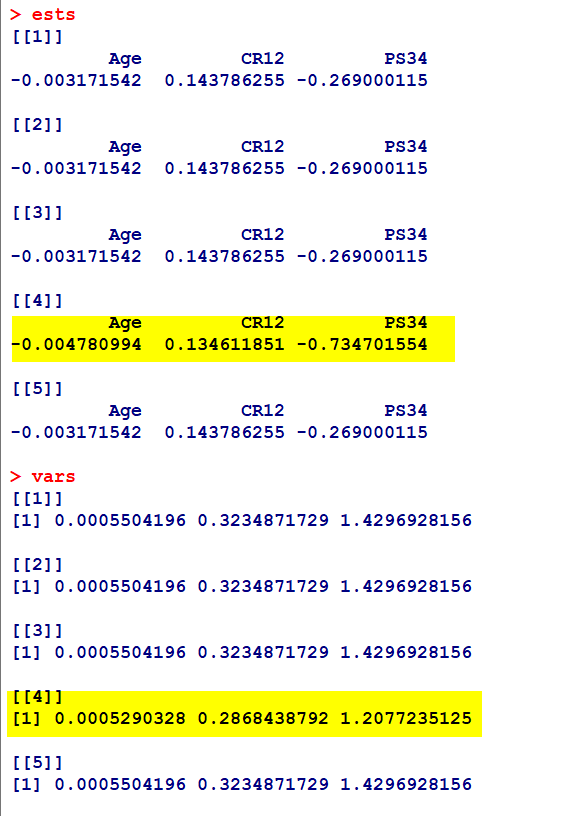
これは上記で、4 つ目のデータセットだけ PS34 に 1 が代入されていたことと連動している

次に、mitools パッケージの MIcombine() 関数で、結果を統合する

summary() できれいに出力し、exp() で対数から真数に変換している

MIcombine(ests, vars) # 結果の統合
summary(MIcombine(ests, vars)) # 統合した結果のきれいな出力
summarized <- summary(MIcombine(ests, vars)) # 出力をいったんオブジェクトに
summarized[c(1,3,4)] # 点推定値と信頼区間下限・上限のみ抜き出し
exp(summarized[c(1,3,4)]) # 点推定値と信頼区間の真数への変換