サンプルの連続データが正規分布していない場合に、平均値の 95 % 信頼区間を計算する方法
正規分布していない連続データが対数正規分布だった場合
正規分布していない連続データを対数変換すると正規分布に見える場合、その連続データは対数正規分布のデータと考えられる
例えば、このようなヒストグラムの場合は、正規分布していないと言える
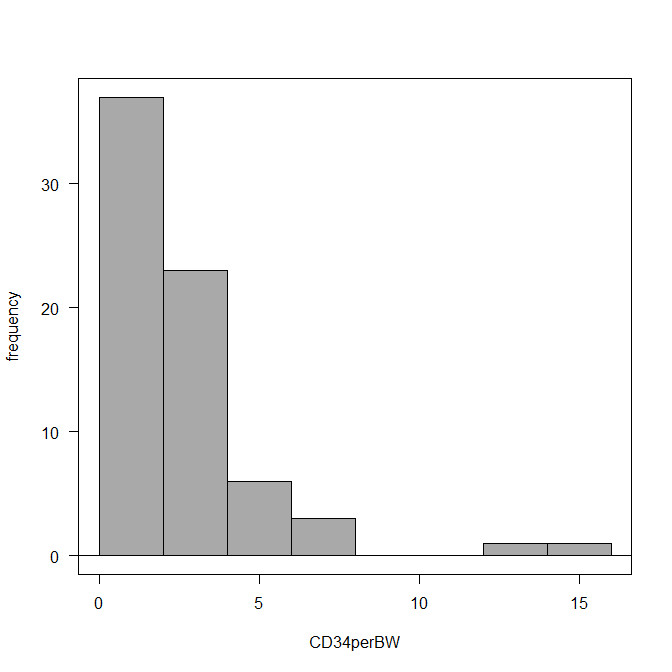
対数に変換したのちヒストグラムを書くとこのように正規分布のようになる場合、対数正規分布のデータと考えられる
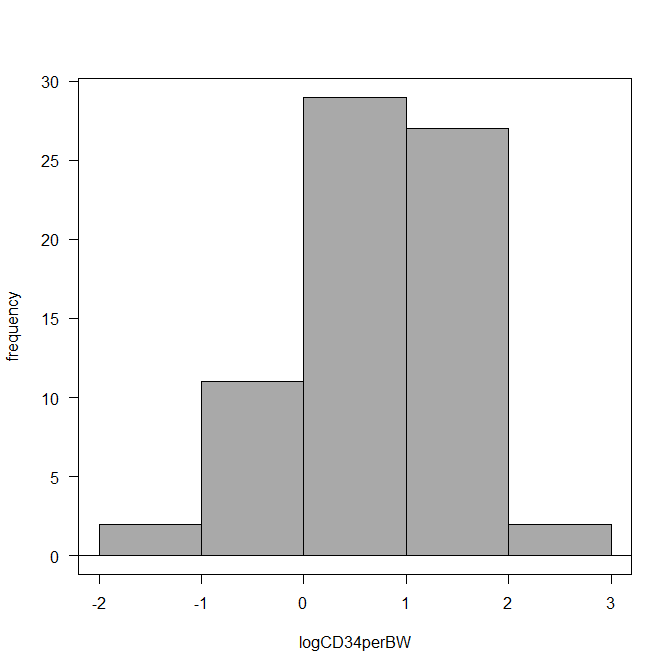
正規分布していない連続データから平均値の 95 % 信頼区間を計算する方法
対数正規分布の連続データの場合、95 % 信頼区間を対数で計算し、真数に戻す方法がとれる
そのままのデータで 95 % 信頼区間を計算した場合と比較してみる
まず、平均値と標準偏差を計算する

この平均値と標準偏差を使って 95 % 信頼区間を計算する
計算には、EZR の平均値の信頼区間の計算メニューを使う
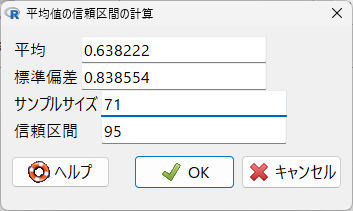
このように入力すると以下のように出力される

この中の、CIL、CIH、se の計算式を活用して以下のように計算してみる
それぞれ、平均値、95 % 信頼区間下限値、95 % 信頼区間上限値の順に並べて出力している
# 対数変換した値で計算した 95 % 信頼区間
> c(0.638222, 0.638222 - qt((100+95)/200, 71-1)*0.838554/ sqrt(71), 0.638222 + qt((100+95)/200, 71-1)*0.838554/ sqrt(71))
[1] 0.6382220 0.4397395 0.8367045
# 真数に戻した 95 % 信頼区間
> exp(c(0.638222, 0.638222 - qt((100+95)/200, 71-1)*0.838554/ sqrt(71), 0.638222 + qt((100+95)/200, 71-1)*0.838554/ sqrt(71)))
[1] 1.893112 1.552303 2.308746
# そのままの値で計算した 95 % 信頼区間
> c(2.632254, 2.632254 - qt((100+95)/200, 71-1)*2.4420455/ sqrt(71), 2.632254 + qt((100+95)/200, 71-1)*2.4420455/ sqrt(71))
[1] 2.632254 2.054231 3.210277
正規分布していない連続データから平均値の 95 % 信頼区間を計算してヒストグラムに重ねる
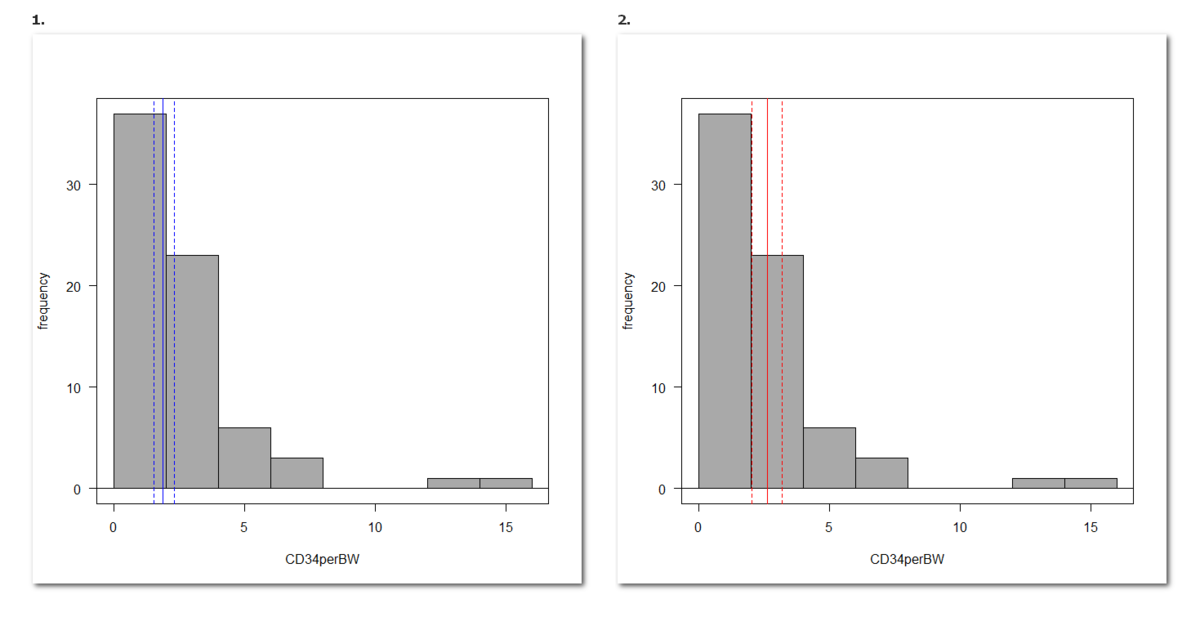
ヒストグラムに重ねてみると以下のようになる
のグラフの青点線の区間が、対数変換して真数に戻した 95 % 信頼区間である
のグラフの赤点線の区間が、そのままの値で計算した 95 % 信頼区間である
実線は、それぞれの方法で計算した平均値である
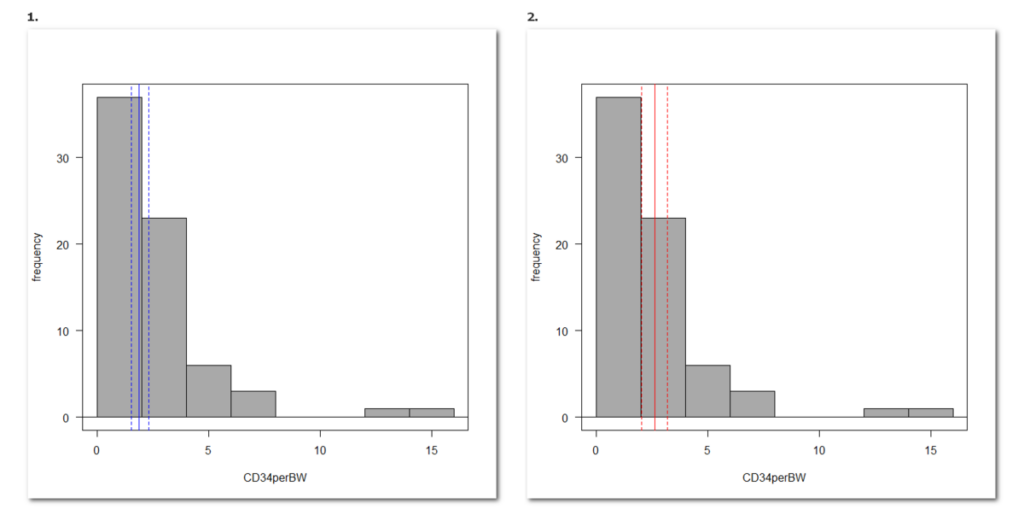
青に比べると、赤のほうが、平均が大きい値に引っ張られていて大きくなっており、ばらつきも大きい値に引っ張られ広めになっている
赤の点線は、実線からの距離が等距離だが、青の点線は、等距離ではない
これは、対数では等距離だが、真数にすると大きい値のほうがより大きくなるためである
まとめ
正規分布していない連続データで、対数正規分布している場合の平均値の 95 % 信頼区間の計算を解説した
対数に変換し、平均値と標準偏差を計算し、それらを使って 95 % 信頼区間を計算する
平均値と 95 % 信頼区間下限と上限の値を真数に戻す
このようにすれば、対数正規分布の連続データの平均値の 95 % 信頼区間が計算できる
関連記事

おすすめ書籍
EZR公式マニュアル






コメント