重回帰分析に交互作用を含んだ解析をSPSSで計算する方法。
SPSSの重回帰分析では、交互作用項を自動で作ってくれない。
どのように作って、どのように解析すればよいか？
SPSSで交互作用項の作り方
重回帰モデル内で交互作用の検討をするためには、交互作用項を投入する必要がある。
交互作用項とはどういうもので、どのように作るのか？
交互作用項は、性別などのカテゴリカルデータと、白血球数などの連続データの掛け算の項のことを言う。
カテゴリカルデータはダミー変数に変換する。
掛け算するとダミー変数で１としているカテゴリのみ数値が入った変数ができる。
これが交互作用項である。
SPSSではどのように作るのか？
SPSSで交互作用項を作るためにダミー変数を作成する
その１：ダミー変数の作成メニューを使う方法
「変換」→「ダミー変数を作成」を選択する。
例えば、性別 (gender) を赤枠のところに入れる。
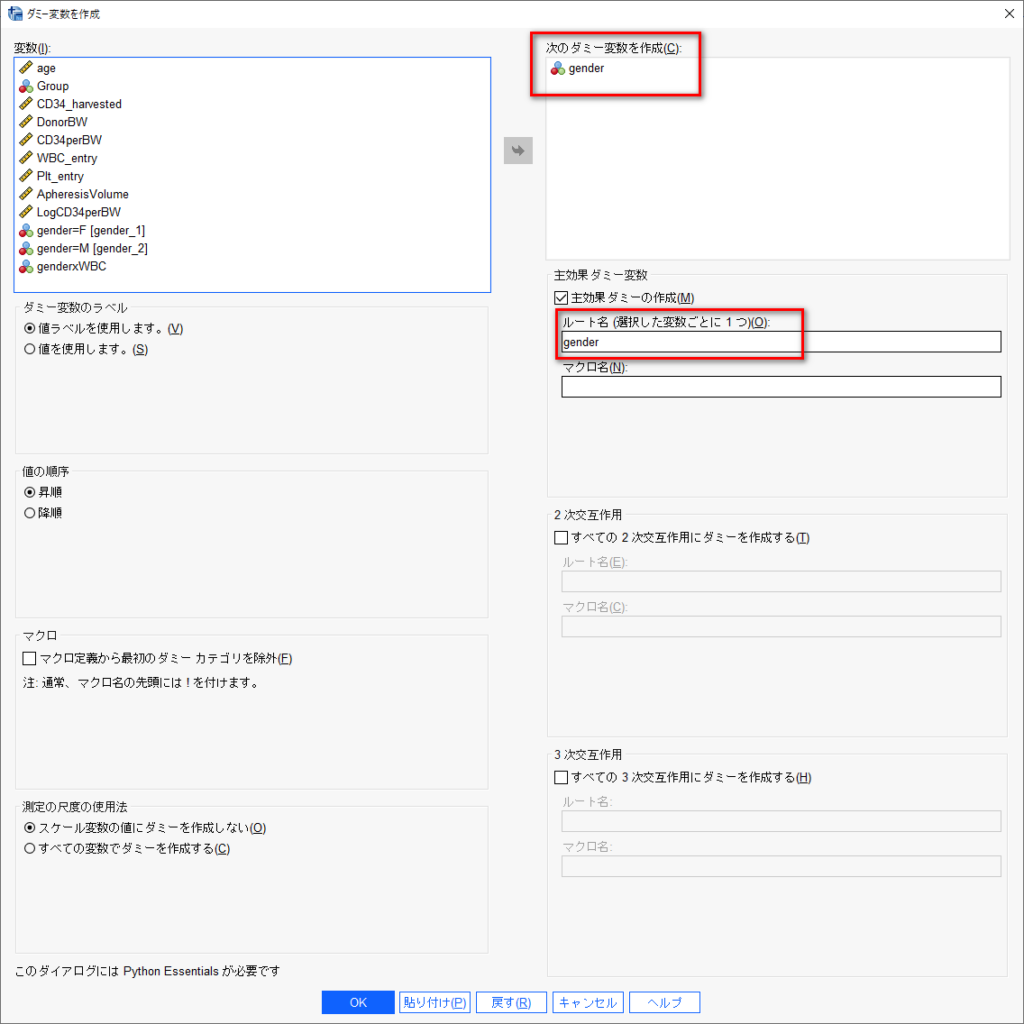
OKをクリックすると変数ができる。
右端の赤枠が出来上がりのダミー変数である。
左端の赤枠と照らし合わせてみると、どのように作成されているか規則がわかる。
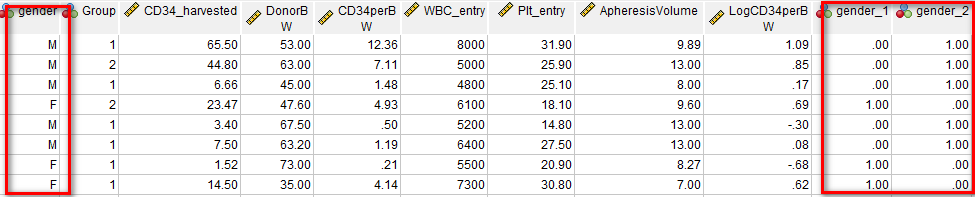
その２：他の変数への値の再割り当てを使う方法
上記の方法がうまくいかなければ、「変換」→「他の変数への値の再割り当て」を使って、例えば今回の場合、性別Fを１、Mを0とする変数を作成する。
SPSSで交互作用項を計算によって作成する
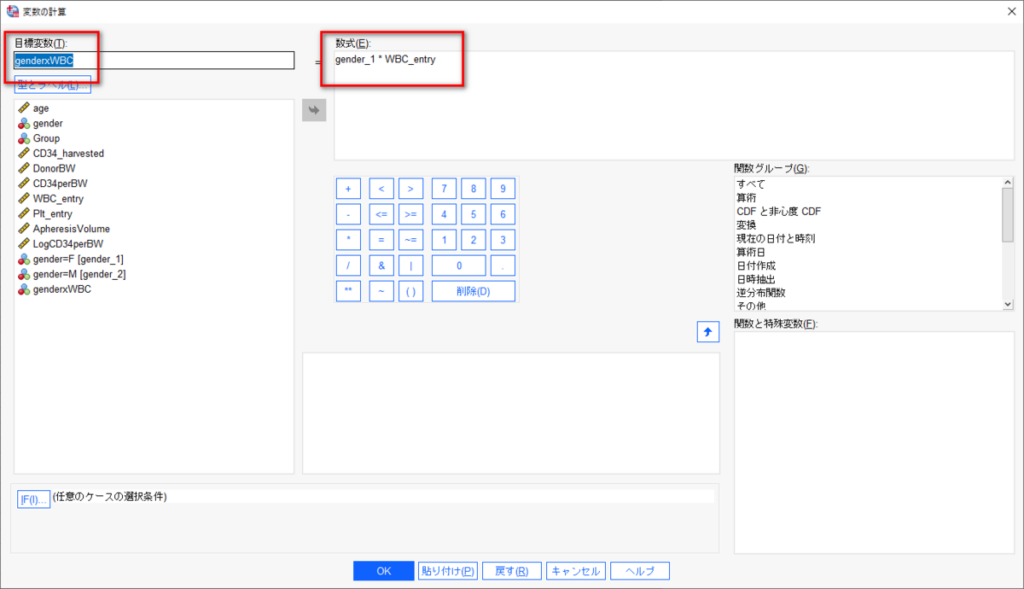
「変換」→「変数の計算」メニューで、交互作用項を作成する。
左赤枠のように、変数名を決めて、右赤枠のように計算式を書き入れる。
変数名や計算記号はいずれもダブルクリックやシングルクリックで、入力可能だ。
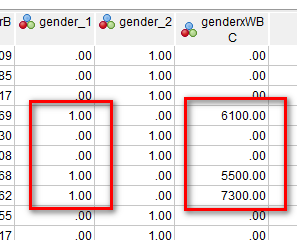
gender_1 は女性Fが１になっているダミー変数で、WBC_entry と掛け算すると、女性の WBC_entry だけ数値が残り、男性の値はゼロとなる変数ができる。
これが交互作用項である。
SPSSで交互作用項を含んだ重回帰分析を行う
「分析」→「回帰」→「線型」を選択する。
独立変数に、注目したい変数 (ここではWBC_entry)、共変量 (age, gender_1)、そして交互作用項 (genderxWBC) を投入する。
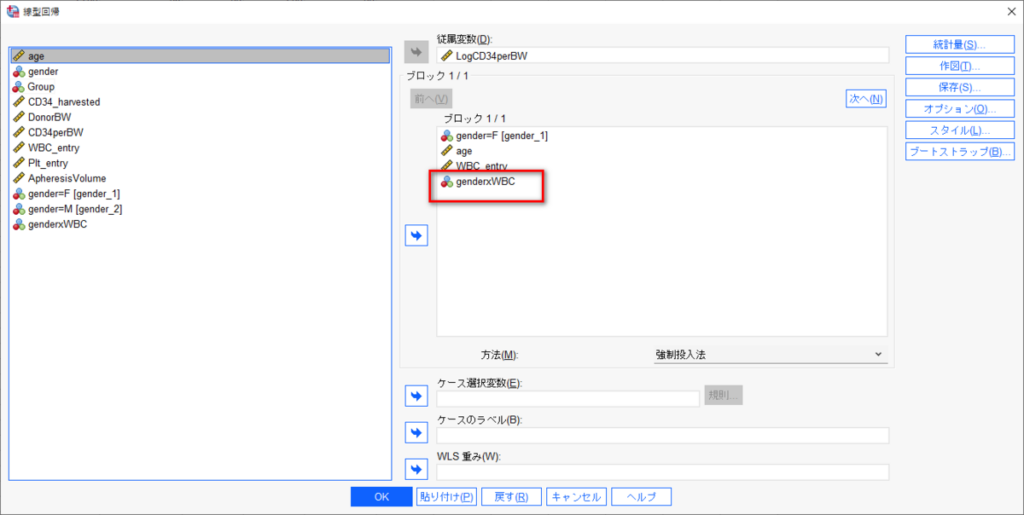
OKをクリックすると、結果が出力される。
SPSSの交互作用を含んだ重回帰分析の出力結果の読み方
係数という表を確認する。
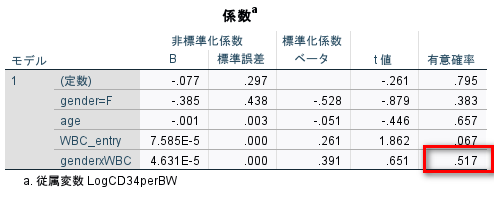
赤枠が、交互作用項の有意確率である。
帰無仮説は、「母集団の交互作用項の非標準化係数 B がゼロ」 である。
有意水準5％と考えると統計学的有意ではない。
交互作用項は有意水準を20％くらいにするという流儀もある。
それにしても統計学的有意ではない。
結論として、交互作用があるとは言えない。ということになる。
積極的に対処しないといけない交互作用はなさそうだ、くらいの解釈になる。
SPSSで交互作用を含んだ重回帰分析 一般線型モデルを用いる方法
実は、一般線型モデルを用いると、ダミー変数作成も、交互作用項作成も不要で便利だ。
いつもと違うメニューを使うのも全然問題ないという人は、こちらのやり方のほうが断然簡単だ。
「分析」→「一般線型モデル」→「１変量」を選択する。
先ほどと同じモデルにする場合、まず固定因子に gender を投入する。
共変量に age, WBC_entry を投入する。
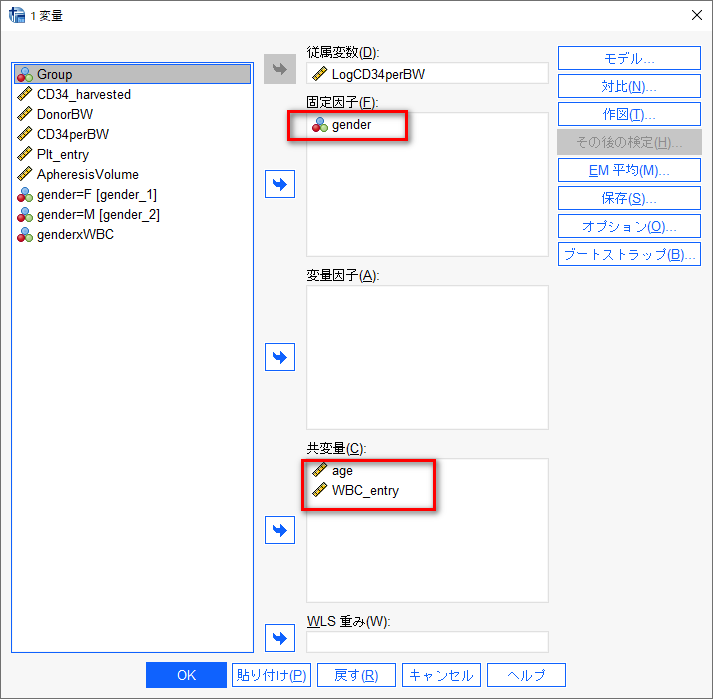
モデルをクリックする。
項の構築をクリック。
まず、age, gender, WBC_entry を主効果で投入する。
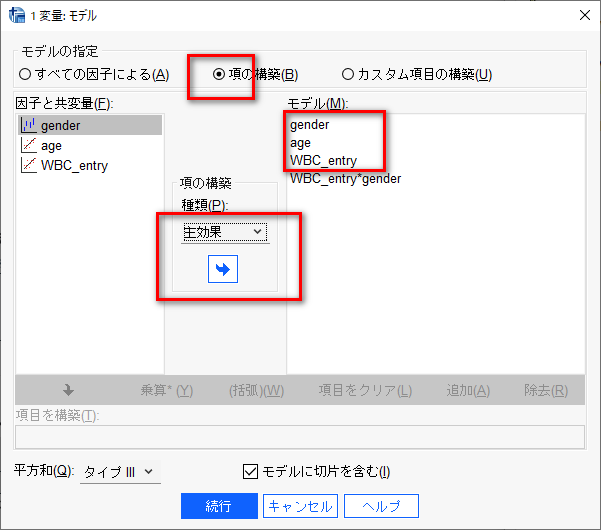
次に、左側の因子と共変量で gender と WBC_entry を選んで、交互作用で投入する。
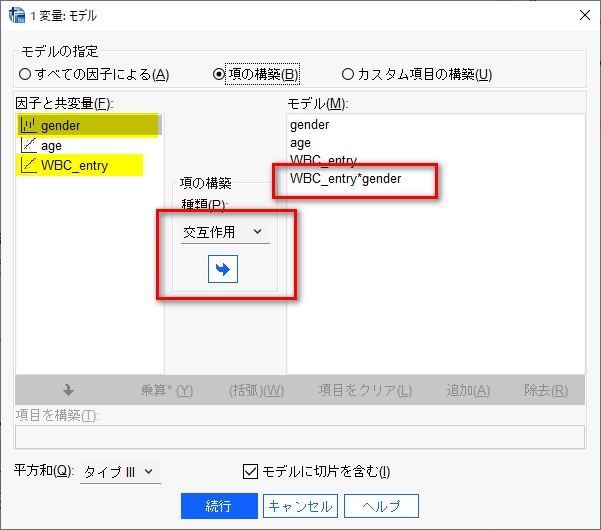
続行で戻る。
オプションで、パラメータの推定値にチェックを入れる。
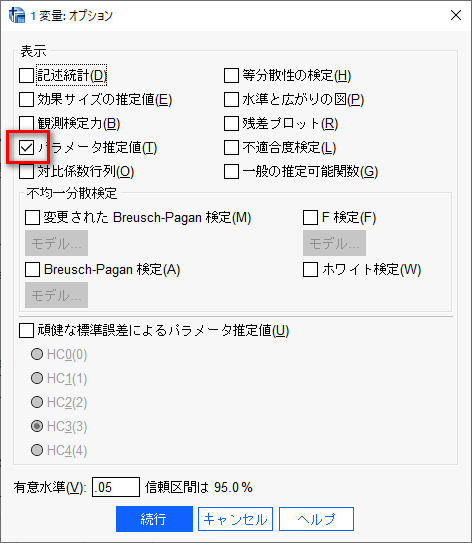
続行で戻り、OKで解析を実行する。
SPSSで交互作用を含んだ重回帰分析を一般線型モデルで実施した結果の見方
パラメータ推定値という表を見ると、交互作用項の有意確率が先ほどと同じ値で出力されているのがわかる。
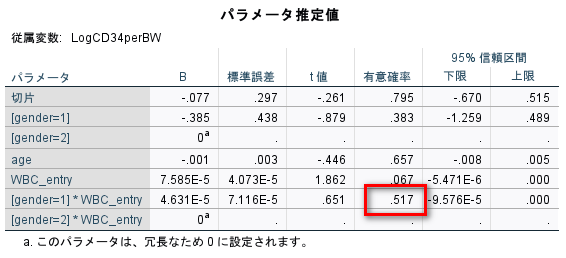
ちなみに、被験者間効果の検定という表でも同じ値が出力されているのがわかる。
こちらは、分散分析表だ。
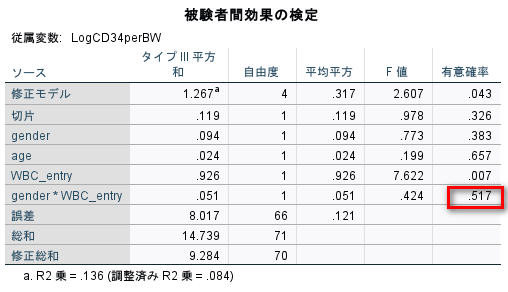
一般線型モデルのメニューのほうが、自動でダミー変数や交互作用項を作成してくれるので、とても簡単である。
カテゴリカルデータを含む重回帰分析はこちらのメニューのほうが便利である。
ただし、VIFを計算してくれないので、一長一短はある。
まとめ
SPSSの重回帰分析での交互作用項の作り方と解析の仕方を紹介した。
回帰→線型のメニューを使う場合、ダミー変数作成と交互作用項作成があるので少し面倒である。
一般線型モデルは、ダミー変数作成と交互作用項作成を、変数指定だけで自動で作成してくれるので、とても便利なメニューである。
メインは「回帰→線型」のメニューを使うとして、交互作用の確認にだけ、一般線型モデルを使用するという方法もあるかもしれない。
おすすめ書籍
SPSSで学ぶ医療系多変量データ解析 第2版
SPSSによる応用多変量解析
コメント