SPSS と GPower で重回帰分析に必要なサンプル数を計算する方法

重回帰分析を実施するのにサンプル数はどのくらい必要か？

ここでいうサンプル数とは、サンプルサイズのこと。

重回帰分析のサンプルサイズはどのように計算するのか？

重回帰分析の効果量とは何か？

重回帰分析のサンプル数計算に必要な値は？

サンプル数計算には、有意水準と検出力は必須項目である。

有意水準はαと呼び、たいていは0.05とする。

検出力は、1－βとも書かれることが多く、たいていは0.8とする。

これは慣例で決まっているので、基本はこれでよい。

では、それ以外に必要な値は何だろうか？

SPSSで計算する場合、重回帰モデルの重偏相関係数が必要になる。

重偏相関係数はいわゆるラージアール R である。

決定係数がR2乗と言われるが、その平方根である。

それ以外に必要な値は、説明変数の予測数である。

どのくらいの説明変数が必要になるか予想する必要がある。

重回帰分析のサンプル数計算をSPSSでやってみる

検出力 0.8（単一べき乗値とある枠に入力する） 、仮説値として母集団の重偏相関係数（決定係数 R² の平方根）を0.36とする。

モデルの総予測値数（説明変数の数）を10、検定予測値の数（検定する説明変数の数）を10とする。

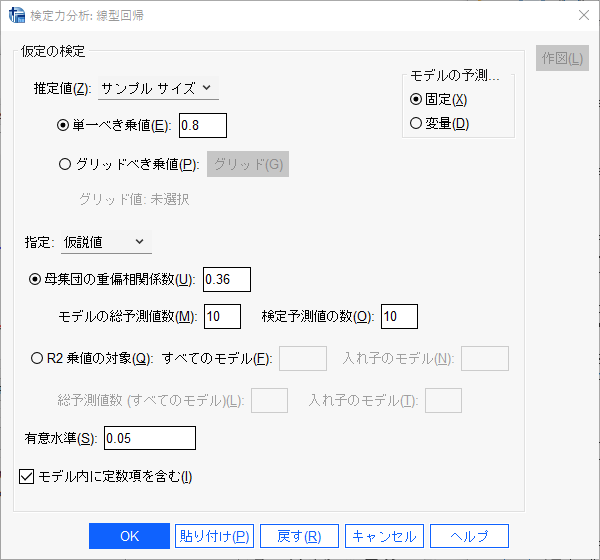
119例必要と計算される。

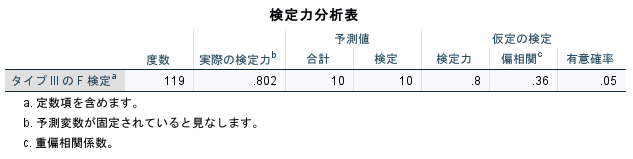
次に、指定のところの効果サイズを0.15とする。

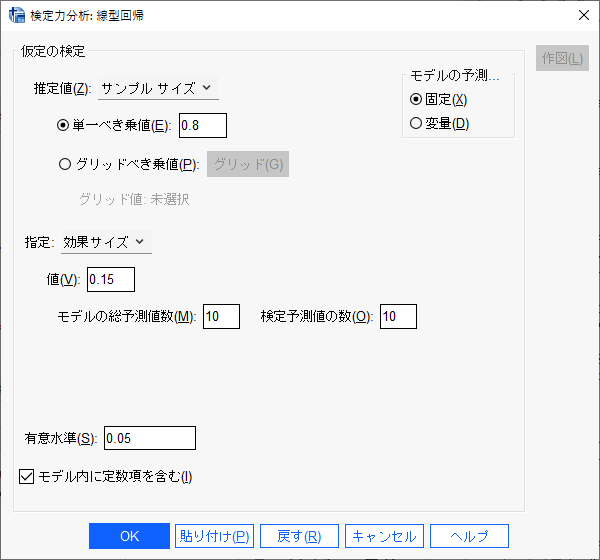
118例必要と計算される。

なぜほとんど同じ例数が必要と計算されるかというと、重偏相関係数 R と効果量 $ f^2 $ に以下の関係があるからだ。

$$ R^2 = \frac{f^2}{1 + f^2} $$

先ほどの数値を入れて計算すると、以下のようになる。

$$ \frac{0.15}{1 + 0.15} = 0.1304348 = 0.3611576^2 $$

つまり、効果量 0.15 と重偏相関係数0.36 はほぼ同義ということになる。

そのため、必要なサンプルサイズが同じ例数になる。

ちなみに、f²の計算式として変形すると以下のようになり、重偏相関係数 R（もしくは決定係数 R²）から効果量 f² が計算できる。

$$ f^2 = \frac{R^2}{1 – R^2} $$

重回帰分析の効果量は、このようにして決定係数から求められる。

重回帰分析のサンプル数計算をG*Powerで行うとどうなるか？

G*Powerは無料で使えるサンプルサイズ計算＆検出力計算に特化したソフトウェアだ。

以下のサイトからダウンロードできる。

Universität Düsseldorf: G*Power

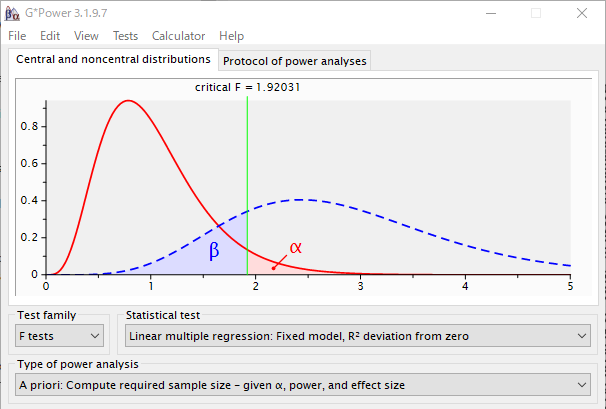
G*Powerで計算する場合、Test familyをF tests、Statistical testをLinear multiple regression: Fixed model, R² deviation from zeroを選択する。

Parameterは図の通り入れる。

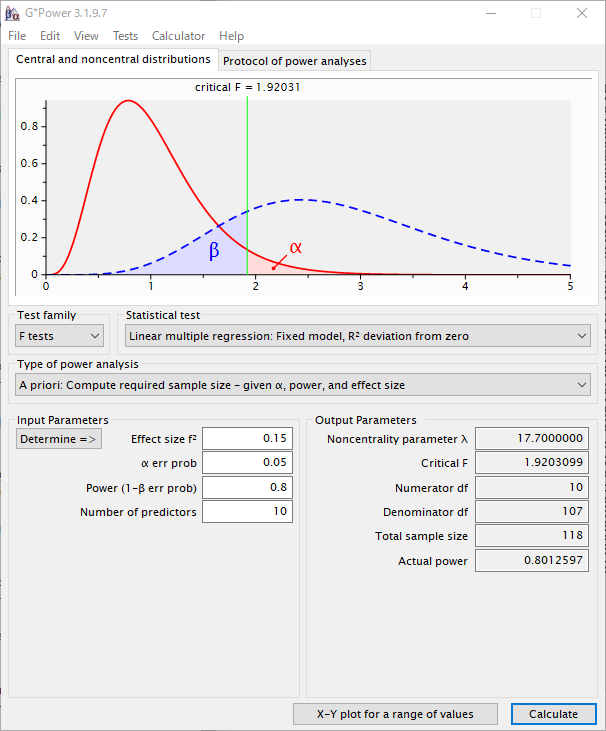
こちらも118例必要と計算された。

重回帰分析に説明変数がもっと必要な場合

検定する説明変数を15個に増やすと、139例必要と計算された。

G*Powerでも同じ計算結果であった。

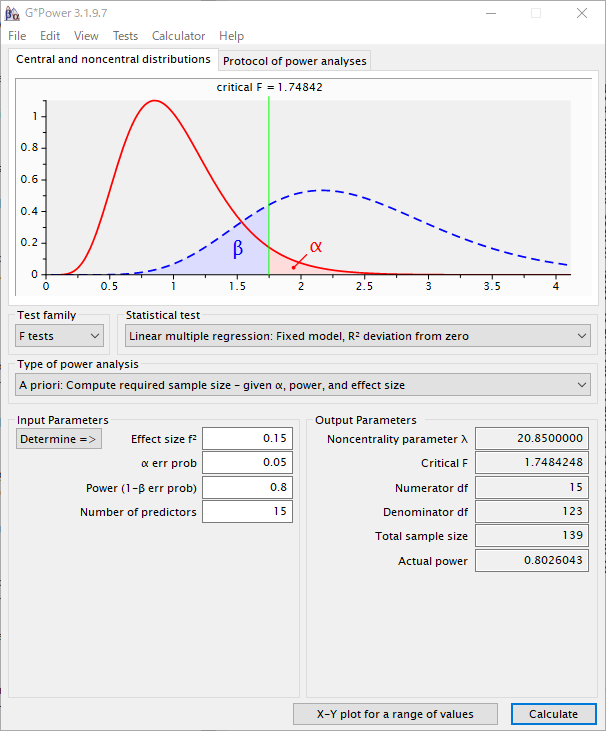
つまり、検定する説明変数が増えると、必要となるサンプルサイズは大きくなる。

重回帰分析の効果量に慣例的な目安がある

重偏相関係数や効果量がまったく見積もれない場合、慣例的に用いることができる効果量の目安がある。

• Small Effect Size: f² = 0.02 (R ≒ 0.14)
• Medium Effect Size: f² = 0.15 (R ≒ 0.36)
• Large Effect Size: f² = 0.35 (R ≒ 0.51)

全く予想がつかない場合は、これらの慣例を使うこともできる。

まとめ

重回帰分析の効果量とサンプルサイズ計算について紹介した。

事前に重偏相関係数と検定する説明変数の数の想定が必要である。

重偏相関係数から効果量が計算できる。

慣例の効果量の大きさを使うこともできる。

参考書籍

Jacob Cohen. Statistical Power Analysis for the Behavioral Sciences Second Edition.

https://www.utstat.toronto.edu/~brunner/oldclass/378f16/readings/CohenPower.pdf

PDF P.410あたりから