EZR のフィッシャーの正確検定で計算されるオッズ比の注意点

EZRのFisherの正確検定の関数でオッズ比を計算すると、通常の手計算で計算できるオッズ比と異なる数値が計算される。

これはなぜなのか？

EZRのFisherの正確検定を使わないオッズ比の計算

オッズ比は、通常は以下のような分割表だった場合、$ \frac{a/c}{b/d} $と計算する。

a=80, b=20, c=50, d=50だったとすれば、オッズ比は、$ \frac{80/50}{20/50} = 4 $ と計算される。

EZRのFisherの正確検定を使った場合のオッズ比の計算

EZR の Fisherの正確検定を使った場合、このオッズ比が以下のように3.97となる。これはいったいどういうことだろうか？

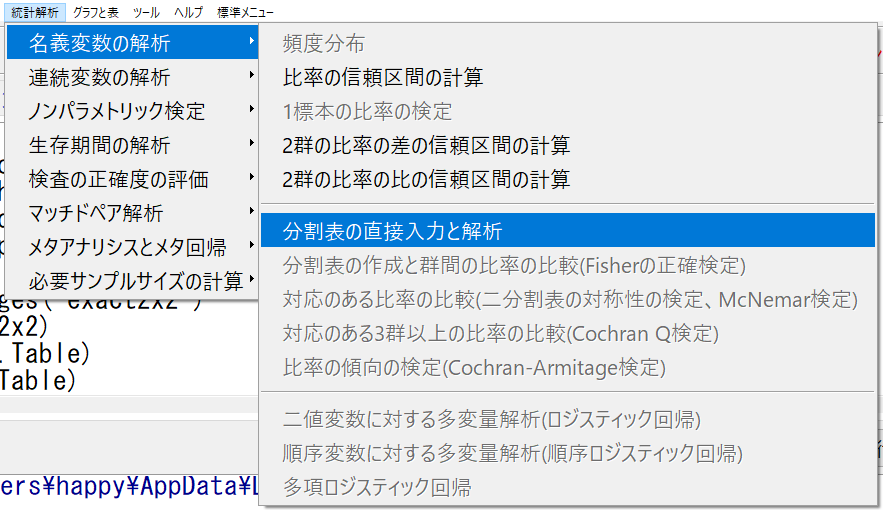
分割表に直接数値を入力しOKをクリック！

> fisher.test(.Table)
Fisher's Exact Test for Count Data
data:  .Table
p-value = 0.00001389
alternative hypothesis: true odds ratio is not equal to 1
95 percent confidence interval:
 2.049148 7.919959
sample estimates:
odds ratio 
  3.970815

EZRのFisherの正確検定で使っているオッズ比の計算方法

これは、EZRのFisherの正確検定で使っているオッズ比計算の方法が、単純なオッズ比計算とは異なるからだ。

条件付き最尤推定量（Conditional Maximum Likelihood Estimate）を計算しているので、サンプルから単純に計算するオッズ比と異なることになる。

通常計算する単純なオッズ比は、条件なしの最尤推定量（Unconditional Maximum Likelihood Estimate）で、このオッズ比はWaldのオッズ比とも呼ばれる。

今回の 2×2 のデータが得られたという条件で、最尤推定量を求めているのがFisherのオッズ比なのである。

三重大学名誉教授の奥村先生の説明はとてもわかりやすいので、ぜひ一読を。

下段の「オッズ比」というセクションが該当箇所。

https://okumuralab.org/~okumura/stat/fishertest.html

ちなみに、最尤推定量というのは、ある現象をモデル化し、（今回は 2×2 の分割表なので、二項分布でモデル化し、）得られたデータからそのモデルの尤度（もっともらしさ）が最大になるようにしたときのパラメータのことを言う。

その最尤推定量を求める際に、条件を付けたということ。

参考：尤度とは？

EZRでFisherのオッズ比でないオッズ比を求めるには？

epitools パッケージをインストールして、oddsratio.wald() を使うとよい。

Rスクリプトの窓に以下のように書いて、インストールして、パッケージを使えるようにする。

install.packages("epitools") #一回のみ。実行するとパッケージデータを取得するサーバーを選ぶ窓が開くのでJapanを選択。
library(epitools) #パッケージ使用時に事前に一回実行。

先ほどの結果を一部流用して、Waldのオッズ比（通常のオッズ比）を計算してみると以下のようになる。

odds ratioとある個所のestimateが４になっているのがわかる。

> oddsratio.wald(.Table)
$data
1  2 Total
1      80 20   100
2      50 50   100
Total 130 70   200
$measure
NA
odds ratio with 95% C.I. estimate    lower   upper
1        1       NA      NA
2        4 2.135711 7.49165
$p.value
NA
two-sided   midp.exact  fisher.exact     chi.square
1           NA            NA             NA
2 0.0000085777 0.00001388917 0.000008687712
$correction
[1] FALSE
attr(,"method")
[1] "Unconditional MLE & normal approximation (Wald) CI"

このパッケージを使って、Fisherのオッズ比を計算してみる場合は、oddsratio.fisher() を使う。

fisher.test() と同じ結果であることがわかる。

> oddsratio.fisher(.Table)
$data
1  2 Total
1      80 20   100
2      50 50   100
Total 130 70   200
$measure
NA
odds ratio with 95% C.I. estimate    lower    upper
1 1.000000       NA       NA
2 3.970815 2.049148 7.919959
$p.value
NA
two-sided   midp.exact  fisher.exact     chi.square
1           NA            NA             NA
2 0.0000085777 0.00001388917 0.000008687712
$correction
[1] FALSE
attr(,"method")
[1] "Conditional MLE & exact CI from 'fisher.test'"

まとめ

EZRで、Fisherの正確検定を使ってオッズ比を計算すると、手計算で行ったオッズ比と異なる数値が示されるが、それはなぜかという話をした。

通常の手計算でできるオッズ比は、条件なしの最尤推定量（Unconditional Maximum Likelihood Estimate）であり、fisher.test()で計算されるオッズ比は、条件付き最尤推定量（Conditional Maximum Likelihood Estimate）であるため、数値が異なる。

どちらを使っているかを断れば、どちらを使っても間違いではないと言える。

参考サイト

https://okumuralab.org/~okumura/stat/fishertest.html