R で時系列データの自己相関を計算する方法

自己相関を時系列データで計算する方法を解説した。

時系列データとは？

時系列データは、時間とともに計測したデータのこと。

毎日のデータ、毎月のデータ、四半期のデータ、毎年のデータというような定期的な時間で取得したデータのこと。

このデータを分析することで、データ変化の傾向を見ることができる。

毎日の株価、為替レートとか、毎年の成人喫煙率なんかも時系列データ。

自己相関を時系列データで計算する

Rには acf() という関数があり、この関数で自己相関を計算できる。

自己相関とは、時系列データを分析する方法の一つで、例えば、ある日のデータと次の日のデータ、またある日のデータとその次の日のデータという組み合わせを作ったうえでの相関係数を計算したもの。

相関係数を計算するデータ同士は、翌日だけでなく、ある日と翌々日でもいいし、ある日と三日後でもいい。そういう間隔で相関係数を計算するというもの。

Rの例として、ldeathsというデータがある。これは1974年から1979年のイギリスのデータで、気管支炎、肺気腫、喘息で亡くなった人の月ごとの人数のデータである。

どんなデータか表示してみると以下の通り。

> ldeaths
Jan  Feb  Mar  Apr  May  Jun  Jul  Aug  Sep  Oct  Nov  Dec
1974 3035 2552 2704 2554 2014 1655 1721 1524 1596 2074 2199 2512
1975 2933 2889 2938 2497 1870 1726 1607 1545 1396 1787 2076 2837
1976 2787 3891 3179 2011 1636 1580 1489 1300 1356 1653 2013 2823
1977 3102 2294 2385 2444 1748 1554 1498 1361 1346 1564 1640 2293
1978 2815 3137 2679 1969 1870 1633 1529 1366 1357 1570 1535 2491
1979 3084 2605 2573 2143 1693 1504 1461 1354 1333 1492 1781 1915

行はある年の月別の死亡者数、列は毎年のある月の死亡者数、というふうに並んでいる。

このデータを使って、自己相関を計算してみる。

計算するスクリプトはとても簡単。

acf(ldeaths)

デフォルトでは図で表示されるのみになっている。

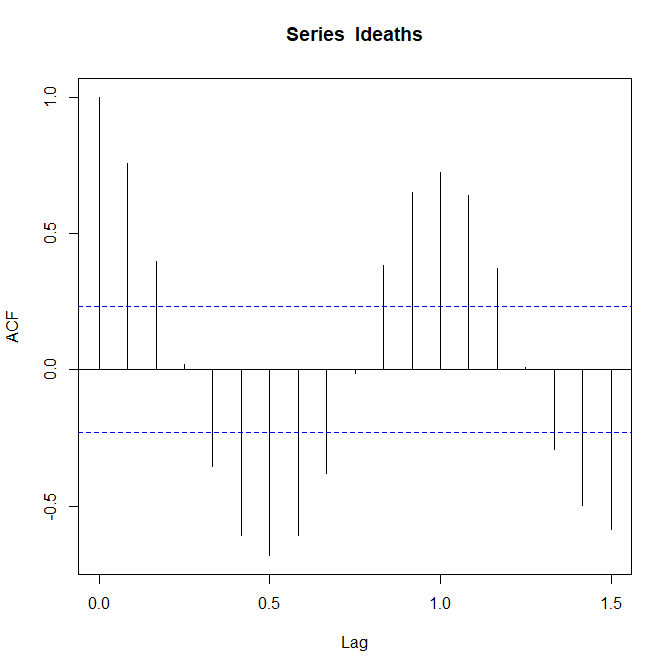
縦軸が自己相関の値。通常の相関係数と同じく、-1から1が範囲になっている。1が正の相関Max、-1が負の相関Max。

横軸はLagとあるが、これがいくつのズレかというもの。

1は1年で、その間に12個縦棒がある。順番に0か月ずれ（同じ値）、1か月ずれ、2か月ずれ、、、となっている。なぜ、1か月、2か月が1,2となっていないのかは、次を見ればわかる。次は自己相関の値を表示させてみる。

acf(ldeaths, plot=FALSE)

plot=FALSEというオプションをつけると以下が出力される。

> acf(ldeaths,plot=FALSE)
Autocorrelations of series ‘ldeaths’, by lag
0.0000 0.0833 0.1667 0.2500 0.3333 0.4167 0.5000 0.5833 0.6667
1.000  0.755  0.397  0.019 -0.356 -0.609 -0.681 -0.608 -0.378
0.7500 0.8333 0.9167 1.0000 1.0833 1.1667 1.2500 1.3333 1.4167
-0.013  0.383  0.650  0.723  0.638  0.372  0.009 -0.294 -0.497
1.5000
-0.586

0.0000, 0.0833, 0.1667, 0.2500, …となっているのは、1/12=0.0833だからだ。1か月が0.0833と計算されていて、12か月は12/12=1となっている。

これがLagとしてプロットされている。これでLagの1,2が、1か月、2か月ではないことがわかるだろう。

自己相関の図を見てみると、Lagが0.5のときが一番強い負の相関で、1のときが一番強い正の相関がある。

これはもともとのデータをプロットしてみると、納得がいく。

plot(ldeaths)

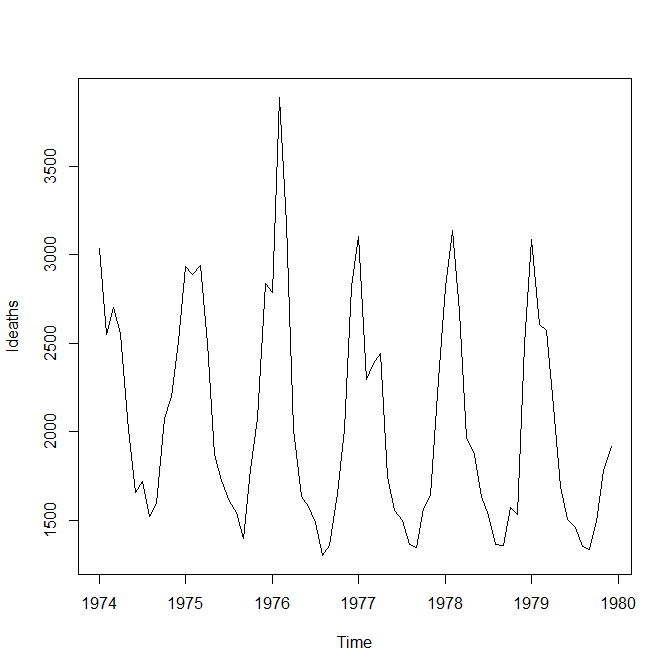
この経年変化の図を見るとわかるが、年の初めと終わりにピークが来ていて、年の真ん中に底がある。

これは、冬に呼吸器疾患で亡くなる人が多く、夏には少ないという傾向を示している。

呼吸器にリスクを抱えている人は、冬の感染症の季節には亡くなるリスクが高くなるというわけだ。

この関係を呼吸器疾患による死亡者数というデータの自己相関解析で改めて示した形になる。

このようにデータで示されると説得力が増す。

自己相関を計算するときは時系列データへの変換が必要

気を付けなければいけないのは、時系列データ解析をRで行うときには、まず時系列データへの変換が必要であることだ。

ldeaths は、時系列データ（time series）に変換されているデータなので簡単に扱えた。

> str(ldeaths)
Time-Series [1:72] from 1974 to 1980: 3035 2552 2704 2554 2014 ...

通常のデータは時系列データに変換してから使わないといけない。

例えば、ドル円為替レートのデータで、時系列データへの変換と自己相関解析をしてみよう。

過去記事のデータを使ってみる。

まずデータを読み込む。

Windowsのドキュメントフォルダにdataフォルダを作りその中にCSVデータを入れる。

dat <- read.csv("data/tm_quote.csv")

このデータは2020年の年始の14営業日の円の為替レートである。

ドル円のデータだけを取り出してみてみる。

> dat[,1:2]
X    USD
1   2020/1/6 108.12
2   2020/1/7 108.45
3   2020/1/8 107.85
4   2020/1/9 109.25
5  2020/1/10 109.55
6  2020/1/14 110.16
7  2020/1/15 109.95
8  2020/1/16 109.96
9  2020/1/17 110.33
10 2020/1/20 110.19
11 2020/1/21 110.24
12 2020/1/22 109.91
13 2020/1/23 109.72
14 2020/1/24 109.59

このdatの中の、USDを時系列データに変換する。ts()という関数を使う。

ts.usd <- ts(dat[,2])

ts.usdを確認してみると以下のようになっている。

これで時系列データに変換できた。

> ts.usd
Time Series:
Start = 1
End = 14
Frequency = 1
[1] 108.12 108.45 107.85 109.25 109.55 110.16 109.95 109.96 110.33 110.19 110.24 109.91 109.72 109.59
> str(ts.usd)
Time-Series [1:14] from 1 to 14: 108 108 108 109 110 ...

ここで、プロットしてみて、自己相関係数の図も描いてみる。

さらに自己相関係数の数値を出力してみる。

plot(ts.usd)
acf(ts.usd)
acf(ts.usd,plot=FALSE)

単なるプロットでは傾向は見えてこない。

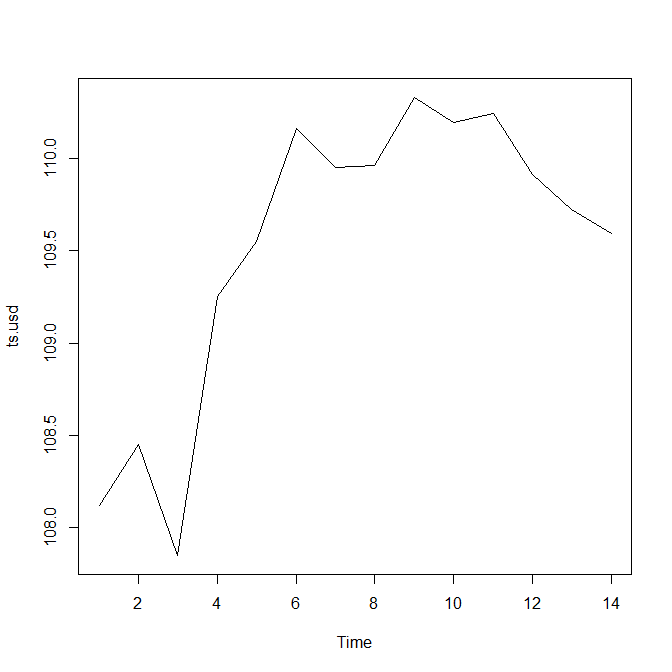
自己相関は8営業日間隔に向かって、どんどん逆相関に向かっている傾向が見える。

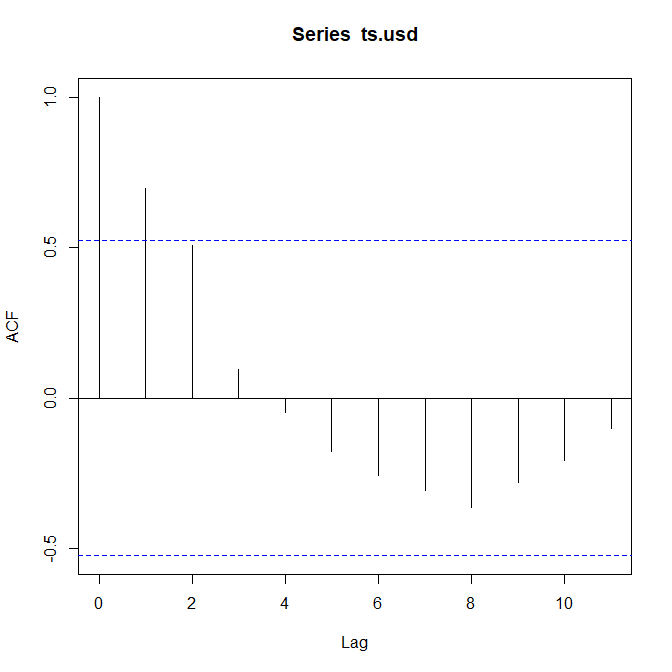
自己相関の解析結果は、以下のとおり。

> plot(ts.usd)
> acf(ts.usd)
> acf(ts.usd,plot=FALSE)
Autocorrelations of series ‘ts.usd’, by lag
0      1      2      3      4      5      6      7      8      9
1.000  0.696  0.508  0.093 -0.049 -0.177 -0.259 -0.306 -0.362 -0.281
10     11
-0.208 -0.103

実際には、14日営業日だけのデータでは少なすぎるため、もっとたくさんのデータを用いたほうが、より強固な解析結果になると思う。

まとめ

時系列データとは何かを簡単に説明した。

時系列データの自己相関をRで計算してみた。

時系列データ解析の前には、時系列データへの変換が必要で、その方法を解説した。

関連記事

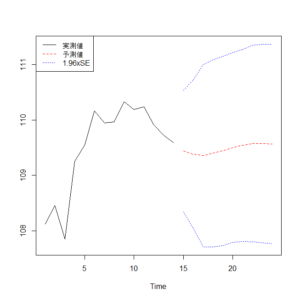
以下の記事では、未来予測まで行っている。よければこちらもどうぞ。