医療研究や社会調査など、さまざまな分野のデータ解析で登場する固定効果と変量効果。これらは、データを回帰モデルで分析する際に、「集団全体の平均的な傾向」と「個々の対象が持つ固有のばらつき」をどのように扱うか、という考え方に基づいている。
固定効果:集団の「平均的な効果」を推定する
まず固定効果について。これは、データから集団全体の平均的な傾向や効果を推定する際に用いられる考え方である。
たとえば、ある薬の効果を検証する臨床試験を考えてみる。多くの患者さんに薬を投与し、その効果を評価する。このとき、私たちは「この薬は一般的にどのくらいの効果があるのか?」という、患者さん全体の平均的な効果を知りたいと考えるはずである。
これは、私たちが普段よく使う重回帰分析、ロジスティック回帰分析、Cox回帰分析といった統計モデルの基本的な考え方である。これらのモデルでは、対象となるすべてのデータポイントをまとめて、「平均的にはどうなのか」という視点で分析を進める。個々の患者さんの特性(例えば、元々の病状の重さや年齢など)は、共変量としてモデルに組み込むことで、その影響を調整しながら、薬の「平均的な効果」を推定している。
通常、これらのモデルでは「固定効果」という言葉をあえて使わないことが多いが、これは個々の対象のばらつきではなく、集団としての平均的な効果を推定している。データが1回しか測定されていない場合(例えば、治療前と治療後の差を1つのデータとして扱う場合なども含む)は、この固定効果のみを考慮することになる。
変量効果:個人の「固有のばらつき」を考慮する
次に、変量効果を考える。これは、同じ対象から複数回データが測定されるような場合に、個々の対象が持つ固有のばらつき(個人差)を考慮するための考え方である。
先ほどの薬の例で考えてみよう。もし患者さんの経過を複数回(例えば、治療開始後1ヶ月、3ヶ月、6ヶ月といった具合に)測定できるとしたらどうだろうか?
ある患者さんはもともと血圧が高めなので、治療後も平均より高い値で推移するかもしれない。別の患者さんはもともと低めなので、治療後も平均より低い値で安定するかもしれない。このように、患者さん一人ひとりに固有の傾向や「基準点」のようなものがあることが考えられる。これが個人差である。
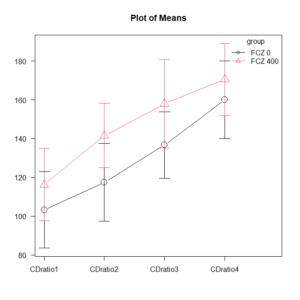
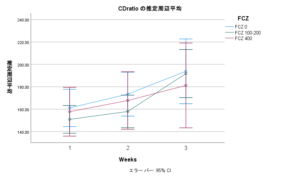
変量効果モデル(あるいは混合効果モデルとも呼ばれます)では、この個人差を「変量効果」としてモデルに組み込む。つまり、「この人はもともと平均より〇〇な傾向がある」という個人の特性を考慮した上で、それでもなお薬が「平均的にはどういう効果をもたらすのか(固定効果)」を推定するのである。
変量効果を考慮することで、単一時点の測定では見落とされがちな「たまたま出た値」ではなく、「その人の傾向」を踏まえた上で、より信頼性の高い分析が可能になる。個々の患者さんの背景にあるばらつきを適切にモデルに組み込むことで、より精度の高い「平均的な効果」を導き出すことができるのである。
メリットとデメリット
変量効果を考慮したモデルの最大のメリットは、データが示す「真の姿」をより正確に捉えられる点にある。複数回の測定から個人の傾向を把握できるため、単一の測定では見過ごされてしまうような、たまたま生じた誤差の影響を受けにくくなる。これにより、より信頼性の高い結果を得ることができ、介入の効果や要因の影響をより正確に評価できる。
一方で、デメリットもある。変量効果を考慮したモデルは、その計算方法や結果の解釈が、固定効果のみのモデルに比べて複雑になる傾向がある。また、複数回の測定が必要となるため、データ収集に手間やコストがかかる場合もある。
まとめ
このように、固定効果と変量効果は、データの性質や研究の目的に応じて使い分けられる。どちらのモデルが適切かは、「どのようなデータを、どのように捉えたいのか」という問いによって決まる。これらの概念を理解することで、データからより深い洞察を得るための選択肢が広がるだろう。





コメント