R に組み込みのタイタニック号の生存・死亡データで、生存・死亡に関するロジスティック回帰分析と、独立変数の多重比較を実行してみる。
- 解析するタイタニック号の生存・死亡データの確認
- 客室クラス間の生存・死亡の傾向（トレンド）
- 客室クラスに性別を加えたモデルで多重ロジスティック回帰分析もしてみる
- 別のタイタニック号データをサンプルデータとして使う
- まとめ
解析するタイタニック号の生存・死亡データの確認
解析するデータは、carData パッケージの TitanicSurvival というデータ。
carData パッケージは最初からインストールされているので、library() で呼び出すだけで使えるようになる。
library(carData) str(TitanicSurvival) summary(TitanicSurvival)
タイタニック号が沈没したときの生存・死亡（survived）、乗客の性別（sex）、年（age）、客室クラス（passengerClass）のデータである。
> str(TitanicSurvival) 'data.frame': 1309 obs. of 4 variables: $ survived : Factor w/ 2 levels "no","yes": 2 2 1 1 1 2 2 1 2 1 ... $ sex : Factor w/ 2 levels "female","male": 1 2 1 2 1 2 1 2 1 2 ... $ age : num 29 0.917 2 30 25 ... $ passengerClass: Factor w/ 3 levels "1st","2nd","3rd": 1 1 1 1 1 1 1 1 1 1 ... > summary(TitanicSurvival) survived sex age passengerClass no :809 female:466 Min. : 0.1667 1st:323 yes:500 male :843 1st Qu.:21.0000 2nd:277 Median :28.0000 3rd:709 Mean :29.8811 3rd Qu.:39.0000 Max. :80.0000 NA's :263
客室クラス間の生存・死亡の傾向（トレンド）
割合のグラフでトレンドを眺める
生存が、客室クラスの違いで傾向があるかどうかを見てみる。
(tab <- with(TitanicSurvival, table(passengerClass, survived))) prop.table(tab,1) prop.table(tab,1)[,2]*100 barplot(prop.table(tab,1)[,2]*100, xlab="Passenger Class", ylab="Survived (%)")
1309名中、客室クラス別乗客は一等が323名、二等が277名、三等が709名だった。
生存したのは500名だった。
一等が62%、二等が43%、三等が26%だった。
> (tab <- with(TitanicSurvival, table(passengerClass, survived))) survived passengerClass no yes 1st 123 200 2nd 158 119 3rd 528 181 > > prop.table(tab,1) survived passengerClass no yes 1st 0.3808050 0.6191950 2nd 0.5703971 0.4296029 3rd 0.7447109 0.2552891 > > prop.table(tab,1)[,2]*100 1st 2nd 3rd 61.91950 42.96029 25.52891
グラフにすると見事に傾向（トレンド）がみられる。
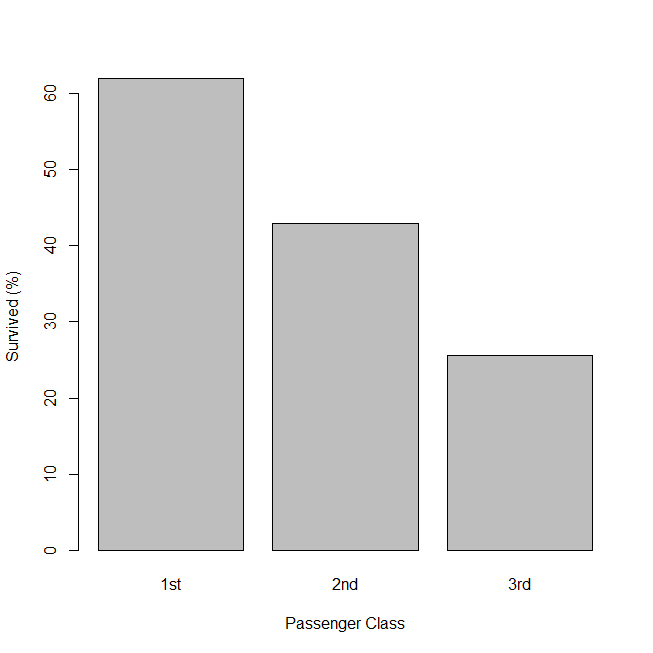
単変量ロジスティック回帰分析
まず、glm()とfamily=binomialの組み合わせでロジスティック回帰分析を行う。
glm.res <- glm(survived ~ passengerClass, family=binomial(), data=TitanicSurvival) summary(glm.res)
二等（passengerClass2nd）も三等（passengerClass3rd）も生存オッズ比は一等に比べ低い（ログオッズでマイナス）と計算された。
> summary(glm.res) Call: glm(formula = survived ~ passengerClass, family = binomial(), data = TitanicSurvival) Deviance Residuals: Min 1Q Median 3Q Max -1.3896 -0.7678 -0.7678 0.9791 1.6525 Coefficients: Estimate Std. Error z value Pr(>|z|) (Intercept) 0.4861 0.1146 4.242 2.21e-05 *** passengerClass2nd -0.7696 0.1669 -4.611 4.02e-06 *** passengerClass3rd -1.5567 0.1433 -10.860 < 2e-16 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 (Dispersion parameter for binomial family taken to be 1) Null deviance: 1741.0 on 1308 degrees of freedom Residual deviance: 1613.3 on 1306 degrees of freedom AIC: 1619.3 Number of Fisher Scoring iterations: 4
対数を真数に直すとよりわかりやすい。
自前のrr.95ci()を使う。
rr.95ci <- function(x){ res <- exp(cbind(coef(x),confint(x))) colnames(res) <- c("RR","LL(2.5%)","UL(97.5%)") round(res,2) } rr.95ci(glm.res)
二等は生存オッズ比 0.46、三等は生存オッズ比 0.21であった。
１より低い値は、生き残れなかったことを意味する。
> rr.95ci(glm.res) Waiting for profiling to be done... RR LL(2.5%) UL(97.5%) (Intercept) 1.63 1.30 2.04 passengerClass2nd 0.46 0.33 0.64 passengerClass3rd 0.21 0.16 0.28
トレンド検定（傾向性の検定）をしてみる
glm()の結果を利用して、トレンド検定をしてみる。
multcomp パッケージのglht()を使って行う。
multcomp パッケージを使うには、事前にインストールしておく。
glht は genral linear hypothesisの略。
install.packages("multcomp")
使うときはlibrary()で呼び出して使う。
library(multcomp)
トレンドの対比（コントラスト Contrast）を作成しておく。
特段思うところがなければ線形に。
今回のように、一等、二等、三等などの3つのカテゴリなら（1,0,-1）がいい。
トレンド対比のコントラストは、合計をゼロにするのが条件で、なるべく恣意性（しいせい）をなくした対比にするなら、カテゴリ間の間隔が等しい（今回は1）ものがよい。
4つの場合は (-3, -1, 1, 3)、5つの場合は (-2, -1, 0, 1, 2) などがよい。
glht()に、glm()の結果を投入し、線形関数 linear function (linfct) に 多重比較 multiple comparison (mcp) を選択し、その比較変数とコントラストを、mcp(passengerClass = contr) というふうに指定する。
contr <- rbind("linear trend" = c(1,0,-1))
glht.res <- glht(glm.res, linfct = mcp(passengerClass = contr))
summary(glht.res)
結果はこちら。
> summary(glht.res) Simultaneous Tests for General Linear Hypotheses Multiple Comparisons of Means: User-defined Contrasts Fit: glm(formula = survived ~ passengerClass, family = binomial(), data = TitanicSurvival) Linear Hypotheses: Estimate Std. Error z value Pr(>|z|) linear trend == 0 1.5567 0.1433 10.86 <2e-16 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 (Adjusted p values reported -- single-step method)
linear trend==0 の行がトレンド検定の結果で、右端のp値を見ると、統計学的有意であることがわかる。
Estimateを見ると、ロジスティック回帰の結果と同じ絶対値の 1.5567 だ。
ロジスティック回帰の見るべき行は、三等の生存オッズ比のEstimateだ。
符号が異なるが絶対値は同じ値であることがわかる。
つまり、三群の場合のトレンド検定は、最小の群と最大の群の比較と言えるわけだ。
客室クラスに性別を加えたモデルで多重ロジスティック回帰分析もしてみる
2つ以上の変数を投入しても解析できる。glm()に「+」で変数を追加するだけだ。
glm.res2 <- glm(survived ~ sex + passengerClass, data=TitanicSurvival, family=binomial) glht.res2 <- glht(glm.res2, linfct = mcp(passengerClass = contr)) summary(glm.res2) summary(glht.res2)
男性の生存ログオッズが計算されているが、マイナス値であり、女性に比べて生存しなかったことがわかる。
客室クラスの値は単変量のときと大差なし。
客室クラスの生存オッズ比のトレンド検定の結果も単変量と同様に統計学的有意であった。
> summary(glm.res2) Call: glm(formula = survived ~ sex + passengerClass, family = binomial, data = TitanicSurvival) Deviance Residuals: Min 1Q Median 3Q Max -2.1089 -0.6984 -0.4741 0.7167 2.1173 Coefficients: Estimate Std. Error z value Pr(>|z|) (Intercept) 2.1091 0.1728 12.203 < 2e-16 *** sexmale -2.5150 0.1467 -17.145 < 2e-16 *** passengerClass2nd -0.8808 0.1977 -4.456 8.34e-06 *** passengerClass3rd -1.7231 0.1715 -10.047 < 2e-16 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 (Dispersion parameter for binomial family taken to be 1) Null deviance: 1741.0 on 1308 degrees of freedom Residual deviance: 1257.2 on 1305 degrees of freedom AIC: 1265.2 Number of Fisher Scoring iterations: 4 > summary(glht.res2) Simultaneous Tests for General Linear Hypotheses Multiple Comparisons of Means: User-defined Contrasts Fit: glm(formula = survived ~ sex + passengerClass, family = binomial, data = TitanicSurvival) Linear Hypotheses: Estimate Std. Error z value Pr(>|z|) linear trend == 0 1.7231 0.1715 10.05 <2e-16 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 (Adjusted p values reported -- single-step method)
別のタイタニック号データをサンプルデータとして使う
タイタニック号のデータは、datasets パッケージにもある。名前は Titanic データ。
こちらの記事も参照。
https://toukeier.hatenablog.com/entry/2019/09/10/213649toukeier.hatenablog.com
Titanic データは、乗務員のデータも含まれていて、データ行が多い。
客室クラスの人数も若干異なる（がほとんど同じ）。
> rowSums(apply(Titanic,c(1,4),sum)) 1st 2nd 3rd Crew 325 285 706 885 > summary(TitanicSurvival$passengerClass) 1st 2nd 3rd 323 277 709
Titanic データで Class の生存オッズ比の多重比較をしてみる。
乗務員は序列がつかず、トレンドに組み込みにくい。
ゆえに、多重比較コントラストはTukeyにする。
Tukeyは総当たりの方法だ。
Tukeyはこちらも参照のこと。
Titanicデータは、as.data.frame()でデータフレームに変換してから、人数集計データゆえのweights=Freqオプションを使う方法で解析する。
客室クラス・乗務員の群分けと生存・死亡の多重比較を、単変量モデルと性別、年齢（大人か子供か）も考慮に入れた多変量で検討してみる。
dat <- as.data.frame(Titanic) logi1 <- glm(Survived~Class,weights=Freq,data=dat,family=binomial) logi2 <- glm(Survived ~ Class+Sex+Age, weights=Freq, family=binomial, data=dat) summary(glht(logi1, linfct = mcp (Class = "Tukey"))) summary(glht(logi2, linfct = mcp (Class = "Tukey")))
単変量解析の総当たり比較の結果、三等客室の乗客と乗務員が同じで、あとはすべて統計学的有意に異なるという結果だった。
性別と大人・子供を考慮すると二等の乗客と乗務員が同じという結果に変わった。
> summary(glht(logi1, linfct = mcp (Class = "Tukey"))) Simultaneous Tests for General Linear Hypotheses Multiple Comparisons of Means: Tukey Contrasts Fit: glm(formula = Survived ~ Class, family = binomial, data = dat, weights = Freq) Linear Hypotheses: Estimate Std. Error z value Pr(>|z|) 2nd - 1st == 0 -0.85649 0.16609 -5.157 <1e-05 *** 3rd - 1st == 0 -1.59650 0.14365 -11.114 <1e-05 *** Crew - 1st == 0 -1.66434 0.13902 -11.972 <1e-05 *** 3rd - 2nd == 0 -0.74000 0.14824 -4.992 <1e-05 *** Crew - 2nd == 0 -0.80785 0.14375 -5.620 <1e-05 *** Crew - 3rd == 0 -0.06785 0.11711 -0.579 0.937 --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 (Adjusted p values reported -- single-step method) > summary(glht(logi2, linfct = mcp (Class = "Tukey"))) Simultaneous Tests for General Linear Hypotheses Multiple Comparisons of Means: Tukey Contrasts Fit: glm(formula = Survived ~ Class + Sex + Age, family = binomial, data = dat, weights = Freq) Linear Hypotheses: Estimate Std. Error z value Pr(>|z|) 2nd - 1st == 0 -1.0181 0.1960 -5.194 <1e-04 *** 3rd - 1st == 0 -1.7778 0.1716 -10.362 <1e-04 *** Crew - 1st == 0 -0.8577 0.1573 -5.451 <1e-04 *** 3rd - 2nd == 0 -0.7597 0.1764 -4.308 <1e-04 *** Crew - 2nd == 0 0.1604 0.1738 0.923 0.791 Crew - 3rd == 0 0.9201 0.1486 6.192 <1e-04 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 (Adjusted p values reported -- single-step method)
まとめ
タイタニック号の生存・死亡データを用いて、客室クラスの違いによる生存確率を検討した。
一等、二等、三等の順に生存できなかったトレンドが見られた。
生存・死亡など二値のデータを扱う回帰分析は、ロジスティック回帰分析で、R ではglm()を使い、familiy=binomialという指定を入れる。
また、モデル中の三群以上のトレンド検定を行いたいときは、glm()の結果を用いて、multcomp パッケージのglht()を使うとよい。
トレンド対比は (-1, 0, 1), (-3, -1, 1, 3), (-2, -1, 0, 1, 2) などを使う。
もう一つのタイタニック号のデータ Titanic で、ロジスティック回帰分析＆多重比較を行ってみた。
multcomp パッケージの glht()を使うと、多変量調整のモデル中のグループ変数における三群以上の多重比較ができる。
コメント