ブートストラップ法で平均値の95%信頼区間を求めよう！

---

「このデータ、本当に信頼できるのか？」そう思ったことはないだろうか。限られたデータから全体像を推測する際、統計的な「信頼区間」は非常に重要な概念である。しかし、信頼区間を算出するには、データの分布に特定の仮定が必要となるケースが少なくない。

そこで今回は、そんな仮定に縛られず、もっと柔軟に信頼区間を推定できる「ブートストラップ法」を紹介する。特に、平均値の95%信頼区間を求める方法に焦点を当て、具体的な手順からRを使った計算例、そして結果の解釈までを分かりやすく解説する。

---

概要

ブートストラップ法は、手元にあるデータから繰り返しリサンプリング（復元抽出）を行うことで、元のデータの分布に関する仮定を置くことなく、推定量の標本分布を近似し、信頼区間を推定するノンパラメトリックな統計的手法である。

平均値の95%信頼区間をブートストラップ法で求める基本的な手順は以下の通りである。

1. 元のデータセットから復元抽出で新しいデータセットを生成する：元のデータセットと同じサイズのデータセットを、重複を許して（復元抽出）生成する。
2. 新しいデータセットの平均値を計算する：生成された新しいデータセットの平均値を計算する。
3. 1と2をB回（例：1,000回〜10,000回）繰り返す：これにより、B個の平均値が得られる。これらは、元のデータから得られる可能性のある平均値の分布（ブートストラップ標本分布）を近似する。
4. 得られた平均値の分布から95%信頼区間を算出する：得られたB個の平均値を小さい順に並べ、下位2.5%と上位2.5%の値をそれぞれ95%信頼区間の下限と上限とする。

---

具体例と R 計算例・グラフ描画

ここでは、架空のテストの点数データを用いて、ブートストラップ法による平均値の95%信頼区間の算出をRで実践してみよう。

データ例： あるクラスの生徒10人のテストの点数

scores <- c(65, 70, 72, 68, 75, 60, 80, 78, 63, 70)

Rでの計算例：

# 必要なパッケージのインストール (まだの場合)
# install.packages("boot")
# install.packages("ggplot2")

# ライブラリの読み込み
library(boot)
library(ggplot2)

# 元のデータ
scores <- c(65, 70, 72, 68, 75, 60, 80, 78, 63, 70)

# データの平均値を計算する関数
mean_function <- function(data, indices) {
  return(mean(data[indices]))
}

# ブートストラップの実行
# R=10000は繰り返し回数（B回）
set.seed(123) # 再現性のためのシード設定
boot_results <- boot(data = scores, statistic = mean_function, R = 10000)

# ブートストラップ結果の表示
print(boot_results)

# 95%信頼区間の計算 (パーセンタイル法)
# type = "perc" はパーセンタイル法を指定
boot_ci <- boot.ci(boot_results, type = "perc")
print(boot_ci)

# ブートストラップ標本分布のヒストグラムと信頼区間の可視化
boot_means <- data.frame(mean = boot_results$t)

ggplot(boot_means, aes(x = mean)) +
  geom_histogram(binwidth = 0.5, fill = "skyblue", color = "black") +
  geom_vline(xintercept = boot_ci$percent[4], color = "red", linetype = "dashed", linewidth = 1) + # 下限
  geom_vline(xintercept = boot_ci$percent[5], color = "red", linetype = "dashed", linewidth = 1) + # 上限
  labs(title = "ブートストラップによる平均値の標本分布と95%信頼区間",
       x = "平均値",
       y = "度数") +
  theme_minimal()
ggsave("Bootstrap_graph_example.png", width = 8, height = 6)

実行結果：

> print(boot_ci)
BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
Based on 10000 bootstrap replicates

CALL : 
boot.ci(boot.out = boot_results, type = "perc")

Intervals : 
Level     Percentile     
95%   (66.4, 73.9 )  
Calculations and Intervals on Original Scale
> 

グラフ描画：

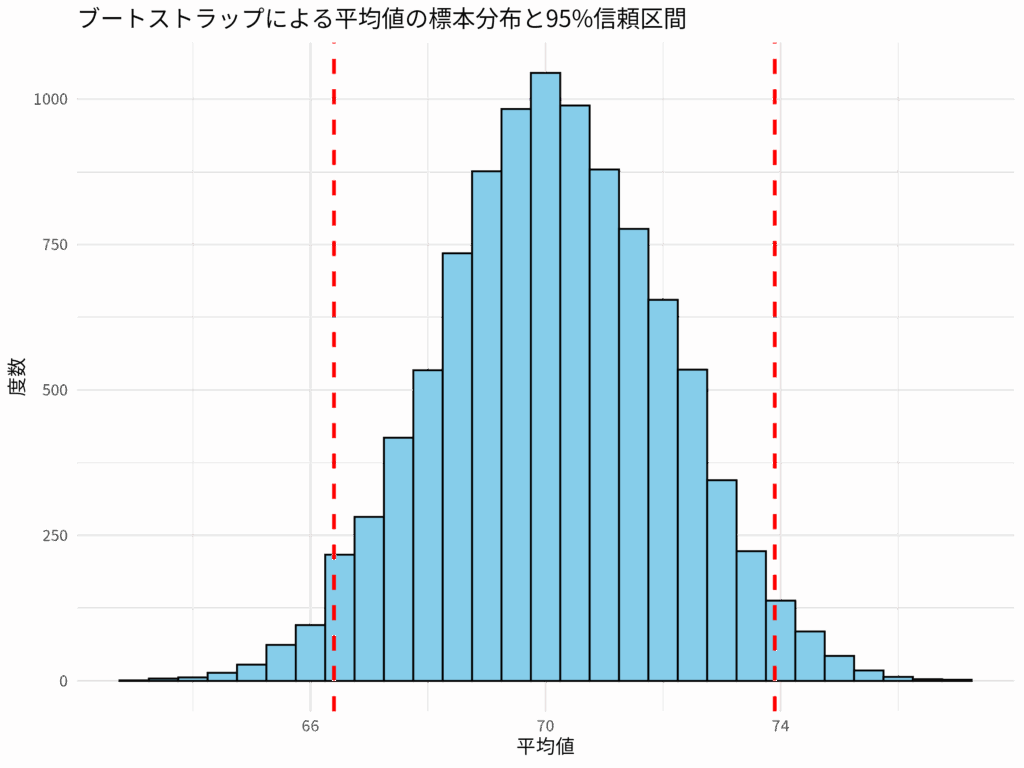
上記のRコードを実行すると、ブートストラップによって得られた平均値の分布を示すヒストグラムと、その中に算出された95%信頼区間の下限と上限を示す垂直線が描画される。このグラフは、平均値がどの範囲に収まる可能性が高いかを視覚的に理解するのに役立つ。

---

結果解釈

上記のRの計算例で得られるboot_ciの結果出力から、ブートストラップ法によって推定された平均値の95%信頼区間は、(66.4, 73.9)であることがわかる。

これは、「もしこの生徒たちと同じような特性を持つ無限の母集団からデータを繰り返し抽出した場合、その平均値の95%は66.4点から73.9点の間に収まるだろう」ということを意味する。言い換えれば、我々は95%の確信をもって、真の平均値がこの区間内にあると考えることができる。

ブートストラップ法は、特定の分布を仮定しないため、データが正規分布に従わない場合や、標本サイズが小さい場合でも適用できるという大きなメリットがある。

---

まとめ

ブートストラップ法は、限られたデータからでも信頼性の高い推定を行うための強力なツールである。特に、平均値の信頼区間を推定する際に、従来のパラメトリックな手法が適用しにくい状況でその真価を発揮する。

今回の記事で紹介したRでの具体的な計算例とグラフ描画を通じて、ブートストラップ法の概念と実践的な使い方を理解していただけただろうか。ぜひ、手元のデータ解析にブートストラップ法を応用してみてほしい。より堅牢で信頼性の高い統計的推論が可能になるはずである。