回帰分析を行う際、2つ以上の説明変数が従属変数に与える影響が、互いの水準によって異なる場合がある。このような現象を「交互作用(interaction)」と呼び、統計モデルに交互作用項を組み込むことで、より詳細な関係性を明らかにできる。
しかし、交互作用が有意であった場合に、どのようにその結果を記述し、さらに深掘りした解析(サブグループ解析)をどのように論文に落とし込むべきか、悩む研究者は少なくないだろう。
本記事では、重回帰分析において連続データの説明変数とカテゴリカルデータの交互作用項が有意であった場合の記述方法、特にその後のサブグループ解析の論文での記述方法について、Rの具体例を交えながら解説する。
交互作用とは何か?
交互作用とは、ある説明変数と別の説明変数が、目的変数に対して独立に影響するのではなく、互いに影響し合いながら目的変数に影響を与える現象を指す。
例えば、「学習時間」と「性別」が「試験の点数」に影響を与える場合を考えてみよう。もし男性の方が学習時間が増えるほど点数が伸びやすいが、女性では学習時間が増えても点数はあまり伸びない、という傾向があれば、これは学習時間と性別の間に交互作用があると言える。
回帰モデルに交互作用項を含める方法
Rでは、回帰モデルに交互作用項を含めるのは非常に簡単である。* 演算子を使用するか、: 演算子を使用して個別に交互作用項を指定する。
例:
目的変数 Y、連続説明変数 X、カテゴリカル説明変数 Group(2つの水準AとBを持つとする)がある場合
*演算子を用いる方法(主効果と交互作用の両方を含む):Rmodel <- lm(Y ~ X * Group, data = mydata)これはY ~ X + Group + X:Groupと同等である。:演算子を用いる方法(交互作用のみを含む):Rmodel <- lm(Y ~ X + Group + X:Group, data = mydata)
多くの場合、* 演算子を用いる方法が簡潔で分かりやすいだろう。
論文での記述方法:交互作用が有意な場合
交互作用項を含む回帰モデルを分析し、その結果、交互作用が統計的に有意であった場合、以下の点を明確に記述することが重要である。
モデルの提示と交互作用の確認
まず、構築した回帰モデルと、交互作用項の有意性を示す統計量を提示する。
記述例:
目的変数であるYに対する連続変数Xとカテゴリカル変数Groupの影響を検討するため、重回帰分析を実施した。分析の結果、モデル全体は統計的に有意であり ($F(\text{df1, df2}) = 〜, p < .001$)、決定係数 R2 は 〜 であった。特に、連続変数Xとカテゴリカル変数Groupの間の交互作用は統計的に有意であった(p=〜)。
ここで、Groupがダミー変数としてどのようにコーディングされているか(例:Group Aを基準とした場合など)も明記すると良い。
交互作用の解釈
交互作用が有意であるということは、一方の変数の影響がもう一方の変数の水準によって異なることを意味する。この「異なる」という点を具体的に記述する。
記述例:
この有意な交互作用は、連続変数Xが目的変数Yに与える影響が、カテゴリカル変数Groupの水準によって異なることを示唆している。具体的には、GroupがAのグループではXの効果が〇〇であったのに対し、GroupがBのグループではXの効果が△△であった。
この解釈を裏付けるために、後述するサブグループ解析が非常に重要となる。
有意な交互作用後のサブグループ解析と記述方法
交互作用が有意であった場合、それぞれのサブグループ(カテゴリカル変数の各水準)において、連続変数が目的変数にどのような影響を与えるのかを詳細に分析する「サブグループ解析」を行うのが一般的である。
サブグループ解析の実施
サブグループ解析は、カテゴリカル変数の各水準ごとにデータを分割し、それぞれのサブグループ内で回帰分析を行うことで実施する。
Rでの具体例:
# 仮想データの作成
set.seed(123)
mydata <- data.frame(
Y = rnorm(100, 50, 10),
X = rnorm(100, 10, 2),
Group = sample(c("A", "B"), 100, replace = TRUE)
)
# 交互作用項を含むモデル
model_interaction <- lm(Y ~ X * Group, data = mydata)
summary(model_interaction)
# ここで、X:Group のp値が有意であったと仮定する(実際は以下の結果のとおり有意ではなかった)
# サブグループAの解析
data_groupA <- subset(mydata, Group == "A")
model_groupA <- lm(Y ~ X, data = data_groupA)
summary(model_groupA)
# サブグループBの解析
data_groupB <- subset(mydata, Group == "B")
model_groupB <- lm(Y ~ X, data = data_groupB)
summary(model_groupB)
実行結果:
> # 交互作用項を含むモデル
> model_interaction <- lm(Y ~ X * Group, data = mydata)
> summary(model_interaction)
Call:
lm(formula = Y ~ X * Group, data = mydata)
Residuals:
Min 1Q Median 3Q Max
-22.3817 -6.1564 -0.4205 5.3336 21.1901
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 48.94371 6.99528 6.997 3.52e-10 ***
X 0.03418 0.71035 0.048 0.962
GroupB 8.84534 9.47952 0.933 0.353
X:GroupB -0.56560 0.95193 -0.594 0.554
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 9.086 on 96 degrees of freedom
Multiple R-squared: 0.03925, Adjusted R-squared: 0.009224
F-statistic: 1.307 on 3 and 96 DF, p-value: 0.2766
> # サブグループAの解析
> data_groupA <- subset(mydata, Group == "A")
> model_groupA <- lm(Y ~ X, data = data_groupA)
> summary(model_groupA)
Call:
lm(formula = Y ~ X, data = data_groupA)
Residuals:
Min 1Q Median 3Q Max
-22.382 -6.239 -1.437 6.908 21.190
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 48.94371 7.84947 6.235 1.09e-07 ***
X 0.03418 0.79709 0.043 0.966
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 10.2 on 48 degrees of freedom
Multiple R-squared: 3.832e-05, Adjusted R-squared: -0.02079
F-statistic: 0.001839 on 1 and 48 DF, p-value: 0.966
> # サブグループBの解析
> data_groupB <- subset(mydata, Group == "B")
> model_groupB <- lm(Y ~ X, data = data_groupB)
> summary(model_groupB)
Call:
lm(formula = Y ~ X, data = data_groupB)
Residuals:
Min 1Q Median 3Q Max
-17.3641 -4.9425 0.7553 3.4312 20.0368
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 57.7890 5.5065 10.495 5.09e-14 ***
X -0.5314 0.5454 -0.974 0.335
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 7.821 on 48 degrees of freedom
Multiple R-squared: 0.01939, Adjusted R-squared: -0.001038
F-statistic: 0.9492 on 1 and 48 DF, p-value: 0.3348
>
論文での記述方法:サブグループ解析の結果
サブグループ解析の結果は、それぞれのグループにおける連続変数の効果を明確に比較できるように記述する。
記述例:
連続変数Xとカテゴリカル変数Groupの有意な交互作用が確認されたため、さらにGroupの各水準におけるXのYに対する影響を調べるため、サブグループ解析を実施した。
「Group Aにおける解析」
GroupがAのサブグループにおいて、連続変数Xは目的変数Yに対して統計的に有意な正の影響を示した(回帰係数 = Estimate of GroupA, SE=SE of GroupA, t=t−value of GroupA, p=p−value of GroupA)。具体的には、Xが1単位増加するごとに、Yは Estimate of GroupA 単位増加すると推定された。(表で提示しない場合、上記のように詳細に書くのがよい)
「Group Bにおける解析」
一方、GroupがBのサブグループでは、連続変数Xは目的変数Yに対して統計的に有意な影響を示さなかった(あるいは、有意な負の影響を示した、など具体的に記述する)(回帰係数 = Estimate of GroupB, SE=SE of GroupB, t=t−value of GroupB, p=p−value of GroupB)。この結果は、GroupがAのグループと比較して、XのYへの影響が質的に(または量的に)異なることを明確に示している。(表で提示しない場合、上記のように詳細に書くのがよい)
結果の要約と考察
最後に、交互作用とサブグループ解析の結果を要約し、その学術的な意義や臨床的な意味について考察する。
記述例:
以上の結果から、連続変数Xが目的変数Yに与える影響は、カテゴリカル変数Groupの水準によって大きく異なることが明らかになった。特に、Group AにおいてはXの正の効果が認められたのに対し、Group Bではその効果が認められない(または効果の方向が異なる)ことが示された。この知見は、今後〇〇な介入を行う際に、Groupの特性を考慮する必要があることを示唆している。今後の研究では、なぜこのような交互作用が生じるのか、そのメカニズムについてさらに詳細な検討が必要である。
図を用いた可視化
交互作用の結果は、図を用いることでより直感的に理解しやすくなる。カテゴリカル変数ごとの散布図に回帰直線を描画したり、予測値プロットを作成したりすると良い。
Rでの例(ggplot2を使用):
library(ggplot2)
ggplot(mydata, aes(x = X, y = Y, color = Group)) +
geom_point(alpha = 0.6) +
geom_smooth(method = "lm", se = TRUE) + # サブグループごとに回帰直線を描画
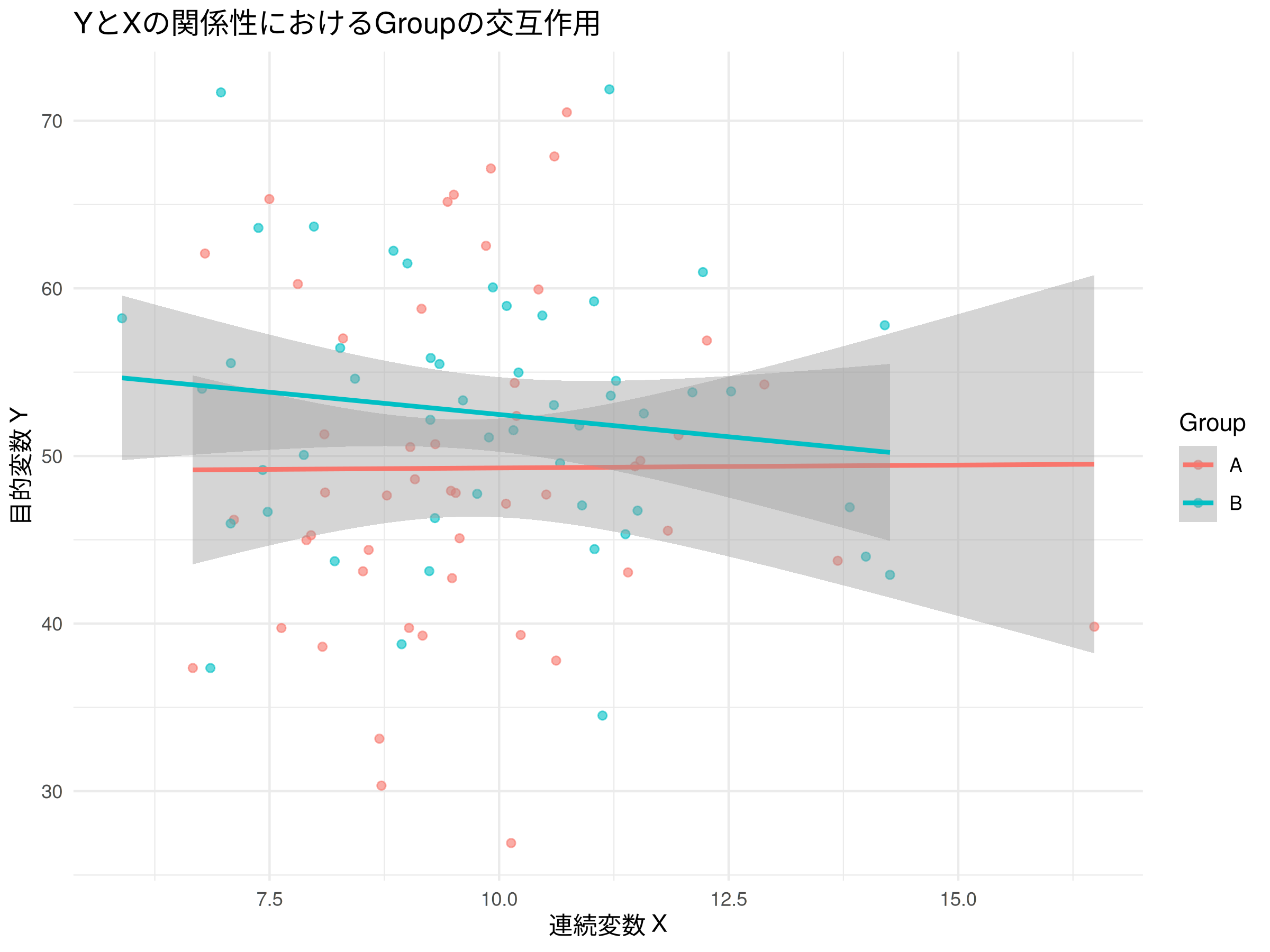
labs(title = "YとXの関係性におけるGroupの交互作用",
x = "連続変数 X",
y = "目的変数 Y") +
theme_minimal()
ggsave("linear_regression_interaction_term.png", width = 8, height = 6)
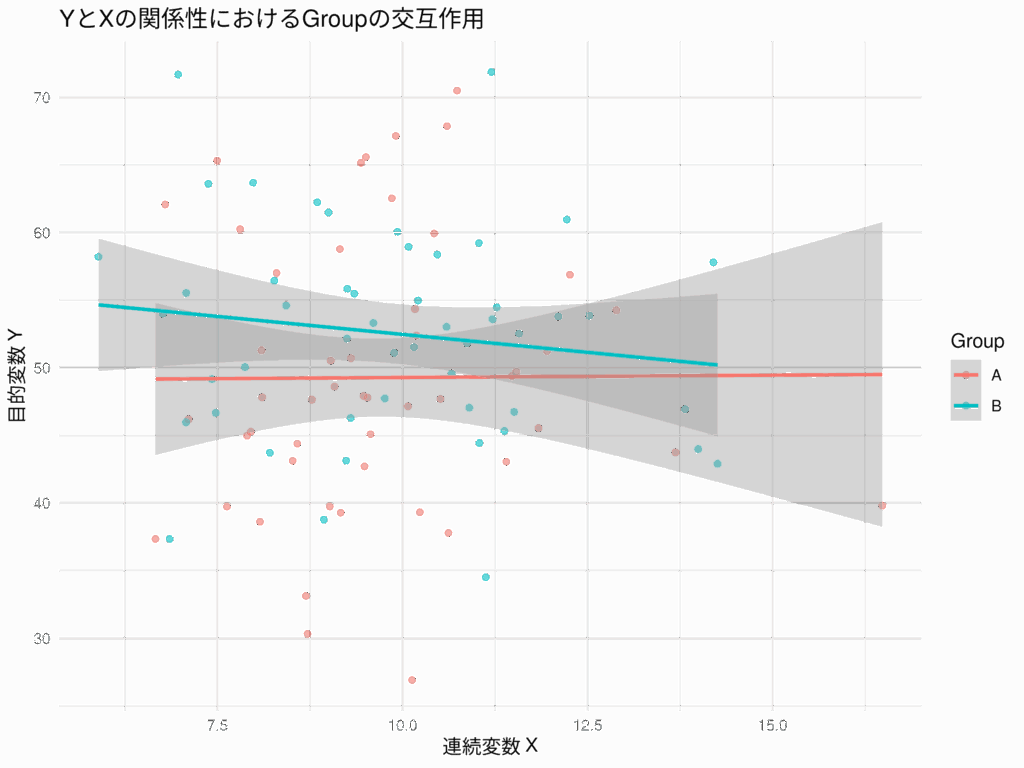
図で見ても、傾きが Group ごとに異なると言い切ることはできず、交互作用があるとは言えないという解析結果を裏付ける結果となった。
まとめ
交互作用項を含む回帰分析は、データ間の複雑な関係性を明らかにする強力なツールである。特に交互作用が有意であった場合、単にその有意性を報告するだけでなく、サブグループ解析を通じてその具体的な意味を深く掘り下げ、分かりやすく記述することが重要である。本記事で紹介した記述方法とRの具体例が、あなたの研究論文作成の一助となれば幸いである。





コメント