新しい検査機器を導入する際、最も重要なプロセスは「その機器がどれだけ正確か」を客観的に証明することである。しかし、ここで多くの人が陥る罠がある。それは「相関関係(R²)さえ高ければ、機器の性能は十分である」と思い込んでしまうことだ。
本記事では、妥当性評価の基本であるR²(決定係数)と、臨床・研究現場で不可欠なBland-Altman(ブランド・アルトマン)プロットについて、それぞれの役割と使い分けを初心者向けに解説する。
検査機器の妥当性評価が必要な理由
新しい検査機器や測定法を導入する際は、すでに信頼が確立されている「基準法(ゴールドスタンダード)」と比較し、以下の2点を確認しなければならない。
- 正確性: 基準となる値とどれだけ近いか。
- 信頼性: 測定を繰り返しても、常に安定した結果が得られるか。
これらを評価するためには、単に数値が似ているかどうかを見る「相関」だけでなく、数値がどれだけ一致しているかという「一致度」の視点が不可欠である。
R²(決定係数):データの「連動性」を評価する
統計学において、2つの変数の関係性を表す際によく用いられるのが「R²(決定係数)」である。
R²の定義と意味
R²は、2つの測定値がどれくらい「連動して動いているか」を0から1の範囲で示す指標である。
- 1に近い: 2つのデータの動きが非常に似ている(強い正の相関)。
- 0に近い: 2つのデータに関連性は認められない。
R²の限界:相関が高いことは「一致」を意味しない
ここが妥当性評価における最大の注意点である。「相関が強くても、数値が一致しているとは限らない」のである。
例えば、新しい機器が基準法よりも常に「+10」高い値を出しているケースを想定する。この場合、グラフ上ではきれいな直線(高いR²)を描くが、検査値としては常に10の誤差が生じている。このように、一定の方向にズレが生じる「系統的誤差」をR²だけで検出することは不可能である。
Bland-Altman Plot:数値の「一致度」を可視化する
R²の弱点を補い、測定値間の具体的な「誤差」を視覚的に明らかにする手法が「Bland-Altmanプロット」である。
Bland-Altman Plotの定義
2つの測定方法の「一致度」を評価するための散布図である。単なる連動性ではなく、「具体的に何単位くらいの誤差が生じているか」を浮き彫りにする。
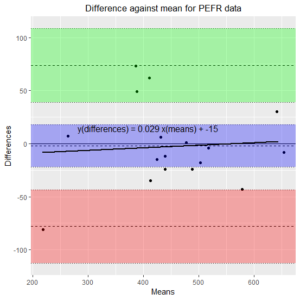
グラフの構成要素
- 横軸: 2つの測定値の平均(真の値に近いと想定される値)。
- 縦軸: 2つの測定値の差(「新しい機器」マイナス「基準法」)。
- 一致の限界(Limits of Agreement, LoA): 差の平均値から±1.96倍の標準偏差の範囲。データの約95%がこの範囲に収まることを示し、許容できる誤差かどうかを判断する基準となる。
Bland-Altman Plotの利点
- 系統的誤差の検出: 常に一定のズレがあるのか、あるいは測定値が大きくなるほど誤差も拡大するのかといった傾向が一目で判別できる。
- 臨床的判断の支援: 「LoAの範囲(誤差の幅)が、実際の診断や治療において許容できるかどうか」を具体的に検討できる。
評価方法の適切な使い分け
妥当性の評価においては、どちらか一方を用いるのではなく、両方の指標を併用することが推奨される。
| 評価方法 | 適した場面 | 明らかにできること |
| R² (決定係数) | 予備的な性能確認 | 2つの数値に「関係性」があるか |
| Bland-Altman | 実践的な精度評価 | 臨床で許容できる「誤差」か |
理想的な評価のアプローチ
- まずはR²を算出し、2つの機器の測定値に関連があることを確認する。
- 次にBland-Altmanプロットを作成し、具体的な誤差の量や傾向を詳細に分析する。
まとめ:総合的な視点による妥当性評価
検査機器の妥当性を評価する際、R²による「相関」の確認だけでは不十分である。Bland-Altmanプロットを併用し、多角的に分析することで初めて、その機器が現場で信頼に足るものかどうかが判断可能となる。
「相関は高いが、実は見逃せない誤差が隠れていた」という事態を防ぐためにも、これら2つのツールを適切に組み合わせた総合的なアプローチが必要である。
おすすめ書籍
誰も教えてくれなかった 医療統計の使い分け〜迷いやすい解析手法の選び方が,Rで実感しながらわかる!





コメント