医療統計やデータ分析において、予測モデルの精度を評価する際に「ROC曲線」は欠かせない指標である。しかし、生存時間解析のように「時間の経過」が関わるデータでは、通常のROC曲線だけでは不十分な場合が多い。
そこで用いられるのが「時間依存性ROC曲線(Time-dependent ROC curve)」である。本記事では、その概念からRを用いた具体的な実装方法までを解説する。
時間依存性ROC曲線とは
通常のROC曲線は、「病気の有無」など、ある一時点の固定された状態を判定する。
しかし、生存分析においては、時間の経過とともに予測の難易度やモデルの精度が変化する。
- 「手術直後の急変は予測できるが、数年後の再発予測は難しい」
- 「特定の検査値は、短期的な予後予測には強いが、長期予測には向かない」
このように、「時点 $t$ における予測精度」を評価できるのが、時間依存性ROC曲線の特徴である。特定のタイミングにおけるモデルの「実力」を可視化するツールと言い換えることができる。
時間依存性ROC曲線の使い所
主に以下のようなシチュエーションで活用される。
- 予後予測モデルの評価: 作成したスコアが、特定の時期(例:2年目)にどれほど正確に機能しているかを判定する。
- バイオマーカーの比較: 複数の指標のうち、どの変数が特定の時点において最も高い予測能を持つかを比較検討する。
- 臨床的妥当性の確認: 「治療後〇年時点でのリスクを精度高く予測したい」という、臨床現場の具体的なニーズに合致しているかを評価する。
Rによる時間依存性ROC曲線の描画
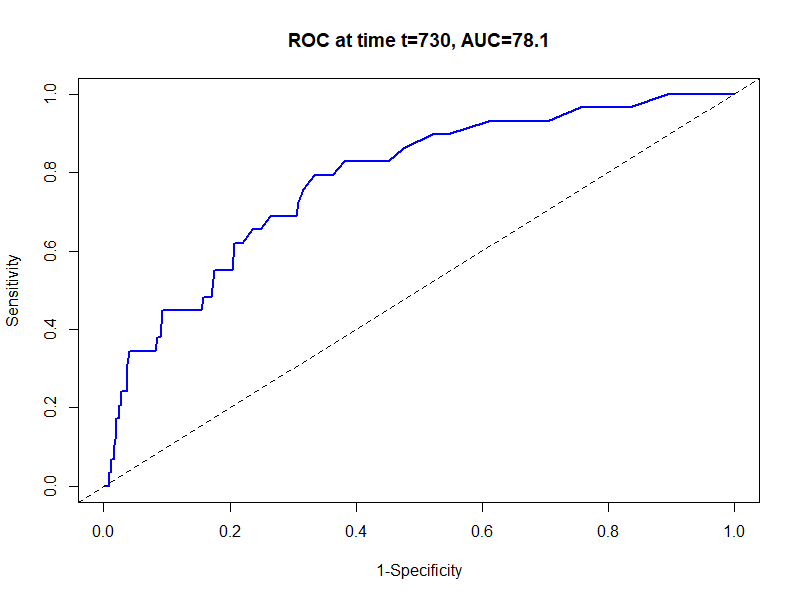
Rの timeROC パッケージを使用すれば、簡潔なコードで計算と可視化が可能である。ここでは、生存時間解析で汎用される pbc データ(原発性胆汁性胆管炎データ)を用い、ビリルビン値による「2年(730日)時点」の予測精度を評価する。
ステップ1:パッケージの準備とデータ整形
まずは必要なライブラリを読み込み、データを整える。
# パッケージのインストールと読み込み
install.packages("timeROC") # 最初の一回のみ
library(timeROC)
library(survival)
# サンプルデータ(pbc)の読み込み
data(pbc)
pbc <- na.omit(pbc) # 欠損値を除外
pbc$event <- ifelse(pbc$status == 2, 1, 0) # 死亡を1、それ以外を0に変換
ステップ2:計算と可視化
2年(730日)時点でのROC曲線を計算し、描画する。
# 時間依存性ROCの計算(2年=730日時点)
res <- timeROC(T = pbc$time, # 生存時間
delta = pbc$event, # イベントフラグ
marker = pbc$bili, # 予測変数(ビリルビン値)
cause = 1, # イベント(死亡)のコード
weighting = "marginal", # 重み付けの方法
times = 730) # 評価したい時点(日単位)
# グラフの描画
# plot関数により、タイトルに自動でその時点のAUCが出力される(単位は%)
plot(res, time = 730, col = "blue", lwd = 2)
解説:weighting = “marginal” の意味合い
timeROC 関数の引数に指定した weighting = "marginal" は、生存時間データ特有の「打ち切り(追跡不能)」を統計的に調整するための設定である。
- 手法の背景: 生存時間データには、イベントが発生する前に観察が終了するケースが含まれる。この偏りを調整するために、「逆確率打ち切り重み付け(IPCW)」という手法が用いられる。
- marginal(周辺)の意味: これは最も標準的な設定であり、「打ち切りの発生しやすさが、予測因子(今回はビリルビン値)には依存せず、時間のみに依存する」と仮定して計算を行うことを意味する。
解析の第一歩としては、この marginal 設定を選択するのが一般的かつ妥当である。
【コラム】IPCWとは?:IPTWとの違い
統計学に詳しい方なら、因果推論で使われる「IPTW(逆確率治療重み付け)」を聞いたことがあるかもしれない。時間依存性ROC曲線で使われるIPCWは、その「打ち切り(Censoring)」版である。
- IPTW: 治療(Treatment)を受ける確率の逆数で重み付けし、集団間の背景因子を揃える。
- IPCW: 打ち切り(Censoring)が発生する確率の逆数で重み付けし、打ち切りによるデータの偏りを補正する。
生存時間解析では、時間の経過とともに「追跡不能(打ち切り)」になる症例が増えていく。もし「重症な人ほど打ち切られやすい」といった偏りがある場合、残ったデータだけで計算したAUCは、実際の精度よりも高く(あるいは低く)見積もられてしまう。
IPCWを用いることで、「もし打ち切りが発生しなかったら、そのデータはどうなっていたか」を擬似的に再現し、より現実に即した予測精度を算出することが可能になるのである。
まとめ
時間依存性ROC曲線は、生存分析における予測精度の「通知表」であり、モデルの有効期間を把握するために不可欠な手法である。
- 時点の特定: 「特定のタイミング」での予測力を明確にできる。
- 自動評価: Rの
plot()関数を用いることで、容易にAUCを確認できる。 - 打ち切りの考慮:
marginal設定により、生存分析特有のデータの偏りを補正できる。
自身の研究や解析においても、通常のROC曲線で終始せず、時間依存性ROC曲線を用いて多角的に精度を評価することを推奨する。
おすすめ書籍
誰も教えてくれなかった 医療統計の使い分け〜迷いやすい解析手法の選び方が,Rで実感しながらわかる!






コメント