その「オッズ比」で大丈夫か？リスク比を正しく推定する「修正ポアソン回帰」のすゝめ

---

「分析の結果、リスクが3倍になった」

こうした報告を耳にした際、注意が必要なケースがある。もしロジスティック回帰を用いてその数字を導き出したのであれば、実はリスクを過大評価している可能性があるからだ。

本記事では、医学論文やマーケティング分析において重要視される手法、修正ポアソン回帰（Modified Poisson Regression）について、その必要性と実装方法を解説する。

---

「オッズ比」と「リスク比」の混同という落とし穴

「0か1か（イベントの発生有無）」を扱うデータ分析において、最も一般的な手法はロジスティック回帰である。しかし、ロジスティック回帰で得られる指標は「オッズ比（Odds Ratio）」であり、私たちが直感的に理解したい「リスク比（Relative Risk）」とは性質が異なる。

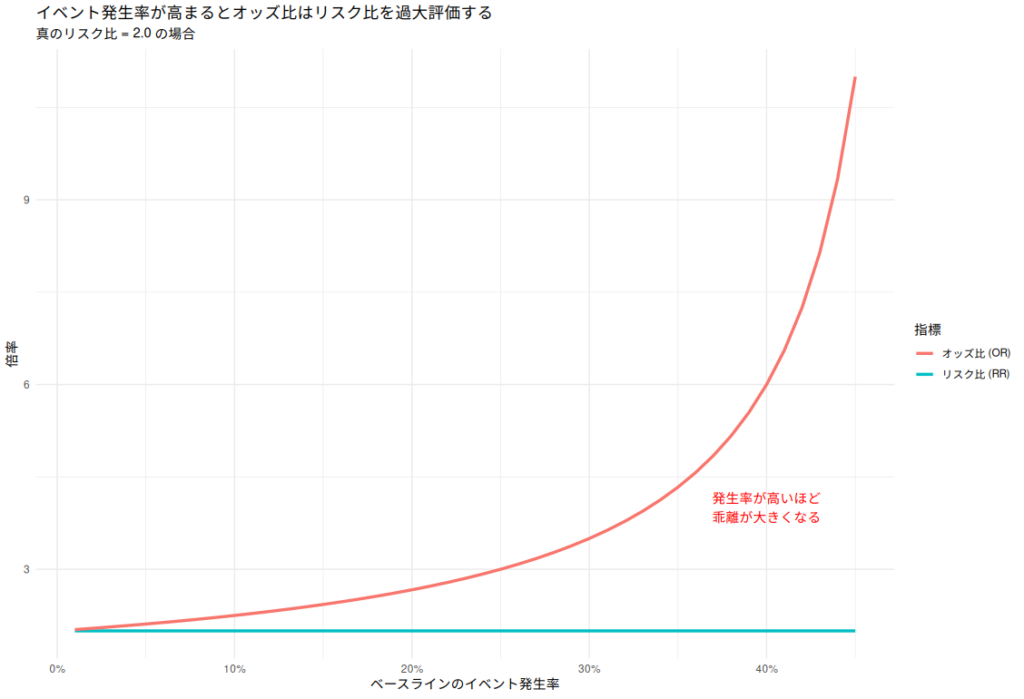
• イベント発生率が低い場合（目安5%以下）: オッズ比とリスク比は近似する。
• イベント発生率が高い場合: オッズ比はリスク比よりも大きな値（過大評価）を示す性質がある。

イベントが頻繁に発生するデータにおいて、「リスクが2倍」と伝えるべき場面で、オッズ比を用いると「4倍」といった誇張された結果を招くリスクがあるのだ。

---

リスク比を求める手法の比較

リスク比を直接推定したい場合、候補となる3つの手法の特性は以下の通りである。

手法	推定指標	計算の安定性	特徴
ロジスティック回帰	オッズ比	◎ 非常に安定	定番だが、発生率が高いとリスク比から乖離する。
対数二項回帰	リスク比	△ 不安定	理論的に自然だが、収束不全（エラー）が起きやすい。
修正ポアソン回帰	リスク比	○ 安定	計算が安定しており、かつリスク比を正しく出せる。

実務において、計算の安定性と解釈の容易さを両立できるのが、修正ポアソン回帰の最大の強みである。

---

なぜ「修正」が必要なのか（分散の過大評価）

本来、ポアソン回帰はカウントデータ（件数）を扱うためのモデルである。これを二値データに適用すると、モデル内では以下のような「誤解」が生じる。

ポアソン分布の性質上、モデルは「分散は平均に等しい」と仮定する。しかし、二値データ（ベルヌーイ分布）の実際の分散は、数学的にポアソン分布の想定よりも必ず小さくなる。

そのため、通常のポアソン回帰をそのまま適用すると、モデルは「データが想定以上にバラついている」と判断し、標準誤差（信頼区間）を不当に大きく見積もってしまう。この誤解を解き、標準誤差を適切な値に補正するために「修正」が必要となるのである。

---

サンドイッチ推定法は「仕立て直しのピン留め」

この修正に用いられる技術が「サンドイッチ推定法（ロバスト標準誤差）」である。これは、いわば「既製品のスーツを、実際の体型に合わせてピン留めで補正する」ような作業だ。

• パン（モデルの仮定）: ポアソン回帰という既製品の型紙。
• 具（実際のデータ）: 目の前にある現実のバラツキ。
• サンドイッチ: 型紙（パン）で現実のデータ（具）を挟み込むことで、データの実態に即した正確な標準誤差を算出する。

この補正を行うことで、モデルの「勘違い」が正され、信頼区間は適切に引き締まる。

---

Rによる実装

R言語では、標準的な glm 関数とパッケージを組み合わせることで容易に実装が可能である。

# 必要なライブラリ
if (!require("sandwich")) install.packages("sandwich")
if (!require("lmtest")) install.packages("lmtest")
library(sandwich)
library(lmtest)

# 0. サンプルデータの作成
set.seed(123)
n <- 500
# 曝露あり(1)・なし(0)を半分ずつ
exposure <- rbinom(n, 1, 0.5)
# 年齢（共変量）
age <- rnorm(n, 50, 10)

# リスク（確率）を計算：曝露があるとリスクが2倍になる設定
# (ベースライン25% → 曝露ありで50%程度になるように調整)
p <- 0.25 * exp(log(2) * exposure + 0.01 * (age - 50))
p <- pmin(p, 0.9) # 確率は1を超えないように
outcome <- rbinom(n, 1, p)

df <- data.frame(outcome, exposure, age)

# 1. モデルの構築（family = poisson(link = "log") を指定）
model <- glm(outcome ~ exposure + age, data = df, family = poisson(link = "log"))
summary(model)$coef

# 2. ロバスト標準誤差による修正（サンドイッチ推定）
# type = "HC0" が修正ポアソン回帰における標準的な指定
res <- coeftest(model, vcov = vcovHC(model, type = "HC0"))
print(res) # SEが小さくなっているのがわかる

# 3. 指数関数にかけてリスク比（RR）と信頼区間を算出
RR_results <- exp(cbind(RR = coef(model), confint.default(model, vcov = vcovHC(model, type = "HC0"))))
print("--- 修正ポアソン回帰の結果 (リスク比) ---")
print(RR_results)

---

出力結果

> # 1. モデルの構築（family = poisson(link = "log") を指定）
> summary(model)$coef
               Estimate  Std. Error   z value     Pr(>|z|)
(Intercept) -2.18856558 0.406003661 -5.390507 7.025917e-08
exposure     0.77196171 0.156385251  4.936282 7.962592e-07
age          0.01460124 0.007536578  1.937384 5.269848e-02


> # 2. ロバスト標準誤差による修正（サンドイッチ推定）
> print(res) # SEが小さくなっているのがわかる

z test of coefficients:

              Estimate Std. Error z value  Pr(>|z|)    
(Intercept) -2.1885656  0.3074785 -7.1178 1.097e-12 ***
exposure     0.7719617  0.1277737  6.0416 1.526e-09 ***
age          0.0146012  0.0056927  2.5649   0.01032 *  
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1


> # 3. 指数関数にかけてリスク比（RR）と信頼区間を算出
> print("--- 修正ポアソン回帰の結果 (リスク比) ---")
[1] "--- 修正ポアソン回帰の結果 (リスク比) ---"
> print(RR_results)
                   RR      2.5 %    97.5 %
(Intercept) 0.1120774 0.05057398 0.2483756
exposure    2.1640072 1.59273434 2.9401811
age         1.0147084 0.99982984 1.0298083

ロバスト標準誤差で修正を行うと、広すぎると勘違いしていた分散が修正されて、小さくなっているのがわかる。

まとめ：誠実な解析が信頼を生む

オッズ比は強力な指標であるが、万能ではない。特にイベント発生率が10%を超えるようなケースでは、オッズ比をリスク比のように解釈することは危険を伴う。

「リスクが何倍になったか」を直感的かつ正確に報告したいのであれば、修正ポアソン回帰は極めて有効な選択肢となる。計算の安定性と誠実な推定。この二つを兼ね備えた手法を使いこなすことは、分析者としての信頼性を高める一助となるだろう。

おすすめ書籍

誰も教えてくれなかった　医療統計の使い分け〜迷いやすい解析手法の選び方が，Rで実感しながらわかる！

---