エラスティックネットを簡単に解説
R で実行する方法も解説
リッジ・ラッソ・エラスティックネットとは?
線形回帰モデルは、係数 β(パラメータ)を推定するときに最小二乗法を用いる。
通常の最小二乗法は、従属変数の実測値とモデルから計算された値との差=残差を二乗して足し合わせる。
この合計が最小になるパラメータのセットを見つける。
リッジ、ラッソ(LASSO)、エラスティックネットは残差の二乗和に以下の式を足したものを最小にする方法を取る。「罰則」と呼ぶ。
$$ \lambda \left( \frac{1 – \alpha}{2} || \beta ||_2^2 + \alpha || \beta ||_1 \right) $$
$$ = \lambda \sum_{j=1}^p \left( \frac{1 – \alpha}{2} \beta_j^2 + \alpha |\beta_j| \right) $$
リッジは最初の項だけ、ラッソは後の項だけ、エラスティックネットはどちらの項も使う方法だ。
α が0の時はリッジ、α が1の時はラッソ、0と1の間のときはエラスティックネットになる。
最初の項は$ \beta^2 $ の和になっている。
後の項は β の絶対値の和になっている。
いずれも β が多くなる、大きくなると、全体が大きくなる。
つまり、どんなに残差二乗和が小さくなるようにしても、この項たちが大きくなったのでは、目的が達成できない。
「罰則」と呼ばれるゆえんだ。
β を小さくする、いくつかを0にするなどして、「罰則」を小さくする。
結果として、当てはまりすぎ(過学習)を防ぐことになる。
ちなみに $ || \beta ||_2^2 $ とか、$ || \beta ||_1 $ はノルムと呼ばれる。
$$ || \beta ||_2^2 = \sqrt{| \beta |_1^2 + |\beta|_2^2 + \cdots + |\beta|_n^2} $$
$$ ||\beta||_1 = |\beta|_1 + |\beta|_2 + \cdots + |\beta|_n $$
リッジ・ラッソ・エラスティックネットの名前の由来
リッジ(Ridge)は、一般的な意味は盛り上がった場所、例えば山の背、尾根など。
二乗和の項を入れることで、上に凸型の二次反応関数に、数学的類似性があるところから名づけられた。
ラッソ(LASSO)は、Least Absolute Shrinkage and Selection Operator の頭文字語。
係数の絶対値(Absolute)を用いる方法で、係数を小さくして(Shrinkage)罰則を小さくし、要らない変数の係数をゼロにして変数を選択する(Selection)方法だ。
エラスティックネット(Elastic net)は、まるで伸縮性の投網のように「大きな魚(重要な係数)全部」を残すイメージからつけられた名前だ。
エラスティックネットを R で実行するために必要なパッケージの準備
最初に一回インストール。
glmnetパッケージとISLRパッケージ。
install.packages("glmnet")
install.packages("ISLR")
ともに呼び出しておく。
library(glmnet)
library(ISLR)
エラスティックネットを R で行ってみる例題のデータを準備
ISLRパッケージ中のCollegeデータを使う。
米国の777大学の出願者や学生数、書籍購入にかかるコストなどという18個のプロファイルデータ。
学習データとテストデータに分ける。
5分の4を学習データ。5分の1をテストデータにする。
set.seed(20180921)
sub <- sample(1:777, round(777*4/5))
例題は、登録する学生数(Enroll)を予測するモデルを作ること。
エラスティックネットの前に従来の最小二乗法を実行してみる
Enrollをその他の変数全部で予測する回帰式を作る。
lm.res <- lm(Enroll ~ ., data=College[sub,])
summary(lm.res)
以下のように計算結果が表示される。
> summary(lm.res)
Call:
lm(formula = Enroll ~ ., data = College[sub, ])
Residuals:
Min 1Q Median 3Q Max
-1577.18 -63.47 -12.88 45.64 1581.09
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 219.946039 87.176801 2.523 0.011892 *
PrivateYes -20.716365 29.254284 -0.708 0.479126
Apps -0.040325 0.007908 -5.099 4.57e-07 ***
Accept 0.162698 0.014738 11.040 < 2e-16 ***
Top10perc 4.381100 1.270779 3.448 0.000605 ***
Top25perc -2.206551 0.943228 -2.339 0.019642 *
F.Undergrad 0.142490 0.004467 31.901 < 2e-16 ***
P.Undergrad -0.029804 0.008131 -3.666 0.000269 ***
Outstate -0.004381 0.004120 -1.063 0.288023
Room.Board -0.018011 0.010351 -1.740 0.082361 .
Books 0.018743 0.049424 0.379 0.704654
Personal -0.004377 0.014736 -0.297 0.766533
PhD 0.353353 1.024941 0.345 0.730399
Terminal -1.275895 1.139472 -1.120 0.263276
S.F.Ratio -0.842953 2.686361 -0.314 0.753789
perc.alumni 1.920409 0.879343 2.184 0.029353 *
Expend 0.001368 0.002644 0.517 0.605075
Grad.Rate 0.277165 0.639241 0.434 0.664745
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 199.2 on 604 degrees of freedom
Multiple R-squared: 0.9529, Adjusted R-squared: 0.9516
F-statistic: 718.9 on 17 and 604 DF, p-value: < 2.2e-16
モデルから得られる予測値と実測値のかい離を mean squared error of prediction (MSEP) で確認する。
mean((predict(lm.res)-College[sub,]$Enroll)^2)
> mean((predict(lm.res)-College[sub,]$Enroll)^2)
[1] 38530.83
学習データから得られたモデルをテストデータに適用して、テストデータで得られる予測値と実測値のかい離を MSEP で確認する。
lm.test <- predict(lm.res, newdata=College[-sub,])
mean((lm.test - College[-sub,]$Enroll)^2)
> mean((lm.test - College[-sub,]$Enroll)^2)
[1] 47213.26
MSEPはテストデータで大きくなった。
これは学習データでの予測モデルの性能があまり高くないことを示している。
リッジで解析した結果
glmnetパッケージのglmnet()を使う。
データは行列で与える。
data.matrix()を使う。
説明変数, 従属変数の順番に指定し、alpha=0を指定する。
ridge.res <- glmnet(data.matrix(College[sub,-4]), College[sub,]$Enroll, alpha=0)
mean((predict(ridge.res, newx=data.matrix(College[sub, -4]))-College[sub,]$Enroll)^2)
ridge.test <- predict(ridge.res, newx=data.matrix(College[-sub,-4]))
mean((ridge.test - College[-sub,]$Enroll)^2)
学習データで作られたモデルを、学習データとテストデータの MSEP で見てみると、テストデータでははるかに MSEP が大きくなっている。
あまり予測性能はよくない。
> mean((predict(ridge.res, newx=data.matrix(College[sub, -4]))-College[sub,]$Enroll)^2)
[1] 442744.8
> mean((ridge.test - College[-sub,]$Enroll)^2)
[1] 558366.1
予測性能を上げる方法として、クロスバリデーション(cross-validation)という方法がある。
学習データをさらに分割して、テストセット1つと学習セットとして繰り返し、最適な λ を見つける方法。
学習データにcross-validation付きのglmnetを適用して、結果をプロットする。
ridge.res.cv <- cv.glmnet(data.matrix(College[sub,-4]), College[sub,]$Enroll, alpha=0)
plot(ridge.res.cv)
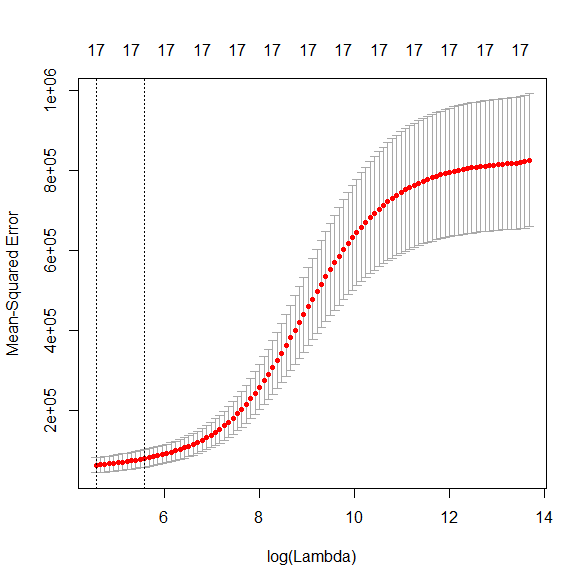
MSEP(Y軸)が最も小さい値を確認する。
左側の縦破線が通っている赤いドットのY軸値。
> min(ridge.res.cv$cvm)
[1] 61345.74
MSEP が最も小さいときの λ と $\log (\lambda) $ を確認する(左側の縦破線のX軸値)。
> ridge.res.cv$lambda.min
[1] 95.77041
> log(ridge.res.cv$lambda.min)
[1] 4.561954
MSEP が最も小さいときの λに対応した回帰係数を確認する。
> coef(ridge.res.cv, s="lambda.min")
18 x 1 sparse Matrix of class "dgCMatrix"
1
(Intercept) 2.234662e+02
Private -7.114514e+01
Apps 1.738649e-02
Accept 1.106883e-01
Top10perc 2.040518e+00
Top25perc -3.542996e-01
F.Undergrad 1.035560e-01
P.Undergrad 8.384248e-03
Outstate -4.248129e-03
Room.Board -3.121038e-02
Books 2.823821e-02
Personal 1.564955e-02
PhD 5.052552e-01
Terminal 2.447818e-02
S.F.Ratio 2.254079e+00
perc.alumni 1.854235e+00
Expend -2.158011e-04
Grad.Rate 1.225929e-01
学習データでMSEPが最も小さいときの λ のモデルをテストデータに適用する。
ridge.test.cv <- predict(ridge.res.cv, s="lambda.min", newx=data.matrix(College[-sub,-4]))
mean((ridge.test.cv-College[-sub,]$Enroll)^2)
テストデータの予測値と実測値のかい離を MSEP で求める。
> mean((ridge.test.cv-College[-sub,]$Enroll)^2)
[1] 44719.1
学習データの MSEP は、以下の通り。
> min(ridge.res.cv$cvm)
[1] 61345.74
テストデータの MSEP のほうが小さくなっているのがわかる。
予測性能がよいことを示している。
ラッソで解析した結果
glmnet()でalpha=1と指定する。
最初からクロスバリデーションを使う。
lasso.res.cv <- cv.glmnet(data.matrix(College[sub,-4]), College[sub,]$Enroll, alpha=1)
plot(lasso.res.cv)
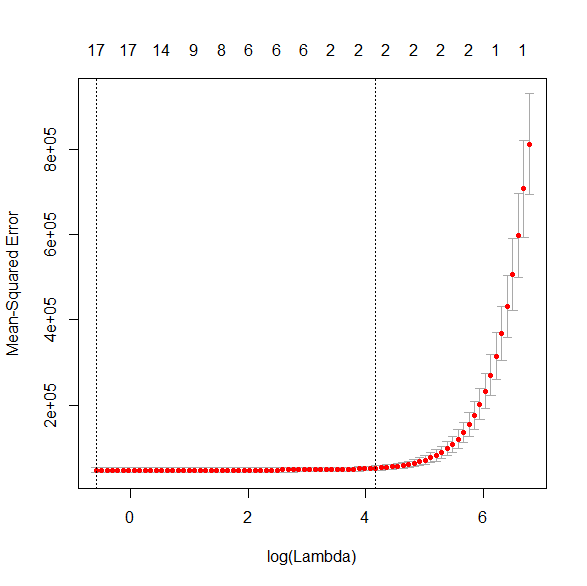
MSEP が最小値を表示させる(Y軸)。
MSEP が最小値の $ \log (\lambda) $ を表示させる(X軸)。
MSEP 最小値の λ のときの回帰係数を表示させる。
> min(lasso.res.cv$cvm)
[1] 46512.83
> log(lasso.res.cv$lambda.min)
[1] -0.5781604
> coef(lasso.res.cv, s="lambda.min")
18 x 1 sparse Matrix of class "dgCMatrix"
1
(Intercept) 223.249334574
Private -17.323492035
Apps -0.034361012
Accept 0.152731795
Top10perc 3.758399461
Top25perc -1.812982422
F.Undergrad 0.142965370
P.Undergrad -0.029337386
Outstate -0.003177355
Room.Board -0.018717120
Books 0.012830680
Personal -0.003259145
PhD 0.191660710
Terminal -1.050251664
S.F.Ratio -0.547854820
perc.alumni 1.834686143
Expend 0.001059255
Grad.Rate 0.177922346
学習データでもっともすぐれたモデルで、テストデータ予測をする。
MSEP を計算する。
lasso.test.cv <- predict(lasso.res.cv, s="lambda.min", newx=data.matrix(College[-sub,-4]))
mean((lasso.test.cv-College[-sub,]$Enroll)^2)
> mean((lasso.test.cv-College[-sub,]$Enroll)^2)
[1] 46711.87
学習データでの MSEP とほぼ同じ値。
以下が、学習データでの MSEP の値。
> min(lasso.res.cv$cvm)
[1] 46512.83
大きく増加しているわけではないので、予測に使えなくはない。
エラスティックネットの結果
0 < α< 1 がエラスティックネットだ。
リッジとラッソの中間で、いいとこどりの方法。
α を振って試してくれる関数が glmnetUtils パッケージの cva.glmnet() だ。
最初一回だけインストールする。
使うときはlibrary()で呼び出す。
install.packages("glmnetUtils")
library(glmnetUtils)
cva.glmnet() は cv.glmnet() と書き方は一緒。
α はデフォルトで11個に振ってくれる。
elnet.res.cv <- cva.glmnet(data.matrix(College[sub,-4]), College[sub,]$Enroll)
plot(elnet.res.cv)
$ \log (\lambda) $ とMSEPのプロットは以下の通り。
αが11個に振られているので、11本のグラフになる。
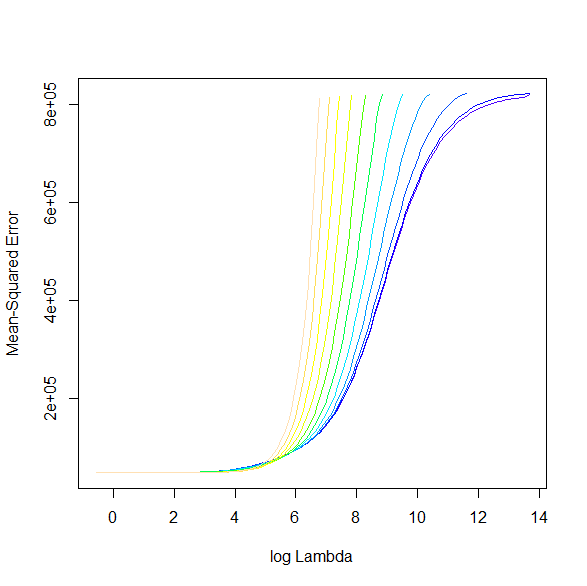
αを確認すると以下の通り。
> elnet.res.cv$alpha
[1] 0.000 0.001 0.008 0.027 0.064 0.125 0.216 0.343 0.512 0.729 1.000
最適な α を選ぶため MSEP がもっとも小さい α を探す。
各 α のうち最も小さい MSEP を取りだし、その中でもっとも小さいMSEPを取り出したところ、α = 1 がもっとも MSEP が小さかった。
つまり、ラッソがもっとも当てはまりがよいモデルであった。
> sapply(sapply(elnet.res.cv$modlist, "[[", "cvm"),min)
[1] 61274.57 61208.48 47948.64 47276.72 47268.60 47292.46 47324.64 47347.99 47177.38
[10] 47006.23 46913.66
> min(sapply(sapply(elnet.res.cv$modlist, "[[", "cvm"),min))
[1] 46913.66
α = 1 のときの、MSEP が最小になる λ のモデルを使って、テストデータで予測する。
elnet.test.cv <- predict(elnet.res.cv, alpha=1, s="lambda.min", newx=data.matrix(College[-sub,-4]))
mean((elnet.test.cv-College[-sub,]$Enroll)^2)
MSEP は学習データよりも小さくなり、予測性能が高いと言える。
> mean((elnet.test.cv-College[-sub,]$Enroll)^2)
[1] 45275.5
まとめ
学習データに当てはまりすぎない、予測性能に優れたモデルを作る、リッジ、ラッソ、エラスティックネットを紹介した。
リッジがいいか、ラッソがいいか、は、エラスティックで α を振ってみて、選ぶのがよい。
glmnetUtils パッケージの cva.glmnet() は痒いところに手が届く関数で使いやすい。









コメント