R で傾向検定を行う方法

2018年6月29日2024年10月14日

傾向検定は、サンプルデータで観察された、平均値や割合が、だんだんに大きくなる、だんだんに小さくなるという傾向が、母集団でもその通りか検定するもの。

Rでどのようにやるかまとめてみた。

＞＞もう統計で悩むのは終わりにしませんか？

↑期間・数量限定で無料プレゼント中！

単変量の傾向検定：コクラン・アーミテージ検定

回答の選択肢に方向性がある場合の検定は？

クロス集計表の検定を行いたいと思ったが、

サイズのS,M,Lとか、
好みの好き、少し好き、少し嫌い、嫌いとか、
年齢の20代、30代、40代、50代、60代以上とか、
だんだんに大きくなるとか、
だんだんに小さくなるとか、

方向性がある場合、$ \chi^2 $（カイ2乗）検定でいいのか？

という疑問に突き当たることがある。

実は、$ \chi^2 $ 検定よりも、適切で、しかも、統計学的有意が出やすい方法がある。

それが傾向（トレンド）検定の、コクラン・アーミテージ検定。

$ \chi^2 $ 検定だとトレンドは見ることはできない。

どこかのカテゴリが他と違うとしかわからない。

コクラン・アーミテージ検定は、トレンドを検出する。

だんだんに多くなる、だんだんに少なくなるを感知する。

選択肢の方向性がある場合の回答の傾向性つまりトレンドを確認する。

コクラン・アーミテージ検定を R で行うには？

prop.trend.test()を使う。

変数の各カテゴリのYesの人数をxとする。

各カテゴリの人数全体をnとする。

割り当てるスコアを決める。

4カテゴリが「好き、少し好き、少し嫌い、嫌い」だとすると、そこに１，２，３，４とスコアをあてはめる。

x <- c(44,55,65,78)
n <- c(95,120,129,132)
score <- c(1,2,3,4)

計算スクリプトはいたってシンプルだ。

prop.trend.test(x,n,score)

計算してみると、以下のようになる。

> prop.trend.test(x,n,score)
Chi-squared Test for Trend in Proportions
data:  x out of n ,
using scores: 1 2 3 4
X-squared = 4.5998, df = 1, p-value = 0.03198

p値を見ると、0.05未満で、統計学的有意。

統計学的有意にYesの割合にトレンドあり。

各カテゴリのYesのパーセンテージを計算すると、

以下のようになり、だんだんに大きくなっている。

> round(x/n*100)
[1] 46 46 50 59

生データからコクラン・アーミテージ検定をするには？

R のfunctionを使って、生データ（raw data）からコクラン・アーミテージ検定ができるようにしてみた。

xにカテゴリデータ、yにYes/Noデータを入れれば解析できる。

my.cochran.armitage <- function(x,y,colnum=1){
tab.xy <- table(x,y)
rownum <- nrow(tab.xy)
if (ncol(tab.xy) > 2) {stop("You have to use Yes/No (1/0) data in the Column")}
else {print(prop.trend.test(tab.xy[,colnum], tab.xy[,1]+tab.xy[,2], c(1:rownum)))}
}

多変量解析の傾向検定：ロジスティック回帰

多変量調整しながら、カテゴリ変数の影響を見たい場合。

ロジスティック回帰モデルを使う。

ロジスティック回帰でカテゴリのトレンドを見る場合

5カテゴリあるとする。

１，２，３，４，５と変換する。

連続量として投入する。

カテゴリで投入すると、１のカテゴリを基準として２，３，４，５のオッズ比が算出できる。

１から５を数値のままで投入したらどうなるか。

１から５を連続量とみて、推定値が一つ計算される。

それが統計学的有意なら、トレンドが有意。

カテゴリ間が1でいいのか？

カテゴリ間が1であるのはなぜか？

カテゴリ間が1である保証は？

という難しい問題はあるが。。。

ロジスティック回帰でもともと連続量だった変数の傾向検定

5カテゴリがもともと連続量だったとする。

年齢区分で、20代、30代、40代、50代、60代とか。

こういう場合、各カテゴリの真ん中を当てるという方法がとられる。

この場合は、25、35、45、55、65とするわけだ。

これを疑似連続量と考えて、そのままモデルに投入する。

推定値が統計学的有意かどうかで、トレンドが有意かどうかが判断できる。

有意なら、もとの連続量で投入してもいい。多変量モデルに投入する変数を減らせるので好都合。

＞＞もう統計で悩むのは終わりにしませんか？

↑1万人以上の医療従事者が購読中

平均値の傾向検定はどうやるか？

ANOVAの関数 aov() とmultcompパッケージの glht() を使って実施する。

multcompパッケージは一回だけインストールする。

install.packages("multcomp")

使うときに呼び出す。

library(multcomp)

warpbreaksデータを使ってやってみる。

contrasts=で検定方法を決めている。

tensionはL, M, Hの3カテゴリで、3カテゴリの推定値と1, 0, -1というベクトルが直線的に相関しているかどうかをみて、トレンド検定としている。

一緒にLだけ違うという仮説も検証している。

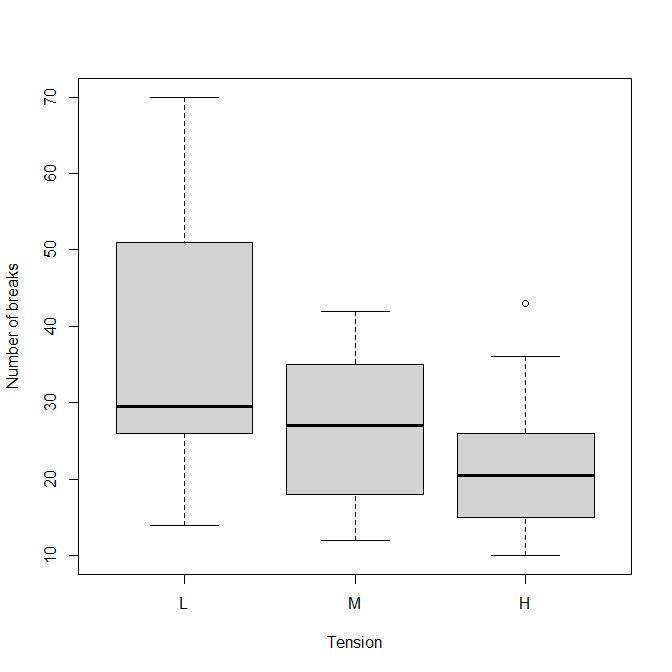
boxplot(breaks ~ tension, data=warpbreaks, xlab="Tension", ylab="Number of breaks")
aov.res <- aov(breaks ~ tension, data=warpbreaks)
contr <- rbind("linear trend" = c(1,0,-1), "L!=M|H" = c(2,-1,-1))
glht.res <- glht(aov.res, linfct = mcp(tension = contr))
summary(glht.res)

トレンド検定（linear trend）もLだけ違うという仮説も、ともに統計学的に有意という結果になった。

箱ひげ図から考えれば、だんだんに減っていくという仮説のほうがより適切と思う。

> summary(glht.res)
Simultaneous Tests for General Linear Hypotheses
Multiple Comparisons of Means: User-defined Contrasts
Fit: aov(formula = breaks ~ tension, data = warpbreaks)
Linear Hypotheses:
Estimate Std. Error t value Pr(>|t|)
linear trend == 0   14.722      3.960   3.718 0.000827 ***
L!=M|H == 0         24.722      6.859   3.604 0.001166 **
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Adjusted p values reported -- single-step method)