2025年– date –
-

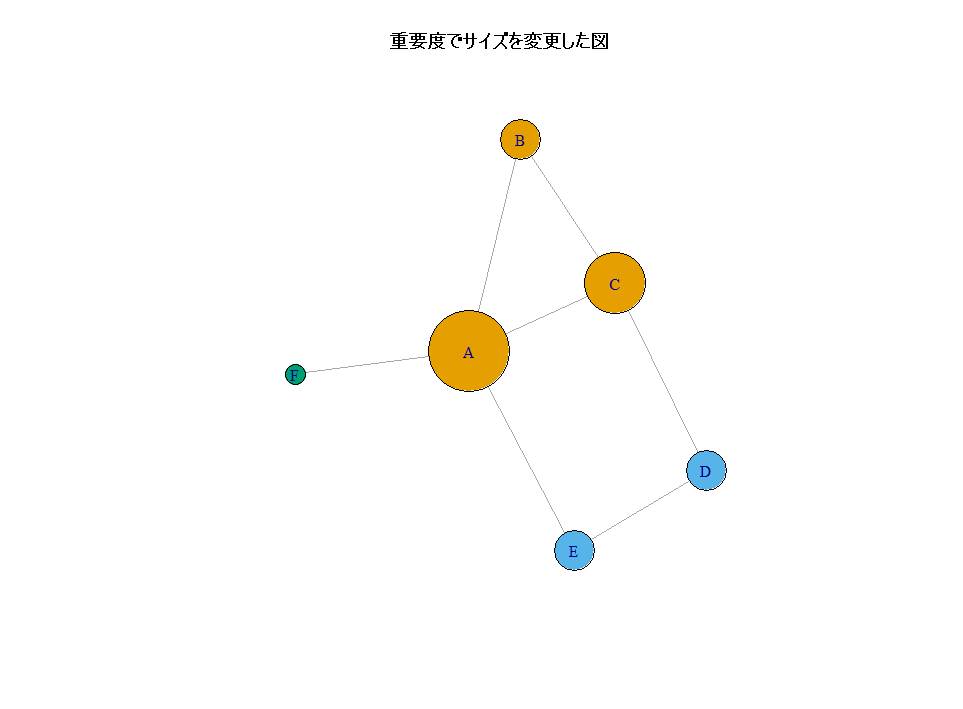
Rのigraphで始める!ネットワーク分析入門:データの準備から可視化のコツまで
SNSのつながり、仕事の人間関係、単語の結びつきなど、複雑な関係性を目に見える形にしたいと考えたことはないだろうか。 そんな時、R言語で最も頼りになるのがigraphパッケージである。この記事では、Rを使い始めたばかりの読者に向けて、igraphの基本か... -

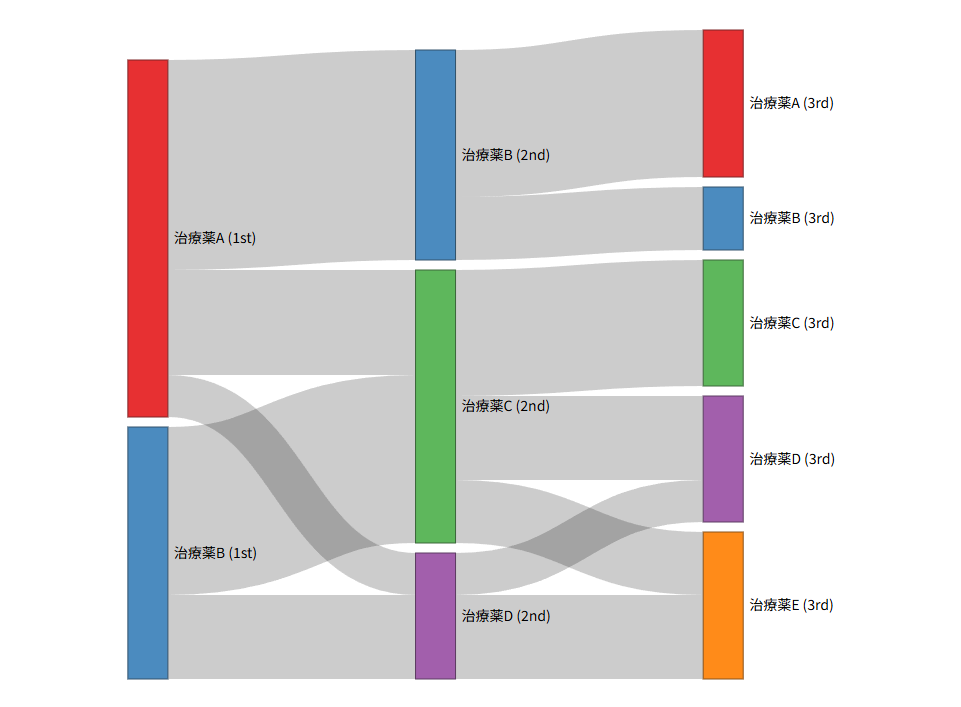
サンキーダイアグラムで治療の遷移を可視化する:Rによる作成ガイド
「1次治療から2次治療へ、患者はどのように遷移しているのか?」 「どのタイミングで治療の切り替え(スイッチ)が多く発生しているのか?」 医療データや臨床研究の結果を報告する際、こうした「流れ」の把握は極めて重要である。そこで威力を発揮するの... -

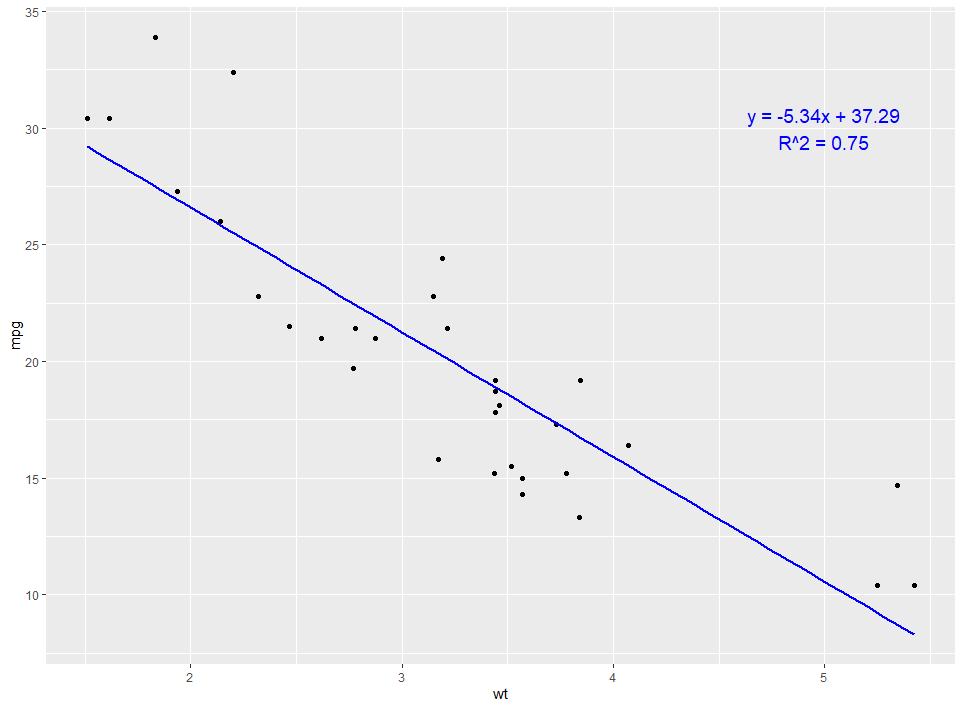
ggplot2の図にテキストを書き入れる方法:目的別の使い分けと実践コード
Rのggplot2を使ってグラフを作成している際、「特定のデータ点に名前を入れたい」「グラフの余白に補足説明を追加したい」と考えたことはないだろうか。 グラフは視覚的にトレンドを伝えるのが得意だが、「言葉(テキスト)」を添えることで、読み手の理解... -

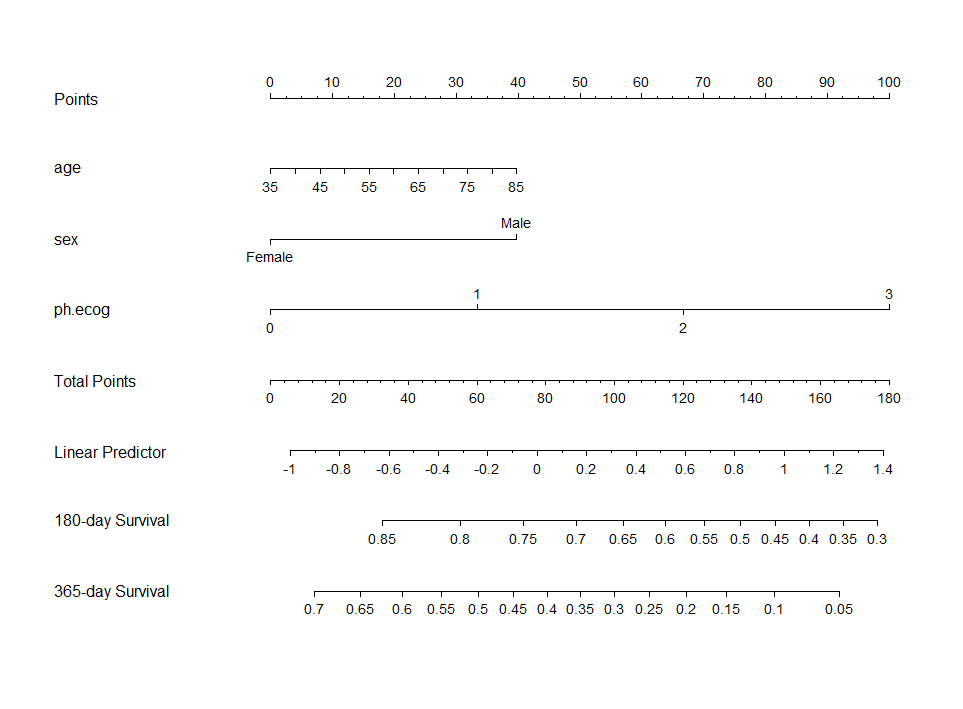
ノモグラムの作成方法完全ガイド:RでのCox回帰モデル実装から活用法まで
「統計解析の結果を、もっと直感的に伝えたい」と思ったことはないだろうか。 複雑な回帰分析の結果を、定規1本で計算できるグラフに変換してくれるのが「ノモグラム(Nomogram)」である。本記事では、ノモグラムの基礎から、Rを使った具体的な作成方法、... -

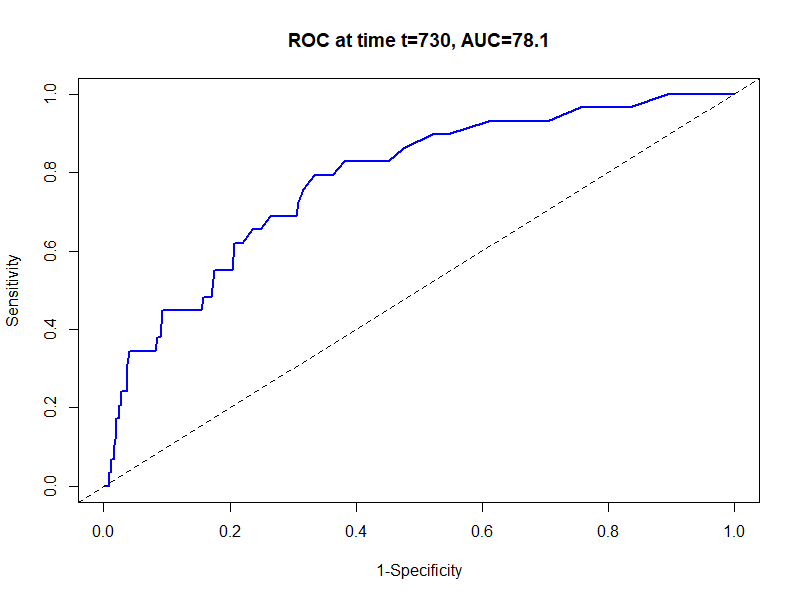
生存分析の予測精度を評価する「時間依存性ROC曲線」:Rでの実装まで解説
医療統計やデータ分析において、予測モデルの精度を評価する際に「ROC曲線」は欠かせない指標である。しかし、生存時間解析のように「時間の経過」が関わるデータでは、通常のROC曲線だけでは不十分な場合が多い。 そこで用いられるのが「時間依存性ROC曲... -

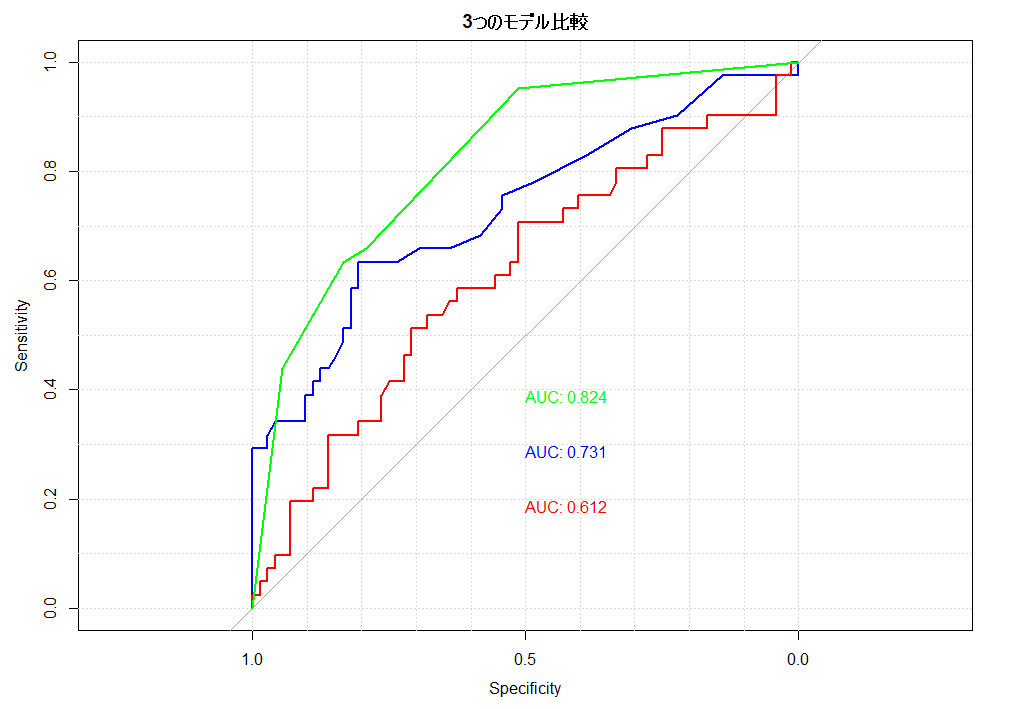
Rで実践:3つ以上のROC曲線を1つのグラフにまとめる手法
医療統計や機械学習において、複数の予測モデルの性能を比較する際、ROC曲線(受信者動作特性曲線)を1つのグラフに重ねて描画することは、視覚的な評価において極めて重要である。 本記事では、Rの標準的なパッケージであるpROCを用い、1本から3本、さら... -

ロジスティック回帰モデルの評価指標:混同行列からROC曲線、Youden Indexまで
ロジスティック回帰モデルを構築した後、多くの初心者は「正解率(Accuracy)」のみを見てモデルの良し悪しを判断しがちである。しかし、分類タスクにおいて正解率のみを指標とすることは、時として重大な判断ミスを招く。 本記事では、モデルの性能を多角... -

その数値は本当に正しいか?検査機器の妥当性を評価する「R²」と「Bland-Altmanプロット」の使い分け
新しい検査機器を導入する際、最も重要なプロセスは「その機器がどれだけ正確か」を客観的に証明することである。しかし、ここで多くの人が陥る罠がある。それは「相関関係(R²)さえ高ければ、機器の性能は十分である」と思い込んでしまうことだ。 本記事... -

アンバランスな2群のサンプルサイズ計算ガイド:平均・割合・生存率のケース別解説
実務で統計を扱っていると、「比較したい2つのグループの人数がどうしても同じにならない」という場面に頻繁に遭遇する。例えば、希少疾患の治験で「新薬群」の患者確保が難しかったり、Webマーケティングで「新デザイン」をリスク回避のために一部のユー... -

時間の計算方法 一筋縄ではいかない時間の計算
ある時点からある時点までの日数や時間を計算したい場面は多い。しかし、計算の目的が「日数」なのか「時間」なのかによって、データの準備の仕方は異なる。特に時間は「60進法」や「日をまたぐ処理」があるため、単純な数値の引き算では失敗しやすい。 本... -

回帰分析の結果の書き方:数値の意味から記述例まで解説
回帰分析の結果をレポートやブログにまとめる際、どの数値を拾い、どう表現すべきか。本記事では、初心者が必要最低限押さえるべきポイントを簡潔に解説する。 結果として表示する数値 分析ソフトの出力結果から、まず以下の3点を確認する必要がある。 偏... -

サンプルサイズが小さい研究における論文執筆のポイント:有意差が出なかった際の考察法
研究計画を立てる際、理想的なサンプルサイズを確保できるケースばかりではない。特に希少な事象を扱う場合や、探索的な研究では、どうしても小サンプルにならざるを得ない状況がある。その際、多くの研究者が直面するのが「統計学的有意差が出ない」とい... -

リッカート尺度は「平均」を出してもいい?連続データとして扱う根拠と注意点
アンケート調査で頻繁に使われる「非常に満足」から「非常に不満」までの5件法。これを統計解析の際に「平均値」を出せる連続データとして扱ってよいのか、迷う実務者は多い。 厳密に言えば、リッカート尺度は順序を付けただけの「順序尺度」である。しか... -

線形回帰の罠:なぜ「データの正規性」は必須ではないのか
統計学やデータ分析の初学者が線形回帰を学ぶ際、最初につまずくポイントがある。それが「正規性の仮定」だ。「分析対象のデータ(目的変数)が正規分布していなければ、回帰分析は使えない」と思い込み、分析を断念したり、無理なデータ変換を繰り返した... -

IPTWと共変量で調整する二重ロバスト推定:初心者向け解説
統計解析において「より正確な因果関係」を導き出すための強力な手法が、二重ロバスト推定(Doubly Robust Estimation)である。一見難解に思えるが、その仕組みは非常に合理的で「保険」をかけた解析手法と言える。 本記事では、初心者でも流れが掴めるよ... -

IPTWは何を目的に何をしているのか:ざっくりとした説明
新しい薬の効果を確かめたいとき、あるいは特定のマーケティング施策が売上に貢献したかを知りたいとき、理想的なのは「くじ引き」で対象者を分けることである。しかし、現実のデータ(観察データ)では、健康意識の高い人ほど薬を飲みがちであったり、特... -

R言語を独学でマスターする ― おすすめ書籍5選と学習のコツ
データ分析の必要性に迫られ、何から手をつければいいか迷っている方は多い。 「EZRやRコマンダーなどのGUIツールは使っているが、より自由度の高い解析を行いたい」 「統計ソフトのブラックボックスを脱し、自分の意図通りにデータを制御したい」 本記事... -

統計学の落とし穴?「前提確認の検定」を避けるべき理由と正しい向き合い方
データ分析を行う際、「正規分布しているか?」「分散は等しいか?」と、手法を選ぶための「予備テスト(前提確認)」を行っていないだろうか。実は、この予備テストの結果を見てから本番の検定手法を選択する行為は、統計的な誤りを生む原因となる。本記... -

アウトカムを最もよく予測するカットオフをROC曲線分析で見極めて、アウトカムを予測する回帰分析を行うことの是非
医療や疫学研究において、検査値のような連続データを「異常/正常」に区切るカットオフ値の設定は必須である。このカットオフ値を決定する強力な手法がROC曲線分析である。しかし、「ROC分析で最適化したカットオフ値を用いて二値化し、その結果をさらに回... -

連続データのカットオフ値の問題点:なぜ安易に区切ってはいけないのか
血圧を「高血圧」と「正常」に区切る130mmHgの壁、優良顧客と一般顧客を分ける100万円の売上ライン――私たちは連続的なデータを、わかりやすくするために特定のカットオフ値で二分しがちである。この単純化は、一見すると意思決定を迅速にする便利なツール... -

オッズ比とリスク比の違いを徹底解説
疫学研究や医療統計の論文には、「オッズ比(Odds Ratio: OR)」と「リスク比(Risk Ratio: RR)」、すなわち「相対危険(Relative Risk: RR)」が頻繁に登場する。これらはどちらも「ある要因が疾病や事象の発生にどれくらい影響するか」を示す指標である... -

交絡因子調整とは何か:初心者でもわかるデータ分析の基本
「あの薬を飲んだ者は、飲まなかった者より病気が治る割合が高い」――このような研究結果を聞いたとき、あなたは素直に「その薬が効いたのだ!」と信じるだろうか。 実は、データの世界では、二つの事象(例:薬の服用と病気の回復)の間に見かけ上の関連が... -

説明変数の選び方:統制すべき共変量に関するまとめ
統計的分析、特に「ある行動(処置)が、どのような結果(アウトカム)をもたらすか」を知りたい因果推論を行う際、どの変数をモデルに入れるか(=説明変数として統制するか)は非常に重要である。 間違った変数を選んでしまうと、せっかくの分析が台無し... -

データの「見えない値」をどう扱う?検出限界以下(ND)の値の正しい対処法
実験や分析でデータを得た際、「検出限界以下(Not Detected: ND)」という結果に直面したことがあるだろう。これは、物質が存在する可能性はあっても、測定機器では捉えられなかったことを意味する。 これらの「見えない値」を無視して「0」と入力したり... -

IPTWを用いた回帰モデル:なぜ標準誤差の推定がそんなに重要なのか?
因果推論の分野では、観察研究からバイアスの少ない効果を推定するために様々な手法が用いられる。その中でも、Inverse Probability of Treatment Weighting(IPTW)は、共変量の不均衡を調整し、治療群と対照群を「比較可能」にする強力なツールである。I... -

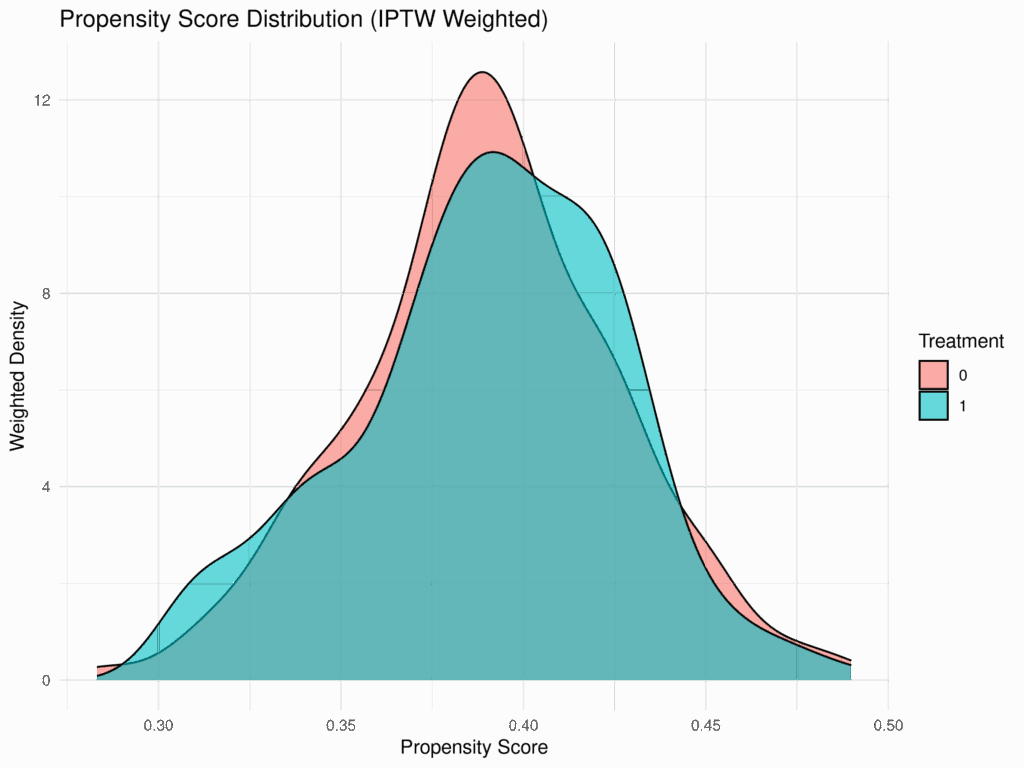
Rで作成するIPTWベースラインサマリー表:tableone とその他関数を使いこなす
疫学研究や臨床研究において、観察研究で因果推論を行う際には、治療群間の共変量バランスが取れていないことが大きな課題となる。この課題を解決するための強力な手法の一つが、IPTW (Inverse Probability of Treatment Weighting) である。IPTWを用いる... -

逆確率重み付け(IPTW)を用いた治療効果の推定:因果推論の基本と実践
「あの治療を受けていたら、どうなっていたのだろう?」多くの人が一度は抱く疑問だろう。医学研究や社会科学において、特定の介入(治療、政策、プログラムなど)がもたらす効果を正確に知ることは非常に重要である。しかし、現実の世界では、誰がどの介... -

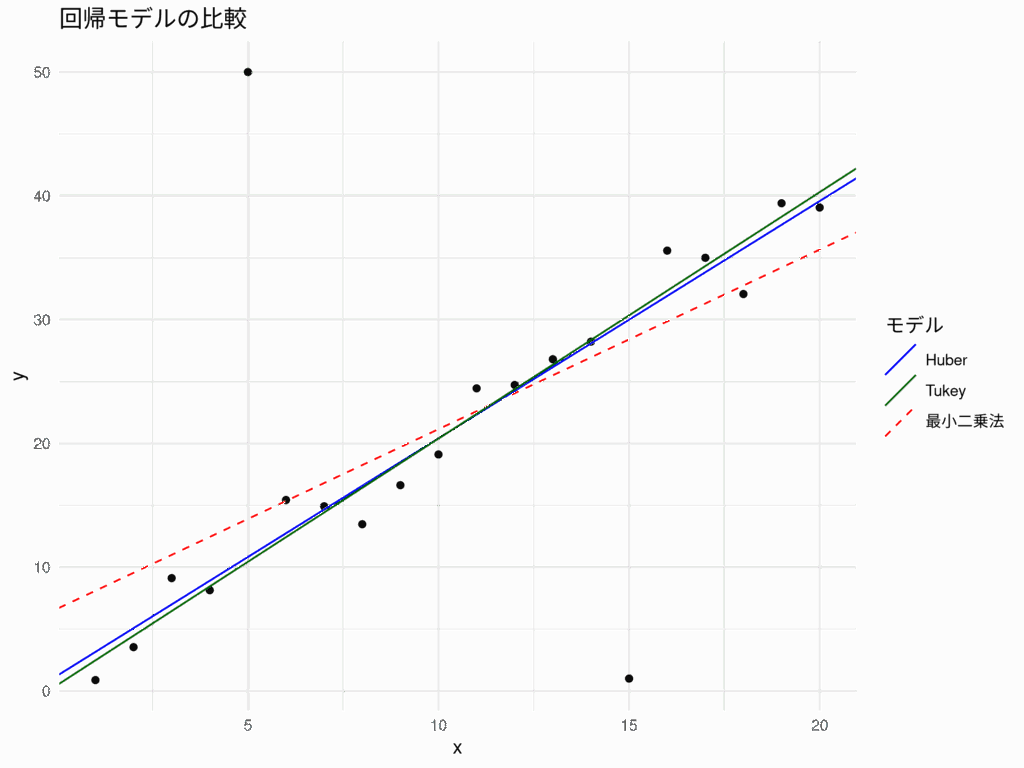
回帰分析におけるロバスト推定法:外れ値に強いモデルを構築する
回帰分析は、変数間の関係性を明らかにする強力な統計ツールである。しかし、データの中に「外れ値」と呼ばれる特異な値が存在する場合、通常の最小二乗法では分析結果が大きく歪められてしまうことがある。このような問題を解決し、より信頼性の高いモデ... -

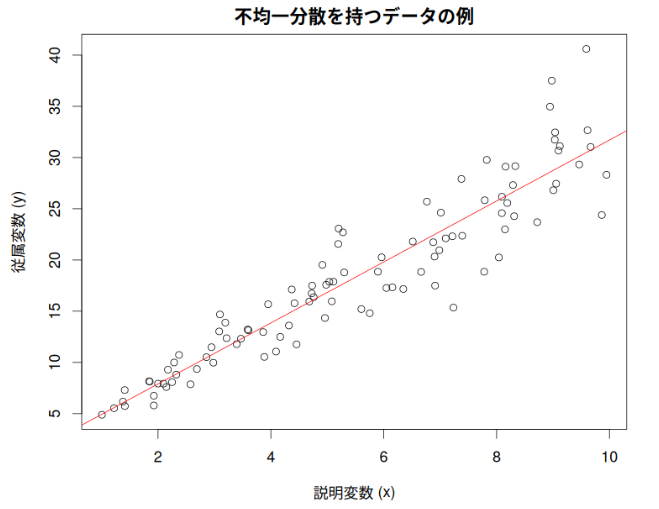
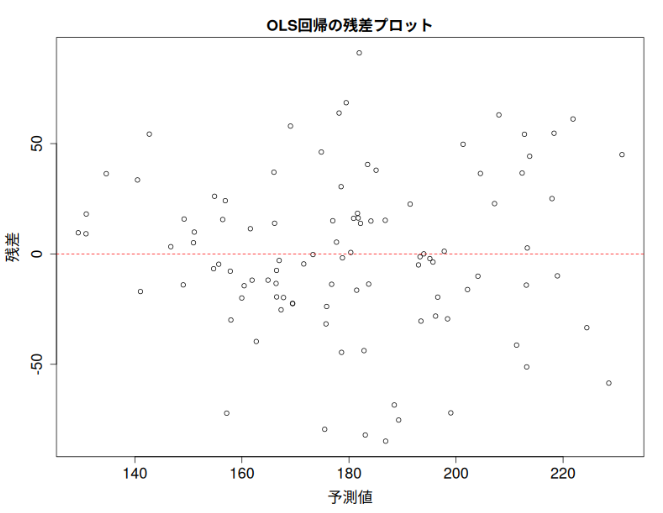
不均一分散とその対処法:統計モデリングをより頑健にするために
統計モデリングを行う際、データの「分散」が均一であるという仮定を置くことがよくある。しかし、現実のデータではこの仮定が成り立たない、つまり「不均一分散」を示すケースが少なくない。不均一分散は、統計的推論の信頼性を損なう可能性があり、適切... -

重回帰分析における重み付き最小二乗法:データの潜在的な声を聴く
重回帰分析は、複数の説明変数を用いて目的変数を予測する強力な統計手法である。しかし、OLS(Ordinary Least Squares:通常の最小二乗法)を適用する際に、ある重要な仮定が満たされない場合、そのモデルの信頼性が損なわれることがある。それが「等分散... -

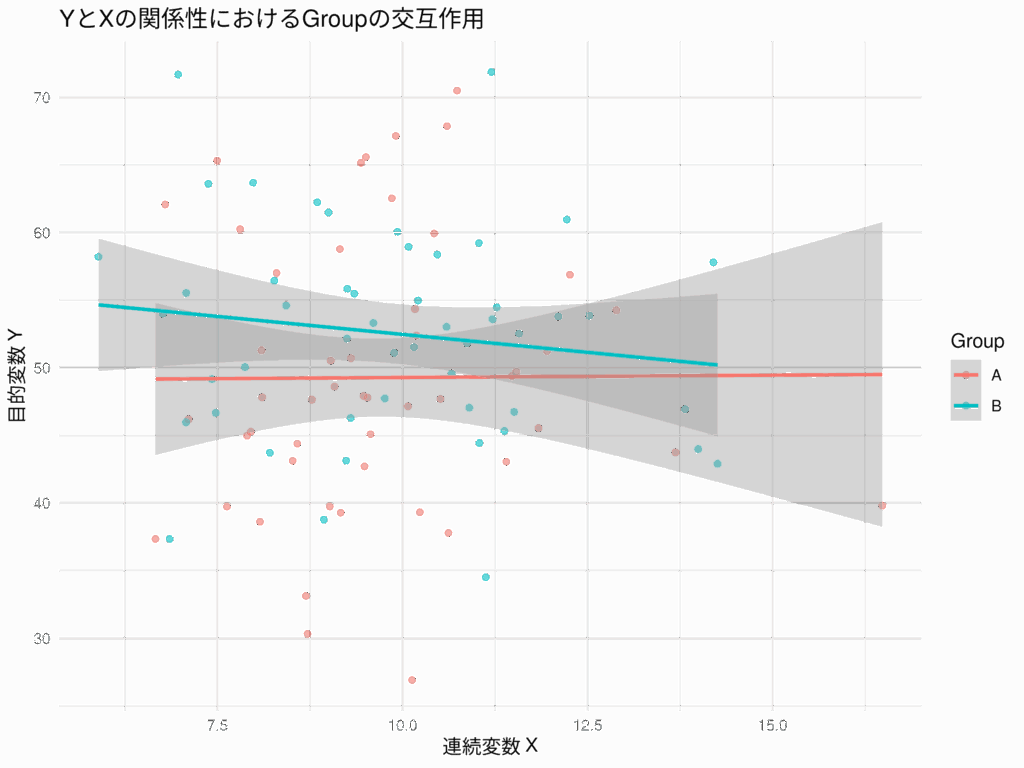
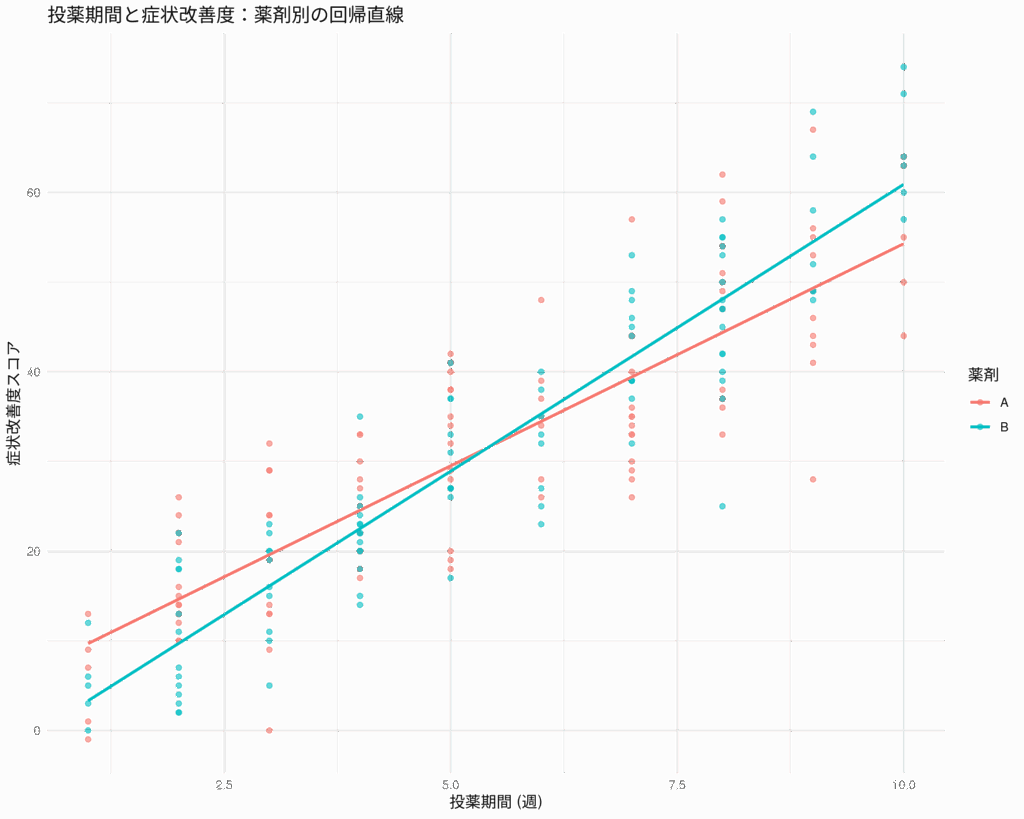
交互作用項のある回帰分析:有意な交互作用とサブグループ解析の記述方法
回帰分析を行う際、2つ以上の説明変数が従属変数に与える影響が、互いの水準によって異なる場合がある。このような現象を「交互作用(interaction)」と呼び、統計モデルに交互作用項を組み込むことで、より詳細な関係性を明らかにできる。 しかし、交互作... -

偏相関の二乗:その概念からRでの実践まで徹底解説!
この記事では、統計分析で重要な役割を果たす「偏相関の二乗」について掘り下げる。この指標が一体どのような概念であり、どのように計算されるのか、さらにはその異なる呼び名や日本語での表記についても整理する。加えて、具体的な例とRを用いた実践的な... -

重回帰分析と偏相関係数における多重共線性:その影響と対処法
統計分析において、複数の変数間の関係性を探ることは不可欠である。特に、ある結果(目的変数)が複数の原因(説明変数)によってどのように影響されるかを分析する際には、重回帰分析が強力なツールとなる。また、2つの変数間の純粋な関係性を知りたい場... -

交絡因子を考慮した回帰直線の差の検定:より深い洞察を得るために
データ分析において、複数のグループ間での関係性の違いを比較することは非常に重要だ。特に、ある従属変数と独立変数の関係が、別の要因(グループ)によってどのように異なるかを明らかにしたい場合、回帰直線の差の検定は強力なツールとなる。しかし、... -

Rで回帰直線の検定と信頼区間:lm関数を使わずに計算する
単回帰分析では、目的変数と説明変数の間に直線的な関係があるかを調べる。Rのlm関数を使えば簡単に分析できるが、その裏側にある計算ロジックを理解することも重要だ。この記事では、lm関数に頼らずに回帰直線の主要な要素、つまり回帰係数の推定、その検... -

回帰分析の奥深さ:$t$ 値の2乗と$F$ 値が等しい理由を解き明かす!
回帰分析は、変数間の関係性を明らかにする強力な統計ツールだ。その結果を解釈する際、$t$ 値や $F$ 値といった統計量を目にすることが多いだろう。特に、単回帰分析においては、回帰係数の $t$ 値の2乗が、回帰モデル全体の有意性を検定する $F$ 値と常... -

平均値・標準偏差・症例数からt検定を行う:BSDAパッケージのtsum.testを解説
データ分析の現場では、生データが手元になく、要約統計量(平均値、標準偏差、症例数)のみが与えられている状況で統計的検定を行う必要に迫られることがある。特に、2つのグループ間の平均値に有意な差があるかを検証するt検定は頻繁に用いられる。 Rに... -

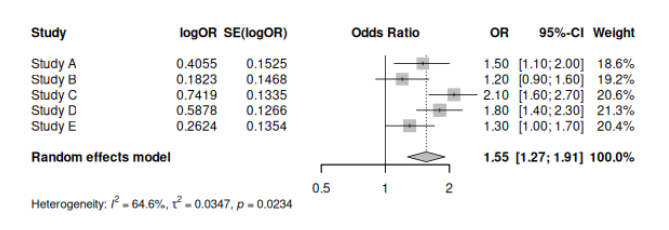
コホート研究のメタアナリシスにおける調整オッズ比と調整ハザード比の統合
コホート研究のメタアナリシスは、複数の独立した研究結果を統合することで、より信頼性の高いエビデンスを導き出す強力な手法である。特に、調整オッズ比 (Adjusted Odds Ratio: AOR) や 調整ハザード比 (Adjusted Hazard Ratio: AHR) のような、交絡因子... -

ベイズの力でエビデンスを統合する:ベイズメタアナリシス徹底解説
複数の研究結果を統合し、より強固なエビデンスを導き出すメタアナリシスは、医療や心理学、社会科学など多岐にわたる分野で重要な役割を果たしている。しかし、従来の頻度論的アプローチでは扱いにくい問題や、事前情報の活用といった点で限界があった。... -

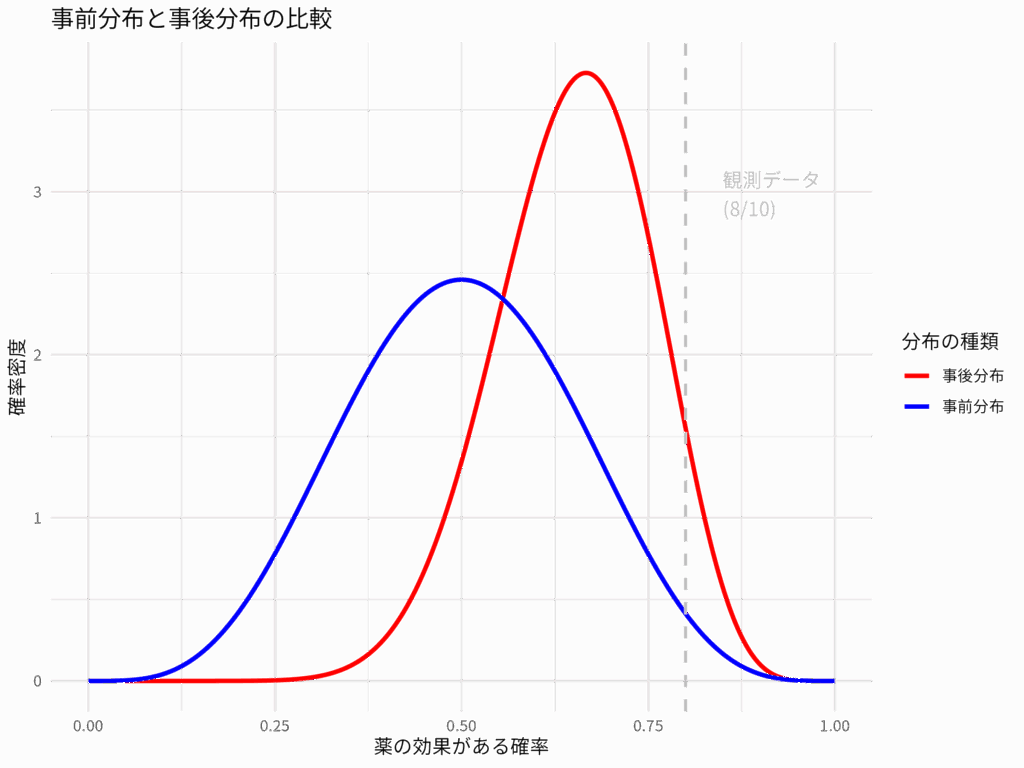
ベイズ統計の核心:事前分布と事後分布を理解する
「データから何かを学ぶ」とき、私たちは常に何らかの「信念」を持っている。ベイズ統計学は、この「信念」をデータに基づいて更新していくという、非常に人間らしい思考プロセスを数学的に表現したものだ。今回は、その中心となる「事前分布」と「事後分... -

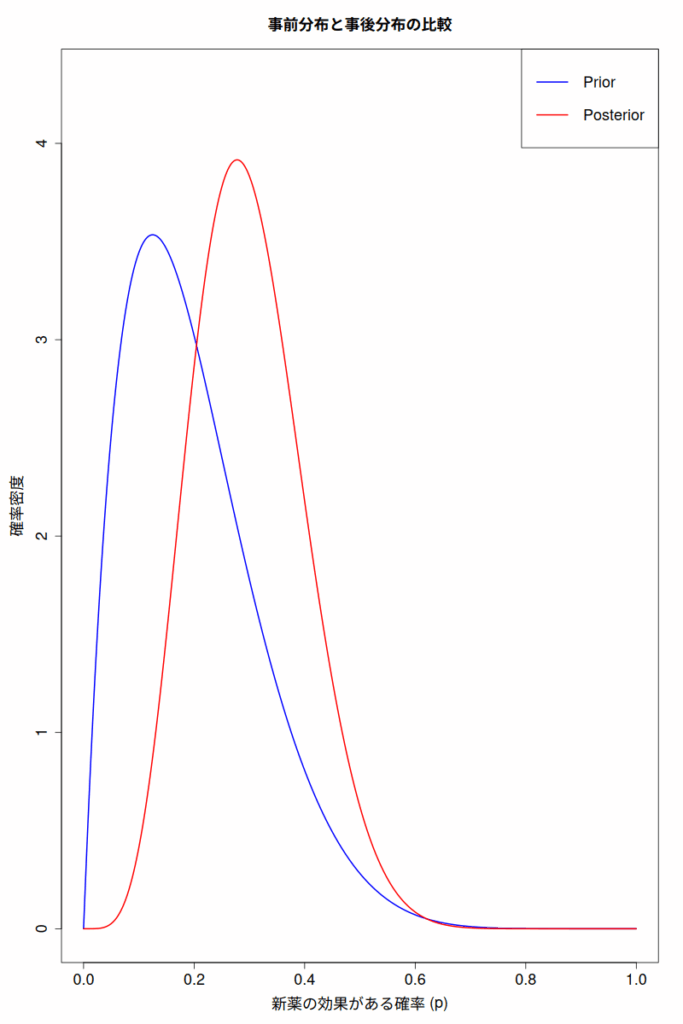
ベイズの理論からベイズ統計へ:不確実性を扱う強力なフレームワーク
私たちが生きる世界は不確実性に満ちている。明日の天気、新しい治療法の効果、マーケティングキャンペーンの成功率など、未来の出来事を完全に予測することはできない。しかし、この不確実性を数学的に捉え、合理的な意思決定を支援する強力なフレームワ... -

ベイズの定理とナイーブベイズ:機械学習の基礎を理解する
機械学習の分野には、様々な強力なアルゴリズムが存在する。中でも特に理解しやすいものの一つがナイーブベイズだ。ナイーブベイズは、あの有名なベイズの定理をベースにしており、スパムメールの分類から医療診断まで、幅広い分野で活用されている。この... -

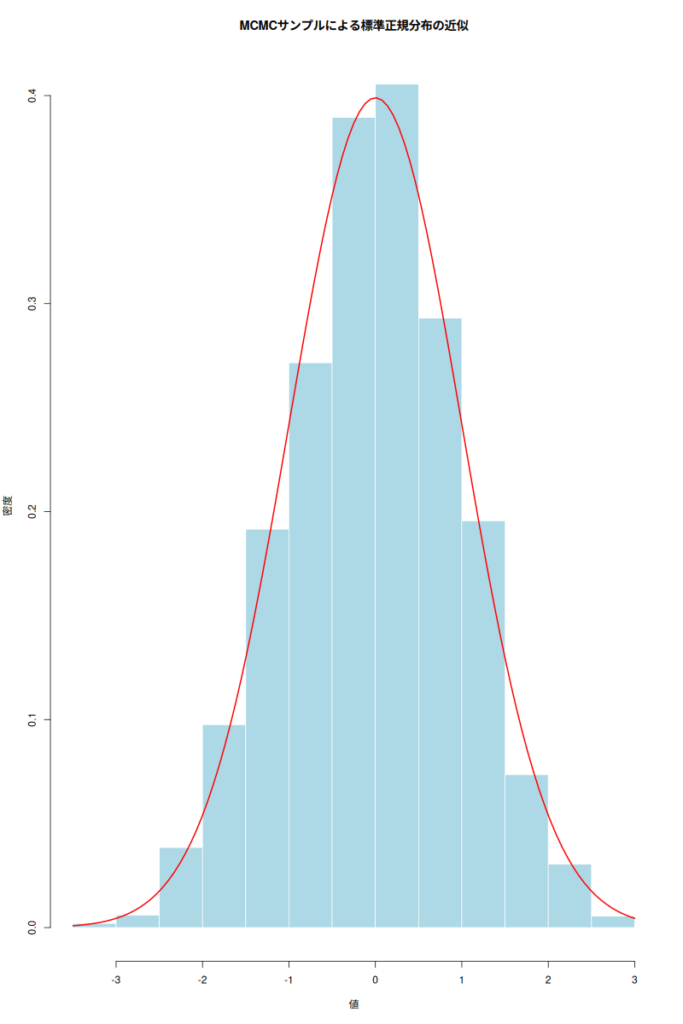
マルコフ連鎖モンテカルロ法 (MCMC) を徹底解説!
「なんだか複雑そうな数式や理論が出てきそう…」そう思われた方もいるかもしれない。しかし、ご安心いただきたい。この記事では、マルコフ連鎖モンテカルロ法 (MCMC) という強力な統計的手法について、その基本から応用までを、できる限りわかりやすく解説... -

ROC曲線における最適なカットオフ値のブートストラップ信頼区間を理解する
医療診断、機械学習の分類問題など、多くの分野でROC曲線はモデルの性能評価に不可欠なツールだ。しかし、ROC曲線から「最適な」カットオフ値を決定するだけでは不十分な場合がある。そのカットオフ値がどの程度信頼できるのか、すなわち、異なるデータセ... -

ブートストラップ因子分析:よりロバストな因子構造を探る
統計分析は奥深く、時には結果の信頼性に疑問を抱くこともある。特に、心理学や社会科学の分野で広く用いられる因子分析は、その性質上、サンプルの変動に影響を受けやすいという側面を持つ。しかし、もしその影響を最小限に抑え、より安定した、信頼性の... -

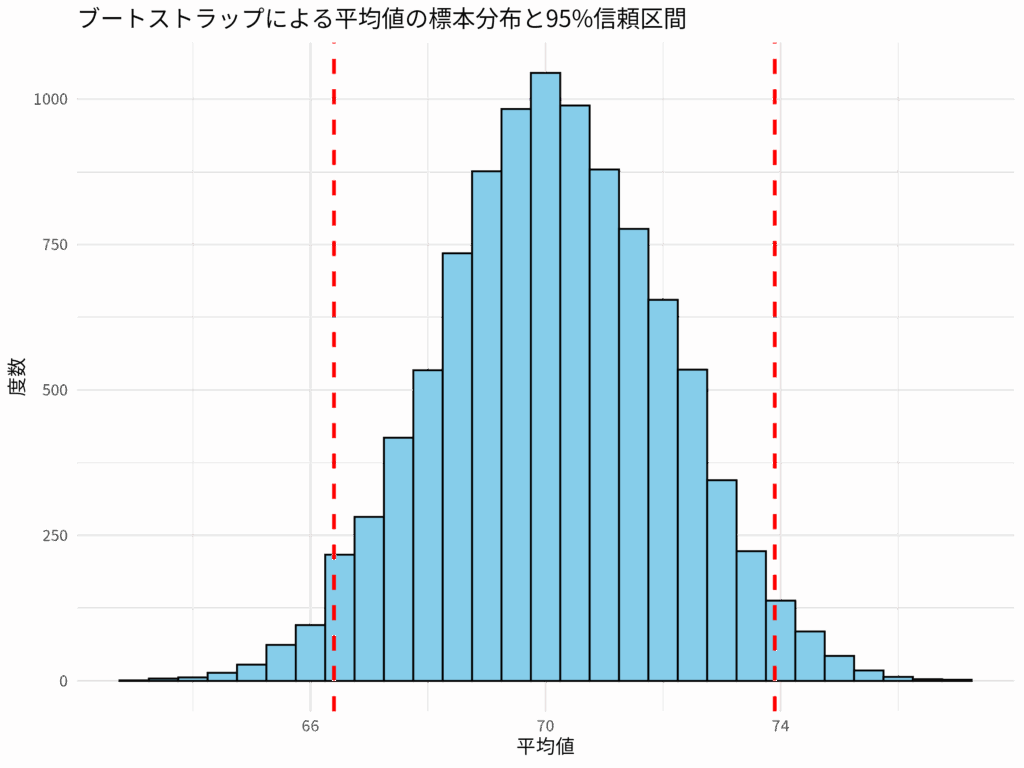
ブートストラップ法で平均値の95%信頼区間を求めよう!
「このデータ、本当に信頼できるのか?」そう思ったことはないだろうか。限られたデータから全体像を推測する際、統計的な「信頼区間」は非常に重要な概念である。しかし、信頼区間を算出するには、データの分布に特定の仮定が必要となるケースが少なくな... -

ブートストラップ法:データの「再利用」で統計的推測を強化する
手元にあるデータだけでは、本当に信頼できる統計的な結論は出せないのではないか?そう悩んだことはないだろうか。特に、データ数が少ない場合や、複雑な統計量に関心がある場合、その悩みは尽きないかもしれない。そんな時に非常に強力なツールとなるの... -

臨床予測モデルの性能比較:最適な評価方法とは?
臨床現場でますます重要性を増している臨床予測モデル。病気の診断、予後の予測、治療効果の推定など、多岐にわたる場面で活用されている。しかし、複数のモデルが存在する場合、どのモデルが最も優れているのか、どのように判断すればよいのだろうか? 本... -

臨床予測モデルの誤設定を避けるために:信頼性の高い予測を目指す
医療現場において、臨床予測モデルは疾患の診断、予後の予測、治療法の選択など、多岐にわたる意思決定を支援する強力なツールである。しかし、これらのモデルが誤って設定された場合、その予測は患者の健康を危険にさらし、医療資源の無駄遣いにも繋がり... -

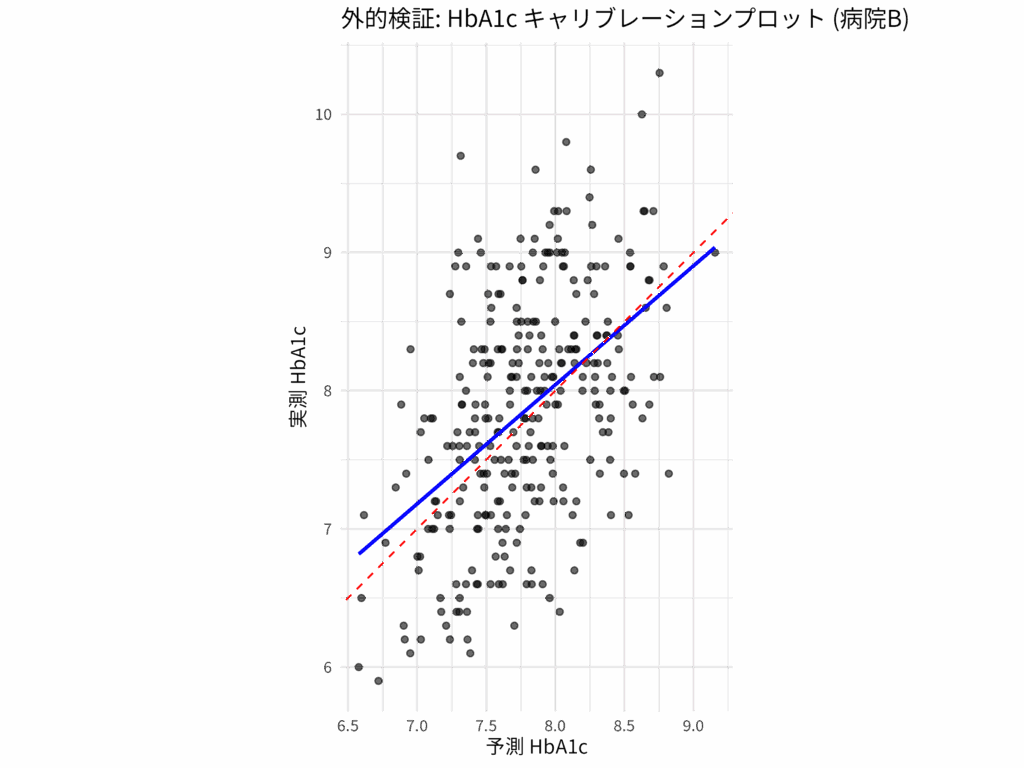
連続アウトカムの臨床予測モデル:予測精度を保証する内的・外的検証
臨床予測モデルは、医療現場で患者の将来を予測する強力なツールだ。特に血圧や血糖値のような連続データをアウトカムとするモデルは、病状の進行予測や治療効果の判定に役立つ。しかし、これらのモデルが実際に役立つためには、その予測能力が信頼できる... -

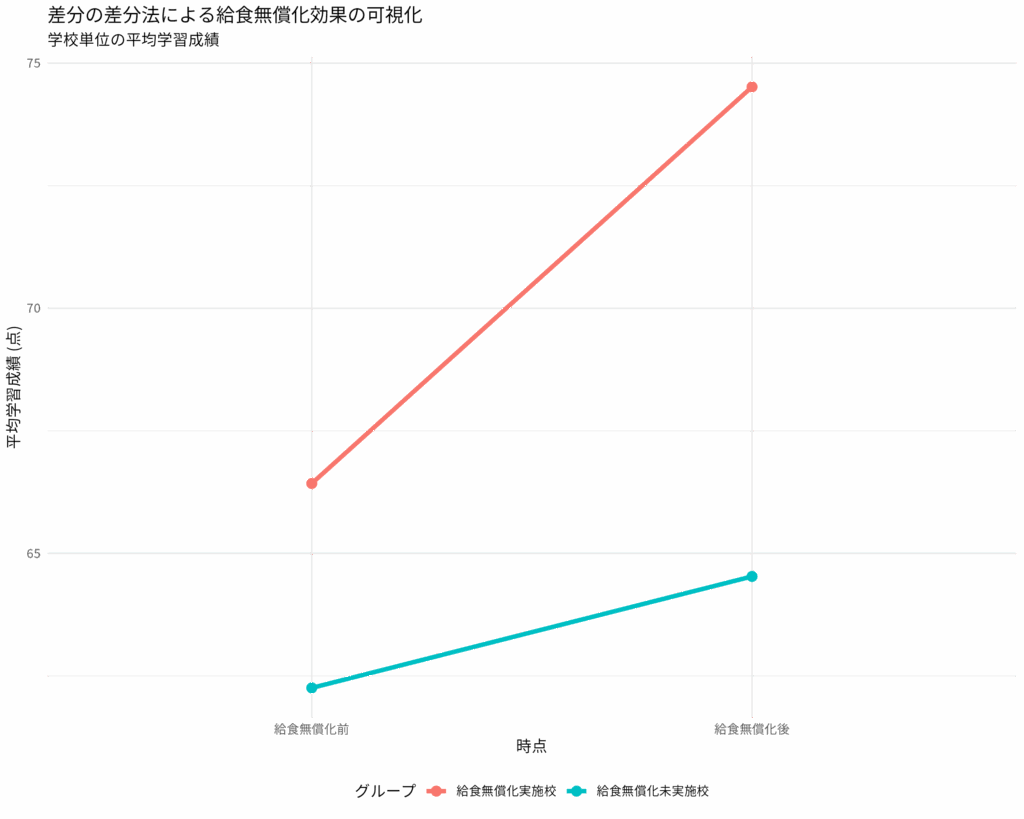
差分の差分法を理解する:因果推論の強力なツール
差分の差分法(Difference-in-Differences, DiD)は、政策変更や介入の効果を評価する際に非常に強力な統計的手法だ。この記事では、DiDの基本的な考え方から、その使い所、関連する統計手法との違い、DiDの核心である並行トレンドの仮定について詳しく解... -

操作変数法を徹底解説!見せかけの相関にだまされないための強力な武器
見せかけの相関に惑わされていないだろうか?世の中には、一見すると関係がありそうに見えて、実はそうではない現象がたくさん存在する。例えば、「アイスクリームが売れるとプールの事故が増える」という話を聞いたことはないだろうか?これは、アイスク... -

SEMにおけるMIMICモデル:潜在変数で測定誤差を考慮した分析を
SEM(構造方程式モデリング)は、心理学や社会学といった分野で複雑な因果関係を分析する際に非常に強力なツールとなる。しかし、アンケート調査などで収集されるデータには、回答者の個人的な解釈の違いや測定尺度の不完全性から生じる「測定誤差」がつき... -

媒介効果と調整効果:2つの「影響」を理解する
研究論文やデータ分析でよく耳にする「媒介効果」と「調整効果」。どちらも変数間の関係性を深く掘り下げる際に重要な概念であるが、その意味するところは大きく異なる。本記事では、これら二つの効果の違いを明確にし、具体的な例とRでの計算例を交えなが... -

媒介因子、媒介変数、媒介分析を徹底解説! データ分析の奥深さを知る
データ分析を進める上で、「ある原因が結果にどう影響するか」を直接的に見るだけでなく、その間に存在する「別の要因」の存在を意識することは非常に重要だ。この「別の要因」が、ときに原因と結果の関係性をより深く理解するための鍵となる。今回は、こ... -

媒介因子とは?研究デザインにおける重要な概念を徹底解説
疫学研究や社会科学研究において、ある事象が別の事象に影響を与えるメカニズムを解明することは非常に重要である。しかし、単に「AがBを引き起こす」というだけでなく、その間に別の要因が介在することがよくある。このような時に登場するのが「媒介因子... -

Rで実践!構造方程式モデリング:複雑な関係性を解き明かす強力なツール
構造方程式モデリング(SEM)は、社会科学、心理学、マーケティングなど、多岐にわたる分野で活用されている統計分析手法である。観測されたデータから、直接観測できない潜在的な変数間の因果関係や複雑なパスを統計的に推定・検定することが可能である。... -

欠測値の対処法:研究と分析を成功させるためのロードマップ
研究やデータ分析において、欠測値 (Missing Values) は避けて通れない問題である。データの一部が欠けていると、分析結果の信頼性が損なわれたり、偏った結論が導き出されたりする可能性がある。しかし、適切な対処法を知っていれば、この課題を克服し、... -

Full Information Maximum Likelihood (FIML) による欠損データ処理:概要とRでの実践
データ分析を行う際、欠損データは避けて通れない課題の一つである。単純な欠損処理方法では情報が失われたり、結果に偏りが生じたりする可能性がある。そこで注目されるのが、Full Information Maximum Likelihood(FIML)である。FIMLは、欠損データを統... -

欠測率の計算方法と論文への記載方法:研究の信頼性を高めるために
研究データには、しばしば「欠測値(Missing Values)」という問題がつきまとう。この欠測値を適切に処理することは、研究結果の信頼性や妥当性を確保するために不可欠である。本記事では、欠測率の基本的な計算方法から、統計解析ソフトウェアRを用いた具...
12