ロジスティック回帰の結果で出力される、Analysis of Deviance(EZR)、モデル係数のオムニバス検定(SPSS)、モデル全体の検定(JMP)とは何か?
一言で言えば、モデルの統計学的有意性の検定である。
ロジスティック回帰におけるDevianceとは何か?
Deviance(デビアンス)とは、対数尤度にー2をかけたものである。
対数尤度が大きいことは、データのモデルへの当てはまりが良いことを意味する。
対数尤度にー2がかかったデビアンスが大きいことは、データのモデルへの当てはまりの悪さを意味する。
対数尤度は尤度の対数である。
では尤度とは何か。
ロジスティック回帰における尤度 L は、モデルから計算されるエンドポイントありの予測確率 $ \hat{p} $ となしの予測確率 $ \hat{q} $ を全部掛け合わせたものである。
下記の式は添え字を省略している簡略版である。
$$ L = \prod \hat{p} \prod \hat{q} $$
ここで、$ \prod $ は、掛け合わせるという記号である。
この尤度の対数をとると、ロジスティック回帰における対数尤度になる。
掛け合わせの記号 $ \prod $ は、対数の世界では、足し合わせの記号 $ \sum $ に変わり、足し算に変わる。
$$ \log{L} = \sum \log \hat{p} + \sum \log \hat{q} $$
この対数尤度のー2倍が小さいほうが当てはまりが良いという指標になる。
ロジスティック回帰における Analysis of Deviance とは何か?
検討しようとしている説明変数が投入されているモデルのデビアンスと、何かを比べて、よしあしを判定するのが Analysis of Devianceである。
何と比べるのかと言うと、説明変数が一つも投入されていないモデルである。
なので、説明変数が完全にランダムで、まったく何も説明しない意味のない変数でない限り、必ず意味があるという結果が返ってくる。
すなわち、統計学的有意になる。
Analysis of Devianceが統計学的有意でない場合は、その説明変数によるモデルは統計学的には意味があるとは言えない。
EZRにおけるAnalysis of Devianceの出力
性別、年齢、体重でエンドポイントを説明するモデルを考えたとして、以下のように何も説明変数が投入されていないModel2と比較したときに、p値は0.0004597で、有意水準5%とすると、統計学的有意である。
つまり、このモデルは統計学的に意味があると言える。

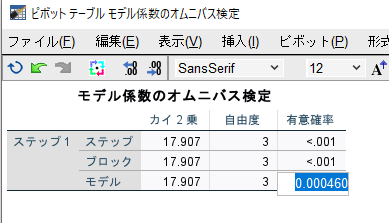
SPSSにおけるAnalysis of Deviance → モデル係数のオムニバス検定
SPSSの場合は、モデル係数のオムニバス検定とタイトルがついている表の「モデル」という行を見る。
その結果が統計学的有意かどうかで、モデルの有意性が判定できる。
JMPにおけるAnalysis of Deviance → モデル全体の検定
JMPの場合は、モデル全体の検定のp値を見て、判断する。
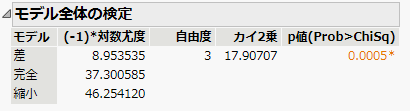
ちなみに、JMPは対数尤度がー2倍されておらず、ー1倍であるので、EZRと比べるとModel1(JMPでは完全)とModel2(JMPでは縮小)ともに半分の値になっている。JMPはそのような仕様である。
| 統計ソフト | モデル | -2 x or -1 x 対数尤度 |
|---|---|---|
| EZR | Model 1 | 74.601 |
| JMP | 完全 | 37.301 |
| EZR | Model 2 | 92.508 |
| JMP | 縮小 | 46.254 |
最終的なカイ2乗(デビアンス)は絶対値で同一である(17.907 = 92.508 – 74.601)。
まとめ
ロジスティック回帰におけるAnalysis of Devianceについて解説した。
モデルの有意性を判断する検定である。
SPSSでは、モデル係数のオムニバス検定と呼ばれている。
JMPでは、モデル全体の検定と呼ばれている。
参考になれば。
参考書籍
SPSSによる応用多変量解析
おすすめ書籍
EZR公式マニュアル









コメント