統計分析は奥深く、時には結果の信頼性に疑問を抱くこともある。特に、心理学や社会科学の分野で広く用いられる因子分析は、その性質上、サンプルの変動に影響を受けやすいという側面を持つ。しかし、もしその影響を最小限に抑え、より安定した、信頼性の高い因子構造を導き出す方法があるとしたらどうだろうか? 本記事では、その強力なツールである「ブートストラップ因子分析」に焦点を当て、その概要から具体的な使い方、Rを用いた計算例までを分かりやすく解説する。
ブートストラップ因子分析の概要
ブートストラップ因子分析は、統計的推論手法の一つであるブートストラップ法を因子分析に応用したものである。通常の因子分析が単一のサンプルデータに基づいて因子構造を推定するのに対し、ブートストラップ因子分析では、元のデータから繰り返し(通常は数千回)再標本化(リサンプリング)を行い、それぞれの再標本データに対して因子分析を実行する。
この繰り返し分析によって得られる多数の因子構造の結果を統合することで、以下の利点が得られる。
- 因子構造の安定性評価: 各再標本データから得られる因子負荷量や固有値のばらつきを見ることで、推定された因子構造がどの程度安定しているかを評価できる。
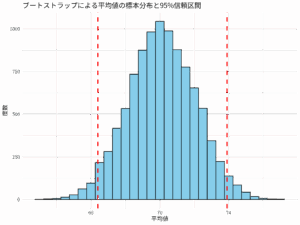
- 信頼区間の推定: 因子負荷量や固有値など、各パラメータの信頼区間を推定することが可能である。これにより、推定値の不確実性を定量的に示すことができる。
- サンプル変動へのロバスト性: 特定のサンプルに過度に依存することなく、より普遍的な因子構造を導き出すことができる。特に、サンプルサイズが小さい場合や、データに外れ値が含まれる場合に有効である。
ブートストラップ因子分析の使い所
ブートストラップ因子分析は、以下の状況で特にその威力を発揮する。
- 因子構造の頑健性を確認したい場合: 従来の因子分析で得られた因子構造が、他のサンプルでも同様に再現されるかを確認したい時。
- 小規模なサンプルで因子分析を行う場合: サンプルサイズが小さいと、因子分析の結果が不安定になりがちである。ブートストラップ因子分析は、このような場合に推定の信頼性を高めるのに役立つ。
- 因子負荷量や共通性などの信頼区間を推定したい場合: 推定された因子負荷量や共通性がどの程度の範囲で変動しうるのか、その不確実性を定量的に示したい時。
- 研究の再現性を高めたい場合: 分析結果が特定のデータセットに依存しないことを示し、研究の信頼性と再現性を向上させたい時。
具体例と R の計算例
ここでは、架空の心理尺度データを用いて、Rでブートストラップ因子分析を実行する例を示す。
シナリオ: ある心理学者が、5つの項目からなる「ストレス尺度」を作成し、因子分析を用いてその潜在的な構造を明らかにしようとしている。
Rでの計算例:
ブートストラップ因子分析にはpsychパッケージが便利である。
# パッケージのインストール(初回のみ)
# install.packages("psych")
# install.packages("boot") # ブートストラップ全般に使えるパッケージ
# パッケージの読み込み
library(psych)
library(boot)
# 架空のデータ作成
set.seed(123) # 再現性のためのシード設定
data <- data.frame(
item1 = round(rnorm(100, 30, 10)),
item2 = round(rnorm(100, 32, 9)),
item3 = round(rnorm(100, 28, 11)),
item4 = round(rnorm(100, 40, 12)),
item5 = round(rnorm(100, 38, 10))
)
# 因子分析を行う関数を定義
fa_func <- function(data, indices) {
d <- data[indices, ]
# 因子数を仮に2とする(スクリープロット等で事前に決定するのが望ましい)
fit <- fa(d, nfactors = 2, rotate = "varimax", fm = "minres")
# 因子負荷量を行ベクトルとして返す
return(as.vector(fit$loadings))
}
# ブートストラップの実行
# Rのboot::boot関数を使用
# R=1000はブートストラップの繰り返し回数
# 実際の分析では、2000回以上が推奨される。
boot_results <- boot(data = data, statistic = fa_func, R = 1000)
# ブートストラップ結果の確認(一部のみ表示)
print(boot_results)
# 因子負荷量の信頼区間を計算する例(項目1の第1因子負荷量)
# boot.ci関数で信頼区間を計算
# type="perc"はパーセンタイル法
boot.ci(boot_results, index = 1, type = "perc") # indexは因子負荷量のベクトル内の位置
# すべての因子負荷量の信頼区間を計算
# 5項目 × 2因子 = 10個の因子負荷量
cat("\n=== すべての因子負荷量の95%信頼区間 ===\n")
for (i in 1:10) {
ci_result <- boot.ci(boot_results, index = i, type = "perc")
cat(sprintf(
"因子負荷量 %d: (%.4f, %.4f)\n",
i, ci_result$percent[4], ci_result$percent[5]
))
}コードの説明:
- データ作成: 5つの項目からなる架空のデータセットを作成する。
fa_func関数の定義:boot関数に渡すための関数である。この関数は、ブートストラップによって選択されたデータ(d)に対して因子分析を実行し、その結果として得られる因子負荷量をベクトル形式で返す。nfactorsで因子数を指定するが、これは事前に他の方法(例:スクリープロット、平行分析)で決定しておくことが一般的である。rotateは因子回転法、fmは因子抽出法である。boot関数の実行:data: ブートストラップを行う元のデータ。statistic: 上で定義したfa_func。R: リサンプリングの回数。
boot.ci関数の実行:boot関数の結果から、特定のパラメータ(この場合は項目1の第1因子負荷量)の信頼区間を計算する。indexはfa_funcが返したベクトルの中での位置を示す。
実行結果:
> # すべての因子負荷量の信頼区間を計算
> # 5項目 × 2因子 = 10個の因子負荷量
> cat("\n=== すべての因子負荷量の95%信頼区間 ===\n")
=== すべての因子負荷量の95%信頼区間 ===
> for (i in 1:10) {
+ ci_result <- boot.ci(boot_results, index = i, type = "perc")
+ cat(sprintf(
+ "因子負荷量 %d: (%.4f, %.4f)\n",
+ i, ci_result$percent[4], ci_result$percent[5]
+ ))
+ }
因子負荷量 1: (-0.5242, 0.9987)
因子負荷量 2: (-0.3203, 0.9969)
因子負荷量 3: (-0.3746, 0.9980)
因子負荷量 4: (-0.2605, 0.9969)
因子負荷量 5: (-0.5194, 0.9993)
因子負荷量 6: (-0.5959, 0.9798)
因子負荷量 7: (-0.3917, 0.9954)
因子負荷量 8: (-0.3917, 0.9952)
因子負荷量 9: (-0.3565, 0.9733)
因子負荷量 10: (-0.5540, 0.9822)結果解釈
ブートストラップ因子分析の結果は、主に以下の点に注目して解釈する。
- 因子負荷量の信頼区間:
boot.ci関数を用いて計算される信頼区間は、真の因子負荷量がこの区間内に存在する確率が高いことを示す。例えば因子負荷量1(第一因子の質問1の因子負荷量)の 95%信頼区間が$[-0.5242, 0.9987]$であれば、真の負荷量がこの範囲にあると95%の確信度で言えるわけである。信頼区間がゼロを含まない場合、その因子負荷量は統計的に有意であると判断できる。 - 因子の構造: 繰り返し得られた因子構造全体を見て、特定の因子に安定して負荷する項目群があるか、因子間の分離が明確かなどを評価する。もし、ブートストラップサンプル間で因子構造が大きく変動するようであれば、元の因子構造の解釈には慎重になる必要がある。
まとめ
ブートストラップ因子分析は、単一のサンプル分析では見過ごされがちな、因子構造の安定性や推定値の不確実性を明らかにするための強力なツールである。特に、サンプルサイズが限られている場合や、よりロバストで信頼性の高い因子構造を求めたい場合に、その真価を発揮する。本記事で紹介したRの計算例を参考に、ぜひ自身の研究や分析に応用し、より深い洞察を得るための一助としていただければ幸いである。





コメント