ブートストラップとは、小さいサンプルを復元抽出で何度もサンプリングして、疑似的に何度も試行したことにして、その結果から推定値の直接的な95%の範囲を求めたりする方法。
ブートストラップを使ったロジスティック回帰分析の方法をご紹介。
ブートストラップとは?
ブートストラップとは、小さいサンプルを復元抽出で何度もサンプリングして、疑似的に何度も試行したことにして、その結果から推定値の直接的な95%の範囲を求めたりする方法。
復元抽出とは、たまたま複数回同じデータがとられてもOKとする方法。
オリジナルのサンプルとサイズ(データの数)が同じサンプルをたくさん作る。
このほうが現実世界に近い。
こうすると、データの構成がばらつく。
オリジナルのデータから、似たようなサンプルをたくさん作って、小さいサイズのオリジナルデータでも信頼性高い、区間推定を行える方法だ。
ちなみに、ブートストラップは靴紐(ブーツのひもかな?)という意味で、アメリカのことわざで、湖に散歩に行って溺れた人が、自分の靴紐につかまって生還するというものがあり、そこから、困ったことがあっても自力で何とかするという意味だそうである。
そこから、小さいサイズのサンプルでも、そのサンプルだけで、自力で何とかするという意味で、ブートストラップ法という名前がついたのだとか。
新谷先生が、発明者のEfron先生から直々に聞いたとのことで、間違いないようだ。
24秒あたりから説明あり。
ググってみたところ、こんなブログ記事があった。
https://ameblo.jp/sexyrockingenglish/entry-10567716502.html
ブートストラップとは、ブーツのかかとについている、小さなループの部分のことを言っているみたい。
”ブートストラップ”というのは、ブーツのかかとの部分についている、小さなループの部分だ。 昔、18世紀のドイツの貴族、ミュンヒハウゼン男爵が底なし沼に落ちたが、自分の履いていたブーツの小さなブートストラップを引っぱりあげて、自力で脱出したというところから、
“Pulling himself up by his own bootstraps.”
は、”自分の力でなんとかする、小さな始まりから大きな成功をつかむ”という意味のことわざになった。(でもこれはただのお話で、本当の話ではないとされている。)
ブートストラップ ロジスティック回帰スクリプト
以下のWebサイトでブートストラップスクリプトを公開してくれていたので、こちらを参考にした。
Bootstrap with logistic regression | R-bloggers
まずlibrary(boot)で、boot パッケージを呼び出す。
Stop400が目的変数、Age, Sex, WBC45000の3つの変数を説明変数にしたロジスティック回帰を考える。
fit <- のところをご自分のモデルに置き換えればOK。
library(boot)
logit_test <- function (d,indices) {
d <- d[indices,]
fit <- glm(Stop400 ~ Age + Sex + WBC45000,
family=binomial(logit), data=d)
return(coef(fit))
}
dは使うデータセット名、indicesは、データの行で、一部を使うなら、その部分を指定することができる。
logit_test(d=Imatinib_Stop, indices=1:100)
ブートストラップする
以下のスクリプトが実際にブートストラップするスクリプトだ。
dataでデータセットを、statisticで上記で設定したロジスティックモデルを指定する。
Rはブートストラップサンプリングの数で、1e4は $ 1 \times 10^4 = 10000 $ セットの意味である。
紹介してくれているWebサイトのオリジナルでは1e5で、10万セットになっていた。
boot_fit <- boot(
data = Imatinib_Stop,
statistic = logit_test,
R = 1e4
)
boot_fit
出力結果は以下のとおりである。
boot_fitの結果の、originalというところが、ブートストラップ前の単にロジスティック回帰分析をしたときのパラメータの推定値である。
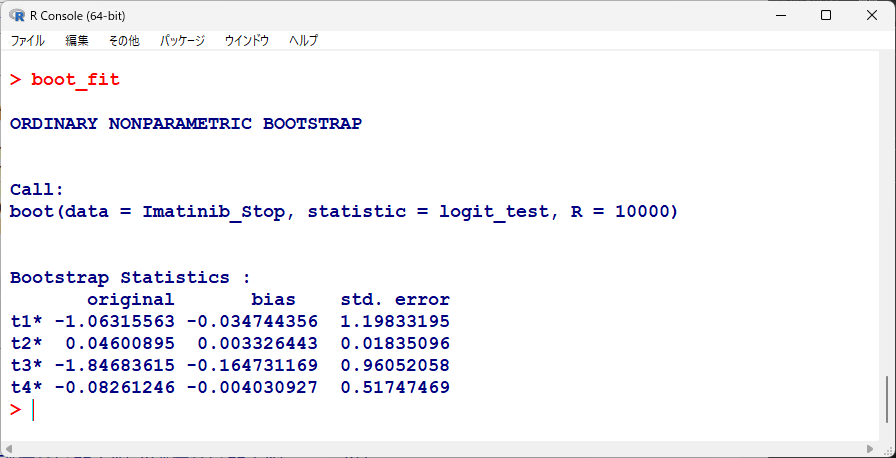
biasは、originalとブートストラップ平均値との差を示している。
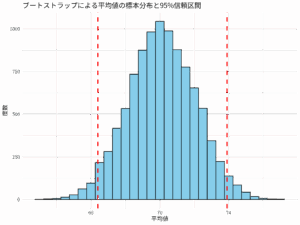
ブートストラップで得た 10,000 データの平均をとってみると、以下のようになる。
t1~t4の結果に相当する。
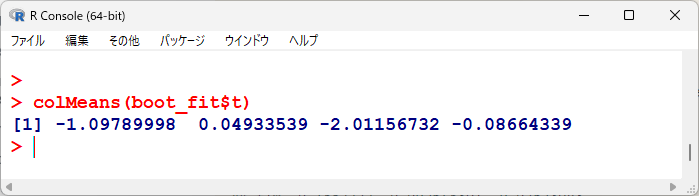
originalとの差をとると、biasの値に一致する。
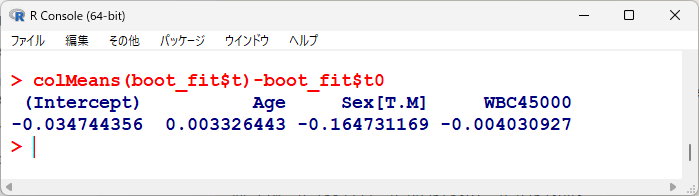
つまりは、ブートストラップをすることで、いくらかのバイアスは生じるということである。
ブートストラップ95%信頼区間を出力する
1万回ブートストラップ ロジスティック回帰分析を行った結果から、偏回帰係数の95%信頼区間を出力してみる。
パラメータとしては、切片と、Age, Sex, WBC45000の3つの合計4つが得られる。
tとあるのがパラメータのブートストラップで得られた値で、切片、Age, Sex, WBC45000の順に1~4行目となっている。
Rは10000回のブートストラップを意味している。
boot.conf.int <- function(m, R){
dat0 <- data.frame()
dat1 <- data.frame()
for (i in 1:m){
ll <- sort(boot_fit$t[,i])[R*0.025]
ul <- sort(boot_fit$t[,i])[R*0.975]
name <- paste("t",i,sep="")
dat0 <- data.frame(name, ll, ul)
dat1 <- rbind(dat1, dat0)
}
print(dat1)
}
boot.conf.int(m=4, R=10000)
出力結果は以下のとおりである。
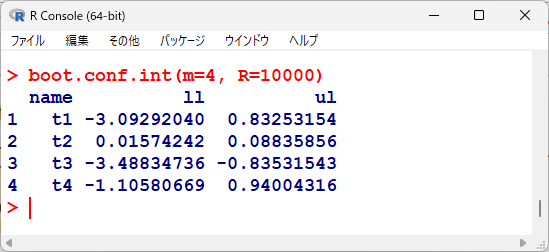
95%範囲が、llとulで表現されている。
ゼロをまたがない、t2(Age)とt3(Sex)が、統計学的有意と判断できる。
結局のところ、ブートストラップをする前の単純にロジスティック回帰分析を行った時の95%信頼区間も同様の結果であったので、顕著な違いはなかったと言える。
EZRのロジスティック回帰分析のRスクリプトを少し修正して exp() する前の対数で表現すると以下のようになる。

X1が点推定値、X2が95%信頼区間下限値、X3が95%信頼区間上限値。
この数値と似た数値がブートストラップでも得られたということである。
ただし、ブートストラップをすることで、疑似的ではあるものの、多数回の結果をもとにより再現性が高い結果が得られたと言えるかもしれない。
まとめ
小さいサイズのサンプルの時に、復元抽出を多数回行うことで、疑似的な繰り返し試行を行い、信頼性の高い解析結果を提供してくれるブートストラップ手法をロジスティック回帰分析に適用してみた。
サンプルサイズが小さい場合に、この手法を付け加えることで、小サンプルサイズの欠点を補った解析結果が得られると言えるだろう。
参考になれば。
参考サイト
https://ameblo.jp/sexyrockingenglish/entry-10567716502.html
Bootstrap with logistic regression | R-bloggers
R Bootstrap Statistics & Confidence Intervals (CI) Tutorial | DataCamp
参考動画
おすすめ書籍
EZR公式マニュアル







コメント
コメント一覧 (3件)
[…] R でブートストラップ ロジスティック回帰分析を行う方法 […]
ブートストラップ法で質問になります。
同種造血幹細胞移植後の静脈血栓塞栓症VTE(PE・DVT)を予測するモデルを作成し、論文投稿を予定しています。VTEが1292例中28例しかおらず、コホートを分ける代わりに、ブートストラップ法で検証しました。しかし、ブートストラップ法で計算したC統計量が同じ数値しか出ませんでした。chatGPTに尋ねたところ、代わりに多変量モデルにするように薦められました。
質問1
ブートストラップ法で計算したC統計量が同じ数値しか出なかった理由はVTE発症数が少なすぎるからでしょうか。
質問2
「ブートストラップ法を多変量モデルにする」というのは統計的に妥当な方法でしょうか。
何卒ご指導よろしくお願い申し上げます。
ご質問ありがとうございます!お答えします。質問1は、そのとおりと思います。質問2は、妥当と思います。以上です!