手元にあるデータだけでは、本当に信頼できる統計的な結論は出せないのではないか?そう悩んだことはないだろうか。特に、データ数が少ない場合や、複雑な統計量に関心がある場合、その悩みは尽きないかもしれない。そんな時に非常に強力なツールとなるのがブートストラップ法だ。この記事では、ブートストラップ法の基本的な考え方から、具体的なRでの計算方法、さらには応用例まで、分かりやすく解説する。
ブートストラップ法の概要
ブートストラップ法は、手元にある限られた標本データから、あたかも多数の新しい標本を採取したかのように振る舞い、統計的推測を行うための強力なリサンプリング(再標本化)手法である。この手法の核心は、「復元抽出」というシンプルなアイデアにある。
具体的には、以下の手順を繰り返す。
- 元の標本から復元抽出で新しい標本を生成する:手元にあるN個のデータから、重複を許してN個のデータをランダムに選び出し、新しい「ブートストラップ標本」を作成する。元の標本と同じサイズにするのが一般的だ。
- 統計量を計算する:生成されたブートストラップ標本ごとに、推定したい統計量(例えば、平均値、中央値、分散、相関係数など)を計算する。
- 多数回繰り返す:このプロセスを数千回、あるいは数万回繰り返すことで、元の標本から得られる可能性のある統計量の分布(ブートストラップ分布)をシミュレートする。
このブートストラップ分布を利用することで、母集団に関する統計量の信頼区間の推定や、仮説検定などを行うことができる。
ブートストラップ法の使い所
ブートストラップ法は、様々な場面でその真価を発揮する。
- データ数が少ない場合:特に、解析に使えるデータが限られている場合、ブートストラップ法は統計的推測の信頼性を高める有効な手段となる。
- 複雑な統計量の場合:平均や分散のような単純な統計量だけでなく、中央値、分位数、相関係数、回帰係数など、理論的な分布が導きにくい複雑な統計量に対しても、その分布や信頼区間を推定することができる。
- 分布の仮定を置きたくない場合:パラメトリックな手法のように、データが特定の確率分布(例:正規分布)に従うという仮定を置かずに推測を行いたい場合に非常に有効だ。ブートストラップ法は、データの経験分布に基づいて推測を行うため、よりロバストな結果が得られる。
- 信頼区間の推定:推定量の信頼区間を、標準的な方法では計算が難しい場合でも、ブートストラップ分布から直接的に推定できる。
- バイアスの推定と補正:推定量のバイアス(偏り)を推定し、必要であれば補正するために利用することもある。
基礎的な具体例とRでの計算方法:平均値の信頼区間
ここでは、ブートストラップ法を使って、あるデータセットの平均値の95%信頼区間を推定する例を見てみよう。
シナリオ
ある学校の生徒15人の数学のテストの点数データがあるものとする。このデータから、全生徒の数学の平均点に関する95%信頼区間を推定したい。
Rでの計算方法
Rでは、bootパッケージがブートストラップ法を非常に簡単に行えるようにしてくれる。
まず、サンプルデータを作成する。
R スクリプト例:
# データを準備
set.seed(123) # 再現性のためにシードを設定
scores <- c(65, 70, 75, 80, 85, 60, 90, 72, 78, 88, 68, 73, 82, 77, 92)
次に、ブートストラップを行うための関数を定義する。この関数は、データとインデックスを受け取り、計算したい統計量(ここでは平均値)を返す。
# 平均値を計算する関数
mean_function <- function(data, indices) {
mean(data[indices])
}
boot関数を使ってブートストラップを実行する。
# bootパッケージをロード
library(boot)
# ブートストラップを実行 (R = 10000回繰り返す)
boot_results_mean <- boot(data = scores, statistic = mean_function, R = 10000)
# 結果の表示
print(boot_results_mean)
ブートストラップの結果から信頼区間を計算する。
# 信頼区間の計算 (Percentile method)
boot.ci(boot_results_mean, type = "perc")
実行結果:
> # 信頼区間の計算 (Percentile method)
> boot.ci(boot_results_mean, type = "perc")
BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
Based on 10000 bootstrap replicates
CALL :
boot.ci(boot.out = boot_results_mean, type = "perc")
Intervals :
Level Percentile
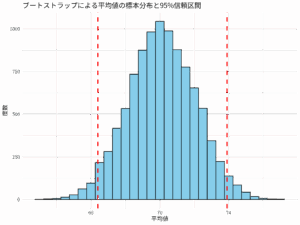
95% (72.47, 81.60 )
Calculations and Intervals on Original Scale
> この結果から、「数学の平均点の95%信頼区間は[72.47, 81.60]である」と言える。これは、もし同じプロセスを何度も繰り返したら、95%の確率で真の母平均がこの区間内に含まれることを意味する。
応用的な具体例とRでの計算方法:回帰係数の信頼区間
ブートストラップ法は、より複雑な統計モデリング、例えば線形回帰の回帰係数の信頼区間推定にも利用できる。
シナリオ
生徒の数学の点数が、学習時間(時間)で予測できるかどうかを調べたいとする。線形回帰モデルを構築し、学習時間の係数(傾き)の信頼区間をブートストラップ法で推定する。
Rでの計算方法
まず、サンプルデータを作成する。
R スクリプト例:
# データを準備
set.seed(456) # 再現性のためにシードを設定
learning_hours <- c(2, 3, 4, 5, 6, 1, 7, 3, 4, 6, 2, 3, 5, 4, 7)
scores_reg <- c(68, 72, 76, 80, 84, 62, 90, 70, 75, 86, 66, 71, 81, 78, 92)
data_reg <- data.frame(hours = learning_hours, score = scores_reg)
次に、ブートストラップを行うための関数を定義する。この関数は、データとインデックスを受け取り、線形回帰モデルをフィットし、学習時間の係数(ここではhoursの係数)を返す。
# 回帰係数を計算する関数
reg_coef_function <- function(data, indices) {
d <- data[indices, ] # ブートストラップ標本を作成
model <- lm(score ~ hours, data = d) # 線形回帰モデルをフィット
coef(model)["hours"] # hoursの係数を返す
}
boot関数を使ってブートストラップを実行する。
# bootパッケージをロード (すでにロード済みなら不要)
library(boot)
# ブートストラップを実行 (R = 10000回繰り返す)
boot_results_reg <- boot(data = data_reg, statistic = reg_coef_function, R = 10000)
# 結果の表示
print(boot_results_reg)
ブートストラップの結果から信頼区間を計算する。
# 信頼区間の計算 (Percentile method)
boot.ci(boot_results_reg, type = "perc")
実行結果:
> # 信頼区間の計算 (Percentile method)
> boot.ci(boot_results_reg, type = "perc")
BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
Based on 10000 bootstrap replicates
CALL :
boot.ci(boot.out = boot_results_reg, type = "perc")
Intervals :
Level Percentile
95% ( 4.415, 5.047 )
Calculations and Intervals on Original Scale
> この結果から、「学習時間の係数の95%信頼区間は[4.415, 5.047]である」と言える。これは、学習時間が1時間増えるごとに数学の点数が平均的に約 4.4 点から 5.0 点の間で増加するといった解釈が可能となる。
まとめ
ブートストラップ法は、手元にあるデータから、統計的な推測をよりロバストに行うための強力なツールだ。特に、データ数が少ない場合や、複雑な統計量、あるいは分布の仮定を置きたくない場合にその威力を発揮する。
Rのbootパッケージを使えば、基本的な平均値の信頼区間推定から、線形回帰の係数推定まで、様々な統計的推測にブートストラップ法を簡単に適用できる。
この手法を使いこなすことで、あなたのデータ分析はより信頼性が高く、説得力のあるものとなるだろう。ぜひ、自身のデータでブートストラップ法を試してみてほしい。





コメント