R で Box-Cox 変換を行う方法

連続量を何らかの方法で正規分布に近づける方法はいくつかある。

ここではBox-Cox変換の方法をまとめてみた。

R で Box-Cox変換を行う実例

まず、car パッケージを呼び出す。

library(car)

car パッケージの中の、powerTransform()とbcpower()を使って変換する。

例に使うのは、EZR公式マニュアルの付録でついてくるデータ ElderlyAML 内のLDHのデータである。

powerTransform()で、λ（ラムダ）というパラメータを推定する。

Box-Cox変換にはこのパラメータが必要になる。

ptf.LDH1 <- powerTransform(ElderlyAML$LDH)

λを確認してみると、 -0.3184011であった。

> ptf.LDH1$lambda
ElderlyAML$LDH
-0.3184011

次に、bcPower()を使って、先ほど計算した λを用いて、Box-Cox変換を行う。

bc.LDH1という新しい名前の変数にする。

bc.LDH1 <- bcPower(ElderlyAML$LDH, ptf.LDH1$lambda)

要約値を出してみても、よくわからない値になっている。

LDHは、通常、数百程度の値なので、全然想像がつかない。

> summary(bc.LDH1)
Min. 1st Qu.  Median    Mean 3rd Qu.    Max.    NA's 
  2.444   2.597   2.656   2.662   2.737   2.862       1

Box-Cox変換した値の分布を確認してみる

ヒストグラムでデータの分布を確認してみる。

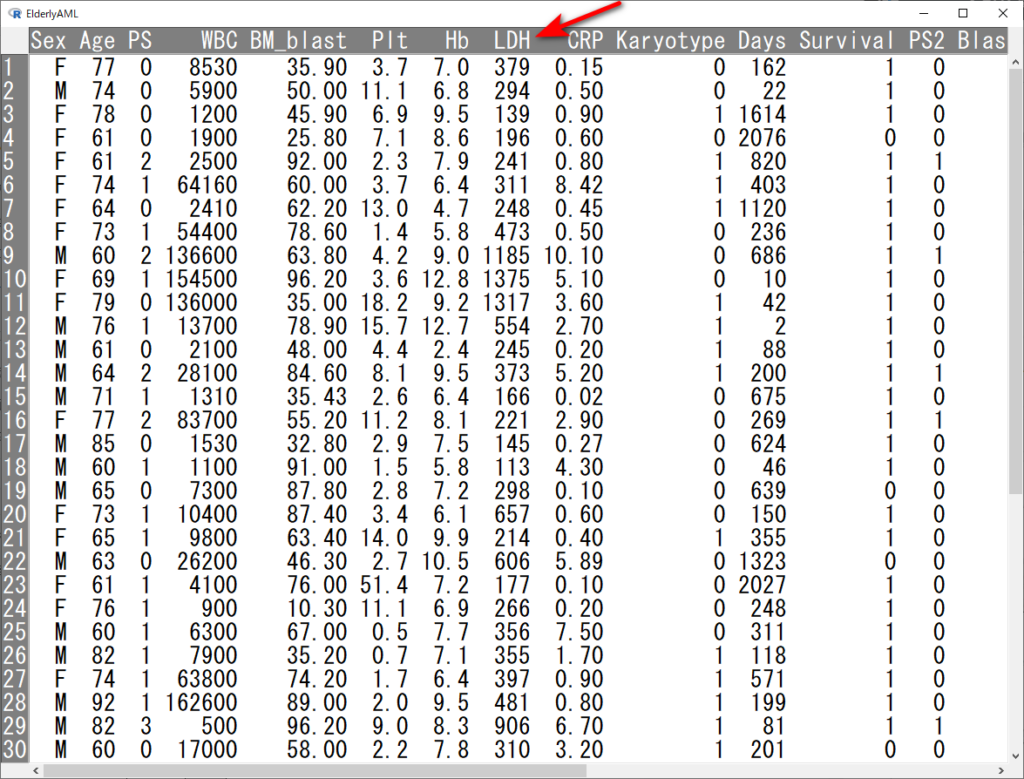
まず、元のデータをそのまま使ってヒストグラムを描いてみると、ものの見事に右に裾を引いている。

hist(ElderlyAML$LDH)

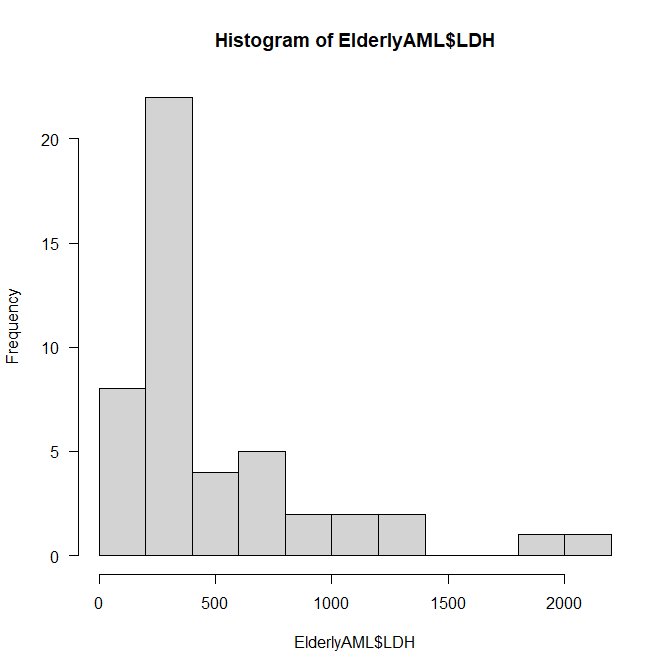
Box-Cox変換後の値を使うと、非常にきれいな左右対称の分布になっていることがわかる。

hist(bc.LDH1)

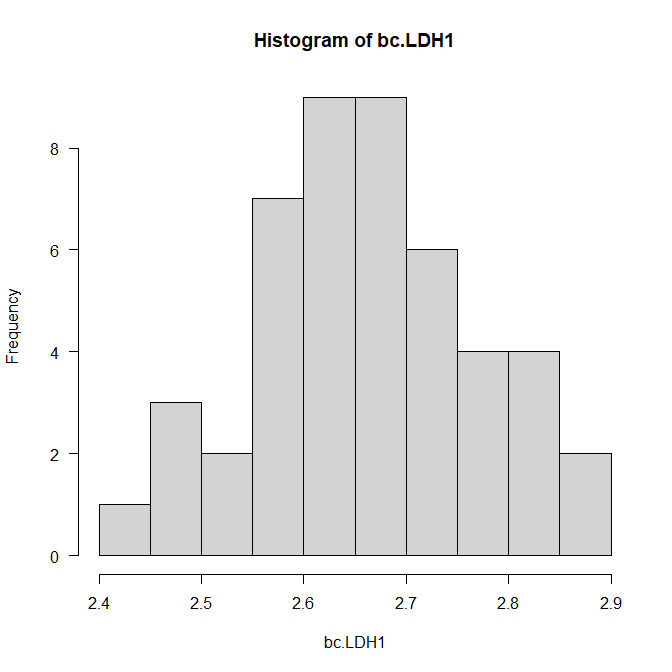
ちなみに、よく知られている自然対数変換の場合は、元のデータよりは左右対称になっているが、中央より少し低いところで、狭い範囲に集中しすぎているようなグラフになるため、Box-Cox変換のほうが優れているように思える。

hist(log(ElderlyAML$LDH))

Box-Cox変換した値を逆変換して元の世界に戻す方法

Box-Cox変換は、式で表すとλがゼロでない場合は以下のようになる。

$$ y(\lambda) = \frac{y^{\lambda} – 1}{\lambda} $$

なので、逆変換するならば、

$$ (y \times \lambda + 1)^{1/\lambda} $$

で計算できる。

先ほど変換した値 bc.LDH1 を元に戻すならば、以下のようにすると元に戻る。

Box-Cox変換した値を使って、回帰分析を行った後に、予測値を使うために、元に戻したい場合などに使う。

rev.LDH1 <- (bc.LDH1 * ptf.LDH1$lambda + 1)^(1/ptf.LDH1$lambda)

summary()をとってみると、完全に一致していて、元に戻ったことがわかる。

> summary(rev.LDH1)
Min. 1st Qu.  Median    Mean 3rd Qu.    Max.    NA's 
  113.0   246.5   355.0   518.9   629.5  2007.0       1 
> summary(ElderlyAML$LDH)
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max.    NA's
113.0   246.5   355.0   518.9   629.5  2007.0       1

まとめ

正規分布していない連続量を正規分布に近づける方法として、Box-Cox変換がある。

自然対数変換でうまくいかないときの奥の手として知っておくと、助かることがあるかもしれない。

参考になれば。

参考ウェブサイト

Box-cox変換を用いて正規分布に従わないデータを解析をしてみよう！｜スタビジ

おすすめ書籍

EZR公式マニュアル