回帰分析・線形回帰・重回帰– category –
-

線形回帰の罠:なぜ「データの正規性」は必須ではないのか
統計学やデータ分析の初学者が線形回帰を学ぶ際、最初につまずくポイントがある。それが「正規性の仮定」だ。「分析対象のデータ(目的変数)が正規分布していなければ、回帰分析は使えない」と思い込み、分析を断念したり、無理なデータ変換を繰り返した... -

重回帰分析における重み付き最小二乗法:データの潜在的な声を聴く
重回帰分析は、複数の説明変数を用いて目的変数を予測する強力な統計手法である。しかし、OLS(Ordinary Least Squares:通常の最小二乗法)を適用する際に、ある重要な仮定が満たされない場合、そのモデルの信頼性が損なわれることがある。それが「等分散... -

Rで回帰直線の検定と信頼区間:lm関数を使わずに計算する
単回帰分析では、目的変数と説明変数の間に直線的な関係があるかを調べる。Rのlm関数を使えば簡単に分析できるが、その裏側にある計算ロジックを理解することも重要だ。この記事では、lm関数に頼らずに回帰直線の主要な要素、つまり回帰係数の推定、その検... -

回帰分析の奥深さ:$t$ 値の2乗と$F$ 値が等しい理由を解き明かす!
回帰分析は、変数間の関係性を明らかにする強力な統計ツールだ。その結果を解釈する際、$t$ 値や $F$ 値といった統計量を目にすることが多いだろう。特に、単回帰分析においては、回帰係数の $t$ 値の2乗が、回帰モデル全体の有意性を検定する $F$ 値と常... -

重回帰分析の結果の書き方 ― 論文にはどの数値を書いたらよいか
教科書的には何を計算するかは決まっているが、論文にどの数値を掲載するかは決まっていない。 そういうときは、実例をもとに、まねするのが良いが、最低限の目安を示す。 回帰分析の結果の書き方の基本 一番大事な要素は、点推定値と95%信頼区間である。... -

EZR で多重代入法を行う方法
EZR で多重代入法を行いたい場合、どのようにしたらよいか EZR には、多重代入のメニューはないが、R スクリプト枠にスクリプトを書いていく方法で実行できる はじめに 欠損値(欠測値と同じ)があるデータセットにおいて、推定値にバイアスがかかると言わ... -

重回帰分析における当てはまりの良さに関するいくつかの指標の違いと使い分け
重回帰分析(以下、線形回帰も同義)には当てはまりの良さの指標としていくつかあるが、それらの違いと使い分けはどうしたらよいのか? 自由度調整済み決定係数の特徴 説明率とも言われる決定係数の説明変数の個数を考慮したバージョン 0 から 1 の間の値... -

決定係数が小さい場合の考え方
重回帰分析の評価指標の一つ、決定係数が小さいときに、どう考えたらよいか どのくらいの数値であったら、大丈夫なのだろうか 決定係数がどのくらいであれば意味があるか? 決定係数は、0.7 以上欲しいとか、0.5 でもよいとか、分野によっては 0.3 でもよ... -

標準化偏回帰係数の簡単な解説
標準化偏回帰係数(ひょうじゅんかへんかいきけいすう)とは何か? 一言で言えば、単位が異なる説明変数の、目的変数に対する影響力を比較したいときに、便利な数値と言える 順を追って、式なしでイメージだけでわかりやすく解説 標準化偏回帰係数の前に回... -

SPSS を使ってやりたい解析別重回帰分析の実行方法
SPSS で重回帰分析をしたい場合、どのようにすればよいか やりたいこと別にまとめてみた 説明変数が連続データの場合で、交絡因子調整が目的の場合 目的変数、説明変数ともに連続データで、交絡因子調整が目的の場合は、以下のように解析する 分析 → 回帰 ... -

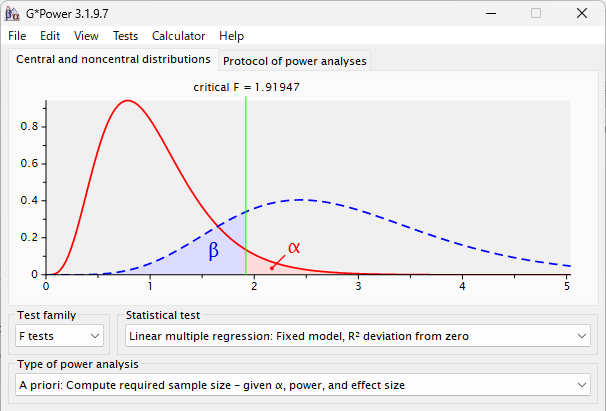
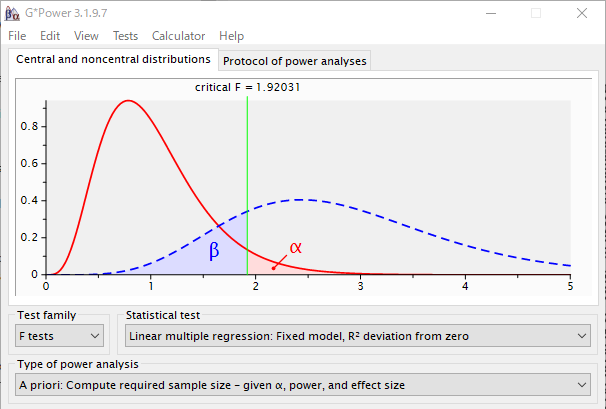
G*Power で重回帰分析に必要なサンプル数を計算する方法
G*Power は、サンプルサイズや検出力を計算するソフトウェアである 重回帰分析のサンプルサイズや検出力を計算する方法の紹介 GPower で重回帰分析のサンプル数を計算する方法 重回帰分析のサンプル数を計算するときは、予想される決定係数を見積もる必要... -

R で IPTW 重回帰で行ってロバスト分散を用いた信頼区間を求める方法
IPTW 重回帰を実施した後、ロバスト分散から信頼区間を求める方法 ロバスト分散信頼区間を求める必要性 IPTW(逆確率重み付け)の元となる傾向スコアの値は、真の値ではなく、推定値であるため、通常の重み付き回帰のソフトウェアが出力する分散の推定量は... -

重回帰分析の説明変数に対数変換した変数がある場合の結果の書き方
説明変数を対数変換した場合の重回帰分析の結果の書き方 重回帰分析の結果の書き方 重回帰分析をはじめ、様々な回帰分析の結果の書き方を見比べられる、リンク集はこちら 重回帰分析の結果の書き方 対数変換した説明変数がある場合どう書くか 例 1 : ( lo... -

SPSS でダミー変数を作成し重回帰分析でカテゴリ変数を使う方法
重回帰分析で、独立変数にカテゴリ変数を使う方法を解説する。 SPSSでは、ダミー変数を作成しておく必要がある。 ダミー変数とは何か? ダミー変数の作り方は? 重回帰分析をSPSSで行う方法 重回帰分析をSPSSで行う場合、2つの方法がある。 ひとつは、「... -

SPSS で交互作用項を作って交互作用項を含む重回帰分析を行う方法
重回帰分析に交互作用を含んだ解析をSPSSで計算する方法。 SPSSの重回帰分析では、交互作用項を自動で作ってくれない。 どのように作って、どのように解析すればよいか? SPSSで交互作用項の作り方 重回帰モデル内で交互作用の検討をするためには、交互作... -

重回帰分析の計算方法
重回帰分析は偏回帰係数を求めて予測式(回帰式)を作り、標準化偏回帰係数の計算、回帰式の有意性の分散分析、決定係数の算出、偏回帰係数の検定、など行うが、実際どんな計算をしているのか? 実際どんな計算をしているかわかると、偏回帰係数や標準化偏... -

回帰分析における 7 つの仮定
目的変数が正規分布している必要はない。 説明変数も正規分布している必要はない。 前提知識 実際に測定された目的変数を実測値と言う。 回帰式で計算された目的変数を予測値と言う。 実測値と予測値の差を残差と言う。 正式には母集団の誤差項の話になる... -

SPSS と GPower で重回帰分析に必要なサンプル数を計算する方法
重回帰分析を実施するのにサンプル数はどのくらい必要か? ここでいうサンプル数とは、サンプルサイズのこと。 重回帰分析のサンプルサイズはどのように計算するのか? 重回帰分析の効果量とは何か? 重回帰分析のサンプル数計算に必要な値は? サンプル数... -

決定係数とモデルの有意性の分散分析 ― 重回帰モデルの評価としての意義
重回帰モデルの評価指標の決定係数とモデルの有意性の分散分析の検定はどのように使い分ければよいのか? 決定係数とは? 決定係数とは、推定された重回帰モデルが実際のデータにどの程度当てはまっているかを表す指標である。 0から1の範囲の数値をとり... -

直交対比の簡単な説明
直交対比とは何か? 直交対比の直交とは? 直交とは何か? 英語では、orthogonal と言う。 Orthogonal とは何か? https://www.collinsdictionary.com/dictionary/english/orthogonal Web辞書で確認すると、直角とか直交という意味が1番基本となる意味であ... -

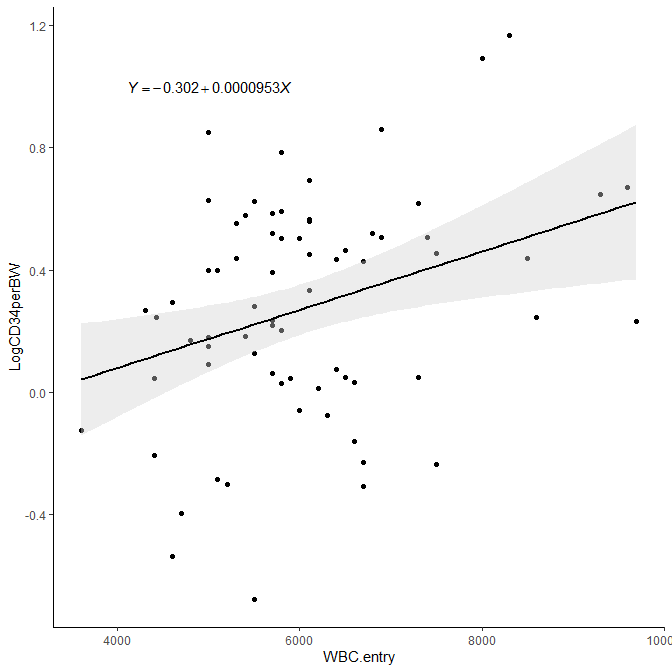
R の ggplot で書いた回帰直線に geom_smooth で 95 % 信頼区間を付ける方法
EZRで ggplot2 を使って95%信頼区間と回帰式付き回帰直線を描く方法。 EZRで回帰直線に95%信頼区間を描きたい場合どうするか? ggplot2 を使うと簡単・きれいに描ける。 ggplot で回帰直線を書く方法 ggplot2 とは? ggplot2 とは、簡単にきれいなグラフが... -

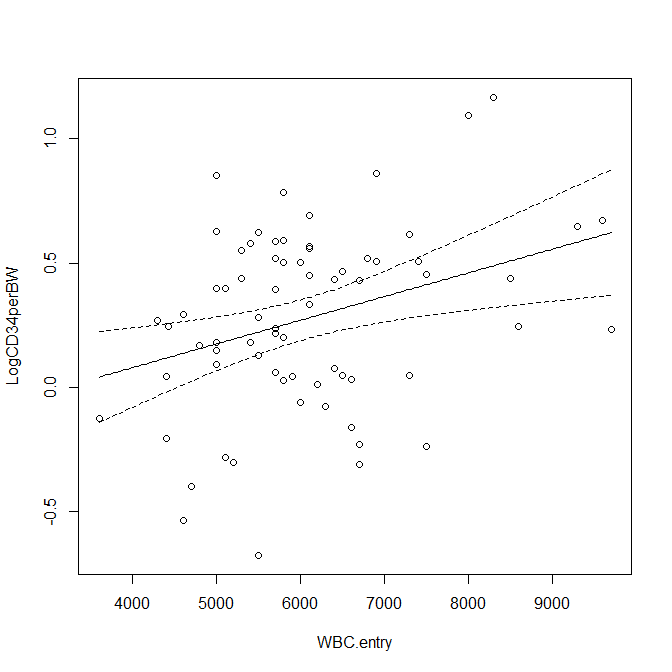
EZR で書いた回帰直線に信頼区間を付ける方法
EZRで回帰直線のグラフに95%信頼区間を付ける方法 回帰直線を書くために EZRで線形回帰(単回帰)を実行する まずEZRで単回帰を実行する。 例えば、以下のような感じに R スクリプト窓に出力される。 #####線形回帰(単回帰、重回帰)##### library(aod, pos... -

逆確率重み付け IPTW の説明と EZR で逆確率重み付け回帰を行う方法
逆確率重み付けとは、傾向スコアの逆数を用いて、人数があまり多くない層を厚くする方法で、処方の有無の背景をそろえる方法である。 重回帰で用いる方法。 逆確率重み付けとは? 逆確率重み付けは、Inverse Probability of Treatment Weighting が英語の... -

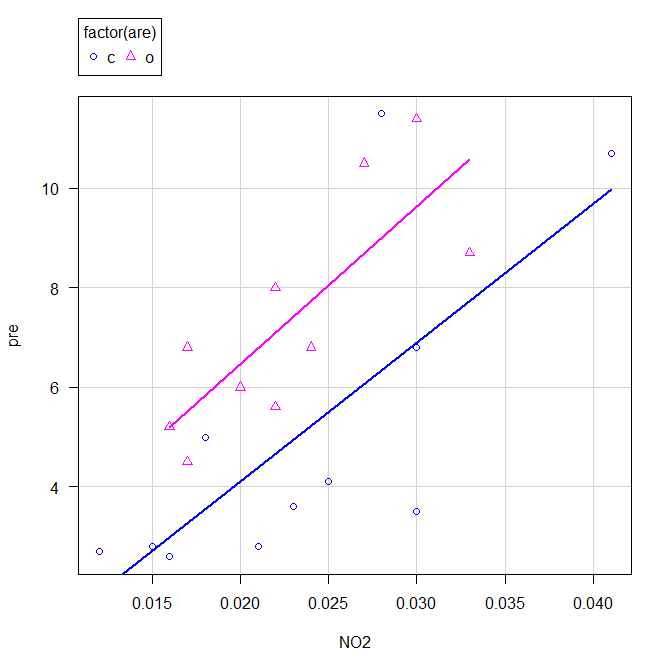
EZR で共分散分析を行い回帰直線を比較する方法
共分散分析を使えば、2つの回帰直線の傾きや切片が異なるかどうか検討できる。 直接的な傾きの差の検定や切片の差の検定ではないが、同様な結果が簡単に得られるので、共分散分析でよいと思っている。 データの準備 こちらを題材として、EZRで再解析してみ... -

線形回帰モデルの種類と簡単な解説
線形回帰の種類をわかりやすく解説。 線形回帰とは? 線形回帰の線形の由来は、線形結合からきている。 線形結合とは、以下のような式で表されることを意味している。 $$ \beta_1 X_1 + \beta_2 X_2 + \dots + \beta_n X_n $$ ここで β は (偏) 回帰係数の... -

傾向スコアマッチング回帰分析 簡単な説明
傾向スコアマッチングは、ある因子についてランダム化していなかった観察研究データにおいて、そのある因子以外は同様にした2つのグループをマッチングで作成する方法である。 目的変数が連続量の場合でも利用可能だろうか? 傾向スコアマッチングとは? ... -

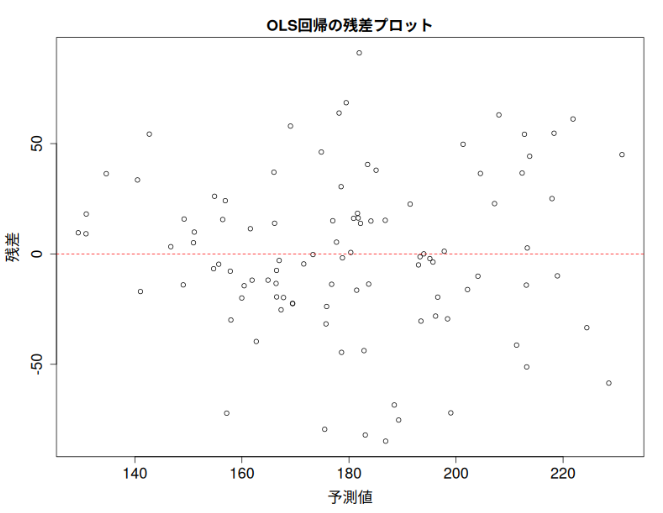
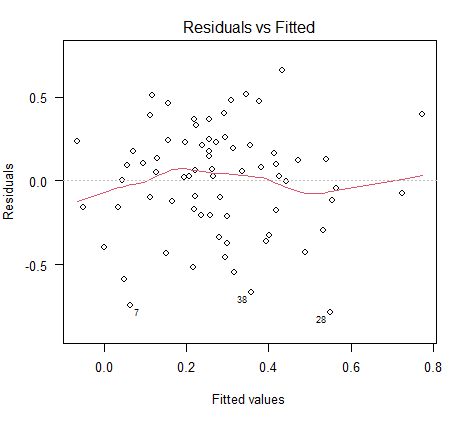
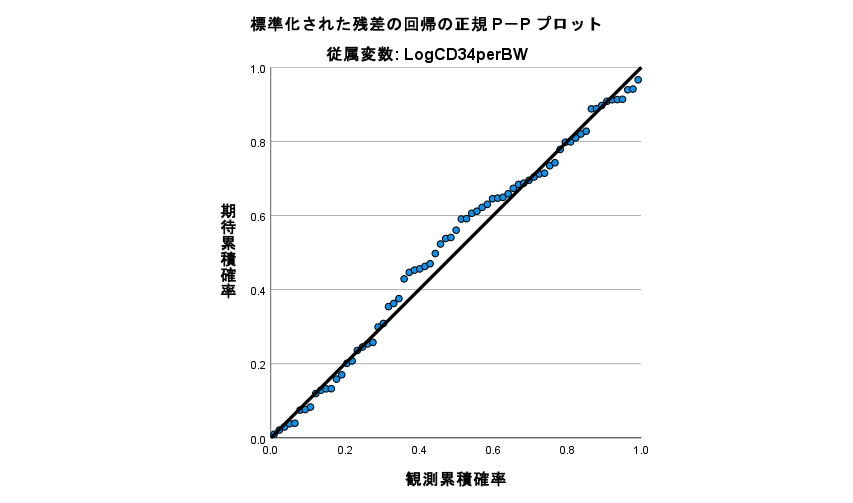
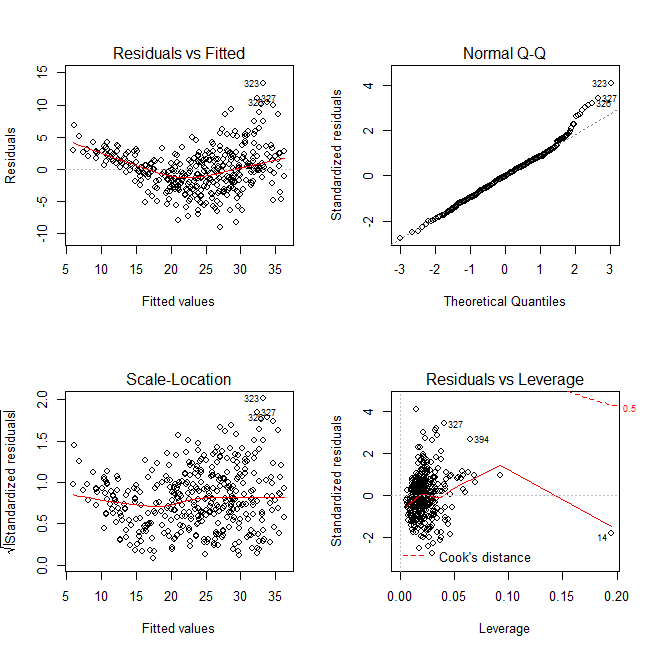
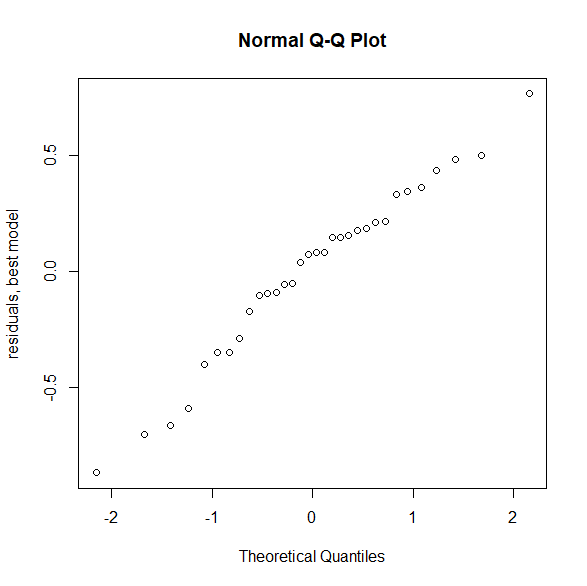
R と SPSS で重回帰分析の残差が正規分布であるのを確認する方法
回帰分析をする際に、説明変数や目的変数が正規分布をしていないことで悩んでいる人は多い。 悩むところはそこじゃない。 重回帰分析では、残差が正規分布している必要がある。 重回帰分析の前提は何か? 重回帰分析の前提は4つある。 独立性(データそれ... -

t 検定と分散分析と回帰分析は同じことをしている
分散分析と回帰分析とt検定は同じものである。 これがわかれば、重回帰分析(共分散分析)が交絡因子調整した群間比較に使われる理由がわかるだろう。 t検定は回帰分析でもできるし、分散分析は二群でもできる ここで、t検定は、いわゆる t 検定のこと... -

R で行列計算を使って重回帰分析を行う方法
重回帰分析は行列計算をしているわけだが、実際どのような計算をしているのか、R を使って計算してみる。 サンプルデータの準備 使用するデータは ISLR パッケージの Carseats データ。 これはチャイルドシートの売り上げデータ。 パッケージのインストー... -

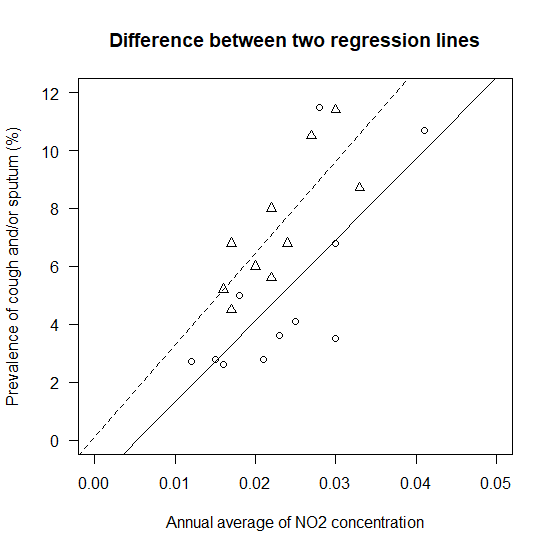
R で回帰直線の差の検定を行う方法
二つのデータセットがあって、二つの回帰直線が描けたとき、そのあとどうすればいいか? そのあとは、傾きが同じと言えるか?さらには切片が同じと言えるか?と進んでいく。 二つの回帰直線の差を検定してみる。 回帰直線の差の検定のためのサンプルデータ... -

R で重回帰分析を行う具体例 ― ISLR パッケージ Auto データセットを使った重回帰分析
R の ISLR パッケージの Auto データセットを使った分析例。 データの準備 最初の一回だけ、ISLRパッケージをインストール。 install.packages("ISLR") ISLRパッケージを呼び出して、解析開始。 library(ISLR) ISLRパッケージのAutoデータセットを用いて解... -

相関と回帰の違いは何か?
相関と回帰はどう違うか? 両方とも2つのデータの関係性を見ているわけで、とても似ている。相関と回帰の違いについて、まとめてみる。 相関と回帰の根本的な違いは? 相関は、相関係数が中心で、 データXとデータYの お互いの関係性を見る。 相関分析には... -

R で重回帰分析の変数選択に参考となる計算上ベストな変数セットを提案してくれる方法
R で重回帰分析を行った際の変数選択の方法の解説。 bestglmの準備とサンプルデータ R の bestglm() 関数は、AIC, BIC(デフォルト), BICqなどの Information Criterion 情報規準を使って ベストの変数の組み合わせを見つけてくれる。 bestglmパッケージのz...
1