Cox 回帰で必要な、比例ハザード性を確認する方法の解説
比例ハザード性を二重対数プロットで確認する方法
EZRで比例ハザード性を確認する方法の一つ目として、グラフで確認する方法がある。
二重対数プロット( Complementary log-log plot )というものを描く。
通常のカプランマイヤー曲線のRスクリプトを応用して簡単に描ける。
まず解析データを用意したら、「統計解析」→「生存期間の解析」→「Logrank検定」を選択する。
観察期間変数、イベント変数、群別変数を選択しOKをクリックすると、カプランマイヤー曲線が描かれる。
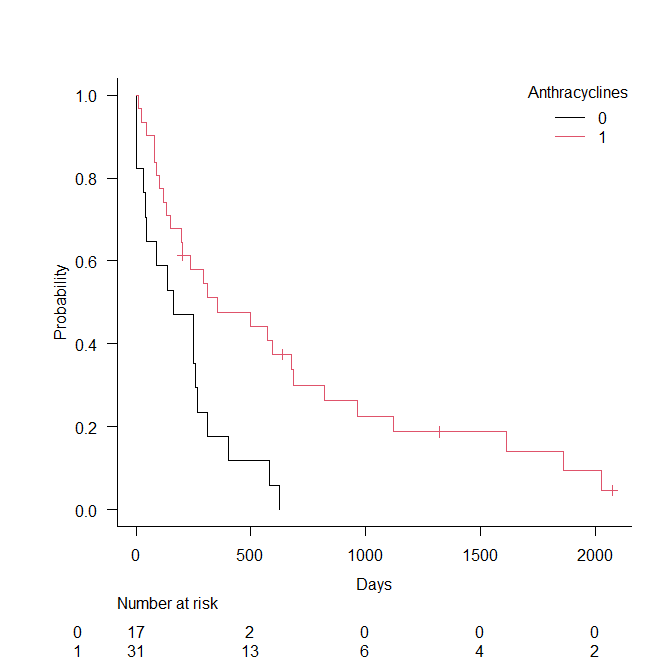
カプランマイヤー曲線の例
このときRスクリプトの枠には以下のようなスクリプトが出力されている。
plot(km, bty="l", col=1:32, lty=1, lwd=1, conf.int=FALSE, mark.time=TRUE,
xlab="Days", ylab="Probability")
xticks <- axTicks(1)
n.atrisk <- nrisk(km, xticks)
for (i in 1:length(km$strata)){axis(1, at = xticks, labels = n.atrisk[i,],
line=3+i, tick = FALSE)}
for (i in 1:length(km$strata)){mtext(legend[i], at=-(xticks[2]-xticks[1])/2,
side=1, line=4+i, cex=1)}
title(xlab = "Number at risk", line = 3.5, adj = 0)
legend ("topright", legend, col=1:32, lty=1, lwd=1, box.lty=0,
title="Anthracyclines")
ここで最初の2行のplot()の最後に、fun="cloglog"を加筆して、全体を選択して実行をクリックする。
加えて、下から2行目のlegend()内のtoprightをbottomrightに変更して、legend (凡例) がグラフと被らないようにするとよい。
plot(km, bty="l", col=1:32, lty=1, lwd=1, conf.int=FALSE, mark.time=TRUE,
xlab="Days", ylab="Probability", fun="cloglog")
xticks <- axTicks(1)
n.atrisk <- nrisk(km, xticks)
for (i in 1:length(km$strata)){axis(1, at = xticks, labels = n.atrisk[i,],
line=3+i, tick = FALSE)}
for (i in 1:length(km$strata)){mtext(legend[i], at=-(xticks[2]-xticks[1])/2,
side=1, line=4+i, cex=1)}
title(xlab = "Number at risk", line = 3.5, adj = 0)
legend ("bottomright", legend, col=1:32, lty=1, lwd=1, box.lty=0,
title="Anthracyclines")
そうすると以下のようなグラフが描かれる。
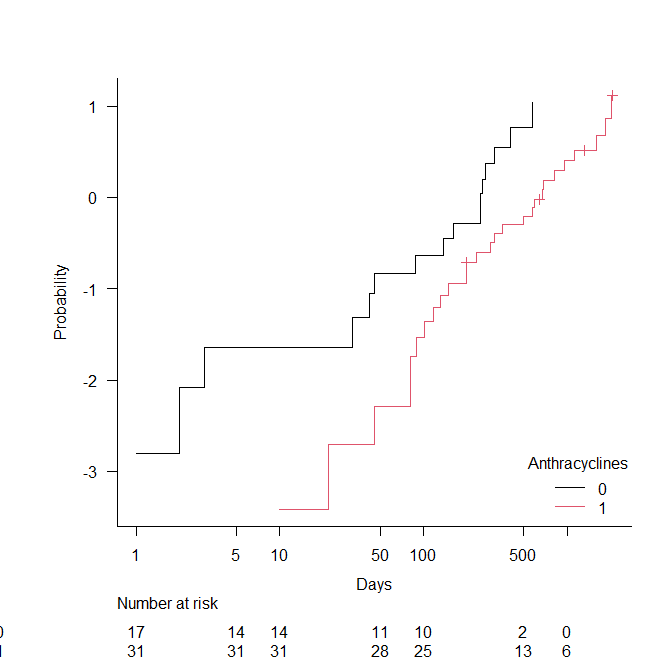
Complementary log-log plotの例
2本の階段状のグラフが、おおよそ平行になっていれば、比例ハザード性が満たされていると言える。
この例は、比例ハザード性が満たされていると言えるレベルと思う。
このようにして、グラフによって視覚的に確認する方法が一つ目の方法だ。
二重対数の意味
Complementary log log の意味は、0 から 1 の確率を無限小から無限大に変換するということである
グラフを描いてみるとわかる
X 軸に確率(0 から 1)、Y 軸に complementary log log を施した 確率(-∞ から ∞)を取ってプロットすると以下のようになる
prob <- 1:999/1000
cloglog <- log(-log(prob))
plot(cloglog ~ prob, xlab="Probability", ylab="log(-log(Probability))")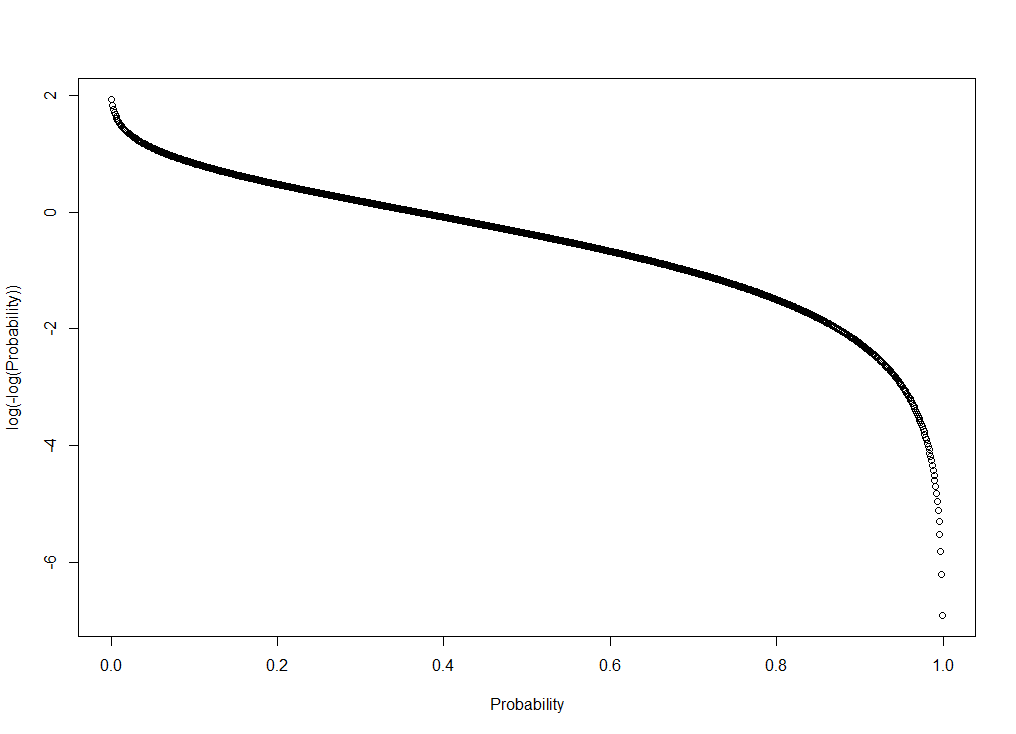
比例ハザード性を検定で確認する方法
EZRで比例ハザード性を確認する方法の二つ目は、検定を用いる方法だ。
「統計解析」→「生存期間の解析」→「Cox回帰」を選択する。
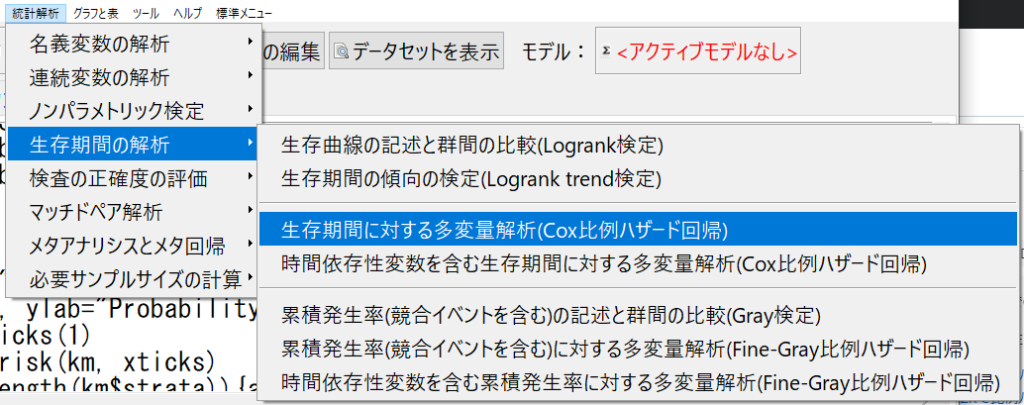
「統計解析」→「生存期間解析」→「Cox回帰」を選択
時間変数、イベント変数、説明変数を選択投入する。
カプランマイヤー曲線を描いた時に用いた、観察期間変数、イベント変数、群別変数と同じ変数を選択する。
比例ハザード性の分析を行うにチェックを入れて、OKをクリックする。

比例ハザード性の分析を行うにチェック
cox.zph() という関数で、検定される。
帰無仮説は、比例ハザード性が満たされている、というもの。
統計学的有意でなければ、比例ハザード性が満たされていないとは言えない、つまり消極的に比例ハザード性が満たされていると言ってもいいということになる。
結果は以下のように表示される。
> print(cox.zph(CoxModel.1))
chisq df p
Anthracyclines 0.609 1 0.44
GLOBAL 0.609 1 0.44
検定の本来の目的は、帰無仮説が棄却されることなのに、帰無仮説が棄却されないことが目的である検定シリーズ(正規性の検定、等分散性の検定、球面性の検定等)の一つで、おすすめの方法ではない
まとめ
EZRで生存時間解析を実施する際に検討したい比例ハザード性の確認方法を2つ紹介した。
個人的には complementary log-log plot で視覚的に確認すれば十分と思っている。
検定は、サンプルサイズが大きい場合、ほんの少しのずれでも検出してしまい、適切ではないからだ。
正規性の確認と同様に、どんなときもまずはグラフで視覚的に確認することが最優先という一例である。
何らか参考になれば。
おすすめ書籍








コメント