重回帰モデルの評価指標の決定係数とモデルの有意性の分散分析の検定はどのように使い分ければよいのか?
決定係数とは?
決定係数とは、推定された重回帰モデルが実際のデータにどの程度当てはまっているかを表す指標である。
0から1の範囲の数値をとり、1が完全に当てはまっていると解釈する。
計算式は以下のとおりである。
$$ R^2 = \frac{\sum (\hat{y} – \bar{y})^2}{\sum (y – \bar{y})^2} $$
$ R^2 $ は決定係数を表すときに用いられる一般的な表記である。
y が、従属変数の実測値、$ \bar{y} $ が、従属変数の実測値の平均値、$ \hat{y} $ が、従属変数の予測値である。
従属変数の予測値は、重回帰モデルで予測した値である。
ちなみに、イメージをつかみやすいように式をシンプルにする目的で、添え字は省略してある。
この式がどこから来たのかと言うと、以下の式から来ている。
$$ \sum (y – \bar{y})^2 = \sum (\hat{y} – \bar{y})^2 + \sum (y – \hat{y})^2 $$
これは従属変数の全変動を、回帰で説明できる変動と残差の変動に分けることができるという式である。
左辺が従属変数の全変動、右辺の第1項が回帰による変動、第2項が残差による変動である。
両辺を、左辺の従属変数の全変動で割ると、右辺の第1項が決定係数になる。
$$ \frac{\sum (y – \bar{y})^2}{\sum (y – \bar{y})^2} = \frac{\sum (\hat{y} – \bar{y})^2}{\sum (y – \bar{y})^2} + \frac{\sum (y – \hat{y})^2}{\sum (y – \bar{y})^2} $$
決定係数は、回帰変動が全変動に対してどれだけの割合を占めるか(それゆえ、寄与率とも言われる)、ということを意味している。
右辺第 1 項と左辺を入れ替えて符号も入れ替えると、以下のようにもなる
$$ \frac{\sum (\hat{y} – \bar{y})^2}{\sum (y – \bar{y})^2} = 1 – \frac{\sum (y – \hat{y})^2}{\sum (y – \bar{y})^2} $$
つまり、残差変動が小さい(予測値が実測値に近い)と、右辺第 2 項が小さくなり、決定係数は 1 に近づく
決定係数が 1 に近づくと、回帰変動が全変動に近い、つまり、重回帰モデルで、全変動の多くの部分を説明できる、すなわち、重回帰モデルがデータに当てはまっている、というふうに解釈するわけである。
決定係数は、1 に近いとより当てはまっているという評価が可能である点で、指標としてわかりやすい。
ちなみに、決定係数がどのくらいであればよいかは、過去記事参照。

モデルの有意性の分散分析
では、重回帰モデルの有意性の分散分析はどのようになっているか。
重回帰モデルの有意性の分散分析というのは、重回帰モデルの統計学的有意性の検定である。
帰無仮説は、「重回帰モデルは統計学的に意味がない」。
有意水準5%で棄却されれば、重回帰モデルが統計学的に意味がある、と言える。
重回帰モデルの有意性の分散分析は以下のように計算される。
| 変動の種類 | 平方和 | 自由度 | 平均平方 | F | 有意確率 |
|---|---|---|---|---|---|
| 回帰 | $ \sum (\hat{y} – \bar{y})^2 $ | m | \begin{align} \frac{\sum (\hat{y} – \bar{y})^2}{m} \\ = MS_{REG} \end{align} | $$ \frac{MS_{REG}}{MS_{ERR}} $$ | p |
| 残差 | $ \sum (y – \hat{y})^2 $ | n – m – 1 | \begin{align} \frac{\sum (y – \hat{y})^2}{n – m – 1} \\ = MS_{ERR} \end{align} | ||
| 全体 | $ \sum (y – \bar{y})^2 $ | n – 1 |
ここでも変動が登場する。
回帰の変動と全体の変動の比が、決定係数であることは上記で述べたが、決定係数に登場する変動がこちらにも登場しているわけである。
ここで、回帰変動の自由度 m は、独立変数の数である。
n はサンプルサイズである。
変動は平方和とも呼ばれる。
何かの差の2乗(平方)の合計(和)になっているからである。
自由度で割ると平均平方と呼ばれる。
回帰の平均平方( $ MS_{REG} $)と残差の平均平方($ MS_{ERR} $)の比が、F分布に従うF値であり、その検定結果が有意確率pとなる。
なので、回帰と残差の比ではあるものの、決定係数とよく似た計算をしているのがわかる。
決定係数とモデル有意性の分散分析の違いは何か?
決定係数は全体の変動のうち、回帰の変動がどのくらいを占めているかというものだったのに対し、モデルの有意性の分散分析は、回帰の変動が残差の変動(全体の変動からの差分)よりどのくらい大きいかで、回帰モデルの有意性を検討する形になっている。
つまり、決定係数もモデルの分散分析も、同じような計算値を用いて、同じようなことを示していると言える。
ただ、決定係数は大小が検討できる数値であるのに対し、モデルの有意性の分散分析は有意水準以下かどうかで統計学的有意かどうかしかわからないという点が大きな違いである。
しかしながら、どちらか一つあれば決定的ということはないため、どちらの指標も重要な指標である。
ゆえに、使い分けるわけではなく、常に同時に計算して提示するのが良い。
事実、EZRでは、同時に出力される。
報告する際にもどちらも提示するとよいだろう。
EZRの出力結果で確認してみる
以下は、EZRでの出力例である。
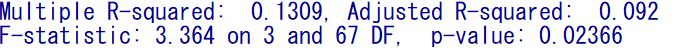
このように決定係数0.1309、とモデルの有意性の分散分析の結果としてF値とp値が同時に出力される。
この重回帰モデルの分散分析表を表示してみると以下のようになる。
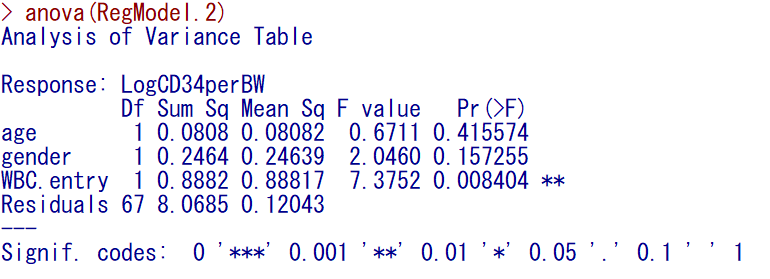
この値を使って回帰の変動を計算すると1.2154(= 0.0808 + 0.2464 + 0.8882)と計算される。
また、全体の変動は、9.2839(= 1.2154 + 8.0685)と計算される。
回帰の変動と全体の変動の比を取ると0.1309148(= 1.2154 / 9.2839)となり、決定係数0.1309と一致する。
以下は、Rのコンソールで計算した結果である。
> 0.0808+0.2464+0.8882
[1] 1.2154
> 0.0808+0.2464+0.8882+8.0685
[1] 9.2839
> 1.2154/9.2839
[1] 0.1309148
このように決定係数とモデルの有意性の分散分析はつながっている。
まとめ
重回帰モデルの評価としての決定係数とモデルの有意性の分散分析について、詳しく見てきた。
どちらも回帰モデルの当てはまり(回帰変動)をもとに、指標化した数値で表すか、検定で統計学的有意性を検討しているかの違いと言える。
どちらか一方で必要十分ということでもないため、使い分けるということでもなく、重回帰モデルの評価指標として、どちらも提示するのがよい。
参考になれば。
参考サイト
27-5. 決定係数と重相関係数 | 統計学の時間 | 統計WEB
27-6. 回帰の有意性の検定 | 統計学の時間 | 統計WEB
参考書籍
SPSSによる応用多変量解析
EZR公式マニュアル







コメント