ロジスティック回帰の回帰診断の一つにROC曲線を活用する方法がある。
ロジスティック回帰モデルを多変量で行えば多変量ROC曲線となる。
モデルごとに算出されるROC曲線を比較するにはどのようにすればよいか？
ROC曲線とは？
まずROC曲線とは何か？
ROC曲線とは、あり・なし、高い・低い、正解・間違いなど２値を判別するための連続量の切れ目（閾値[しきいち]、カットオフポイント）を検討する方法だ。
ROCとはReceiver Operating Characteristicsという言葉の頭文字だが、もともとのレーダー技術からの派生で、主に臨床検査の感度・特異度に使われている。
ある数値以上を、病気ありと定義すると、感度・特異度がどのくらいになるか？
どの数値がもっとも感度・特異度のバランスがいいか？
などの分析を行うものだ。
ロジスティック回帰の多変量 ROC 曲線とは？
ROC曲線は、一つの連続量で、あり・なしを予測する性能の検討なのだが、一つの連続量を多変量から予測した確率という数値にして、２値の目的変数（例えば病気あり・なし）を予測する性能というふうに考えたのが、多変量ROC曲線になる。
ある病気の有り無しを、ある一つの検査値と、それを補助する検査値、性別、年齢、BMIなどの変数で総合的に計算される確率で予測するというような形になる。
総合的に確率を計算するときの変数を、増やしたり、減らしたりすると、いくつか確率が求まる。
どの組み合わせの時にもっとも予測性能が良いかという比較をすることができるというわけである。
EZRで多変量ROC曲線を描くには？
多変量ROC曲線を描くには、ロジスティック回帰分析のプログラムで、傾向スコア算出の機能を借りる。
まず、「統計解析」→「名義変数の解析」→「ロジスティック回帰」でプログラムを選ぶ。
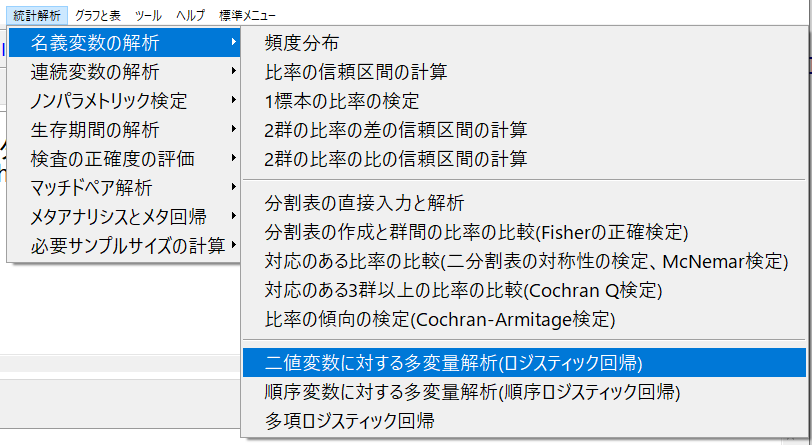
ロジスティック回帰モデルに投入する変数を選んで、傾向スコア変数を作成するチェックボックスにチェックを入れる。
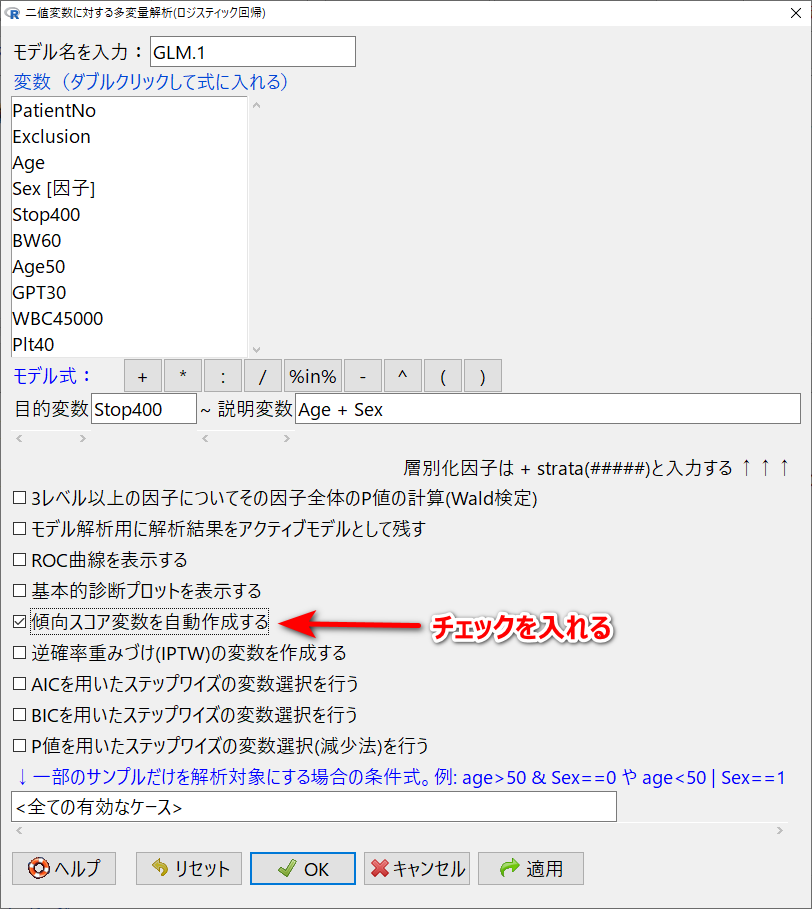
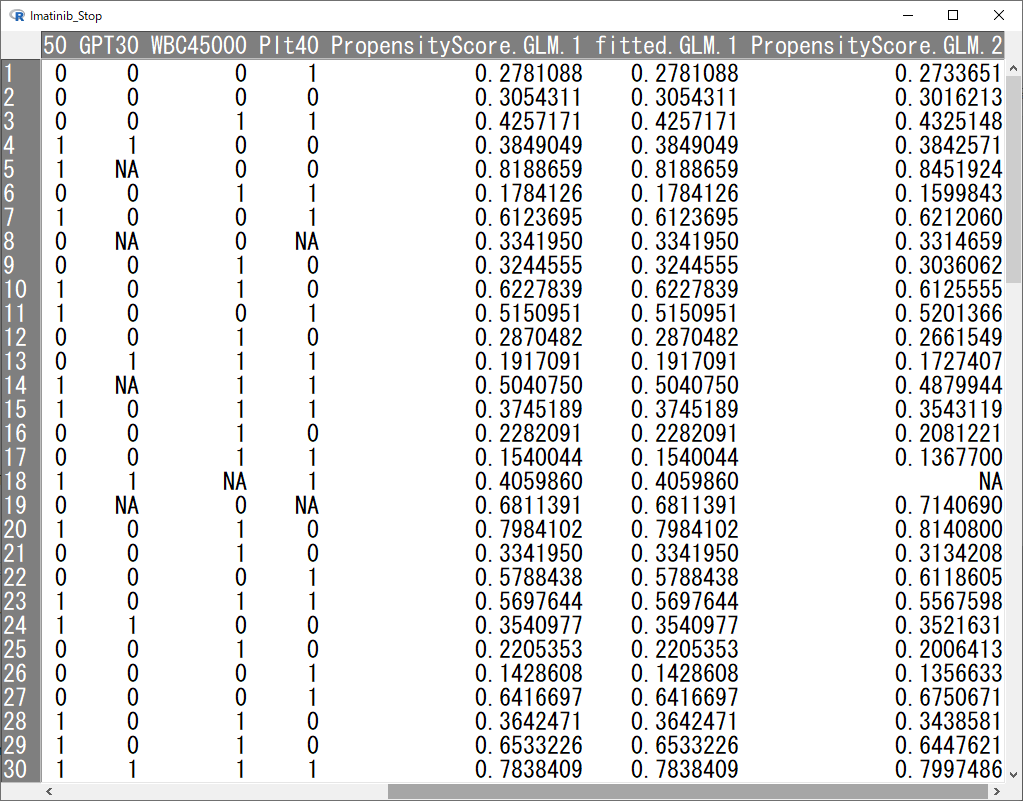
OKをクリックすると、傾向スコア（PropensityScore.GLM.1）という名前の変数が作られる（最後の数字は何度も作成していると変わる）。
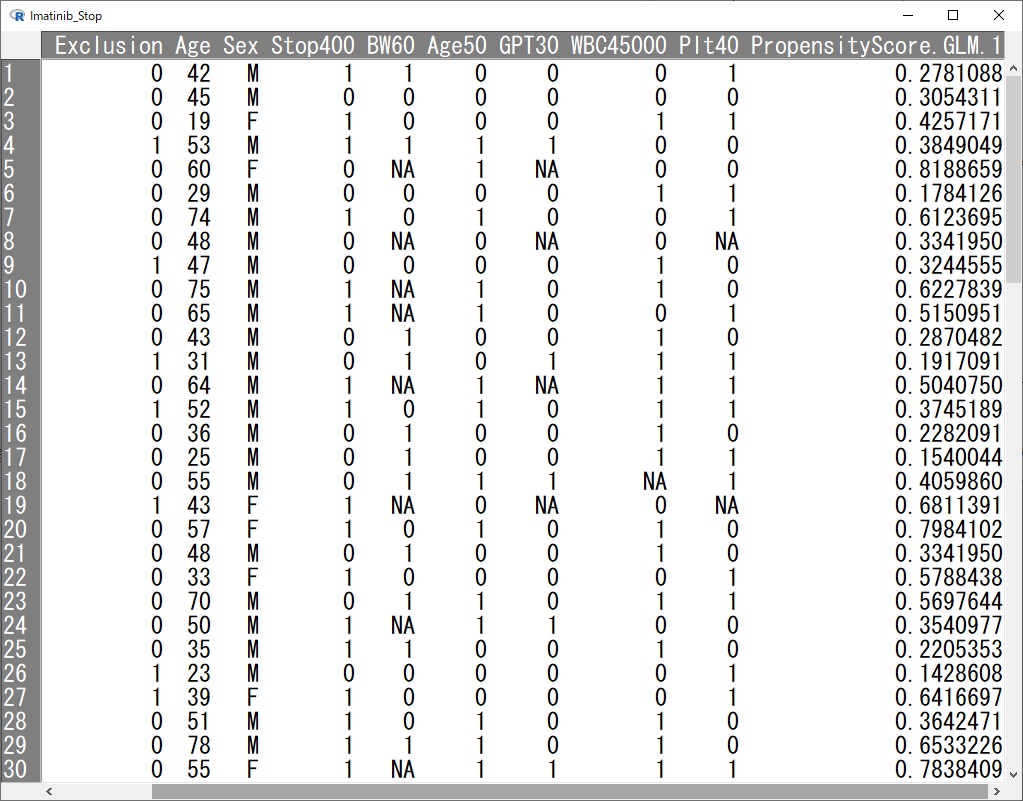
2つの多変量ROC曲線を比較するには？
もう一つ多変量ROC曲線のための確率を計算する。
先ほどよりも一つ変数を増やして、再度傾向スコアを作成する。
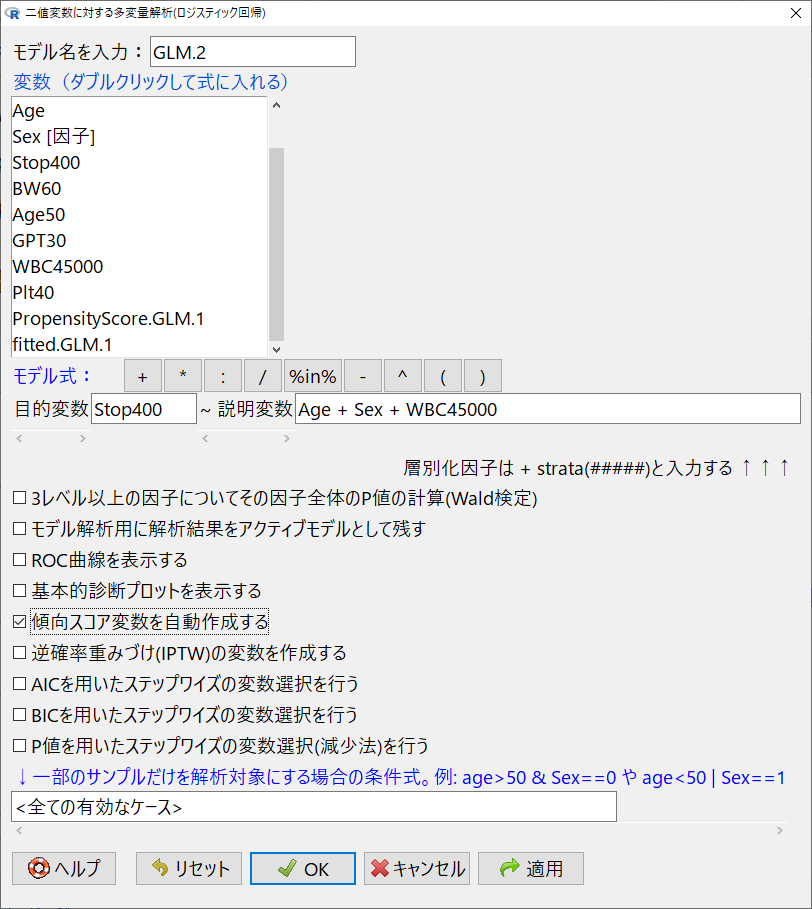
PropensityScore.GLM.2がGLM1とは少しだけ違うのがわかる。
このあとは、２つのROC曲線を比較メニューを使用して、比較する。
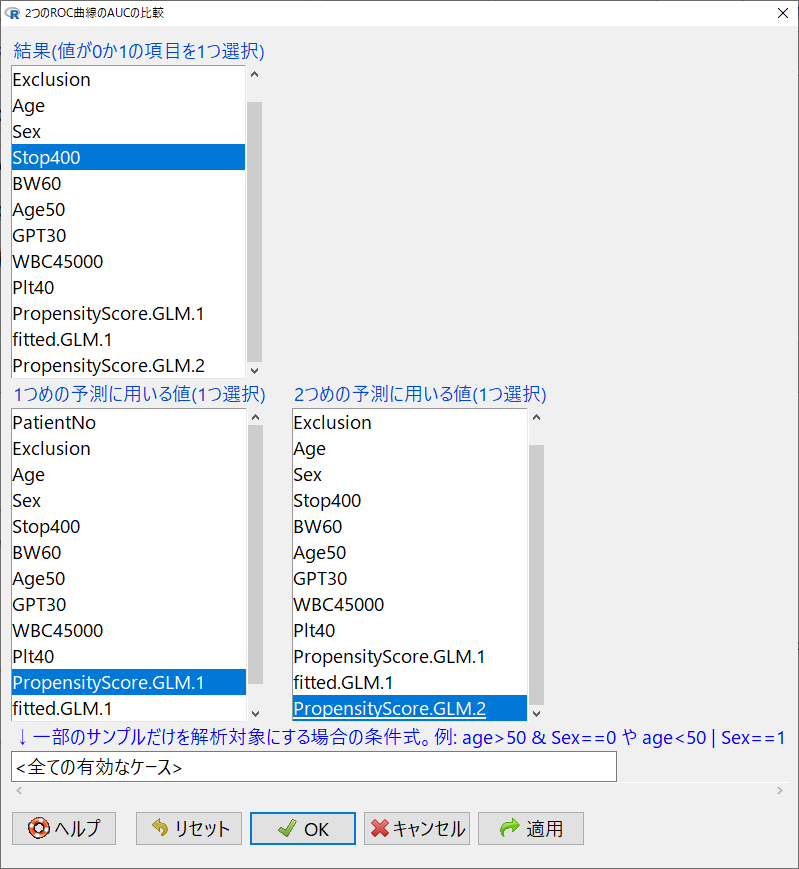
結果の枠は、目的変数を選択、１つ目の予測と２つ目の予測で、それぞれ、PropensityScore.GLM.1とPropensityScore.GLM.2を選択する。
OKをクリックすると、解析結果とグラフが表示される。
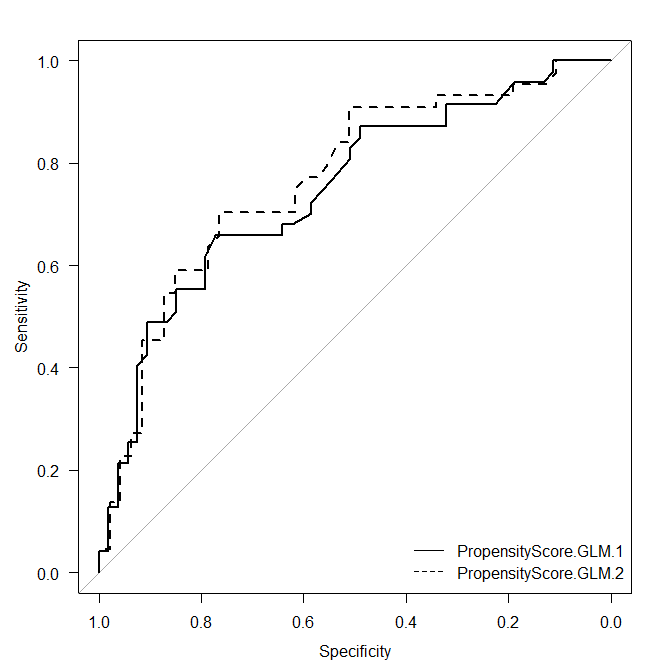
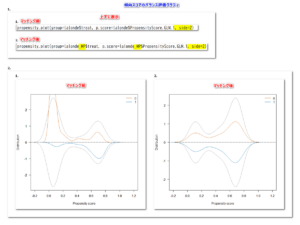
X 軸を、通常の 1 – Specificity にしたい場合、R のスクリプトの下記黄色ハイライト部分に legacy.axes=TRUE と加筆して、切り抜いている部分を再度実行すると、通常の X 軸になる。
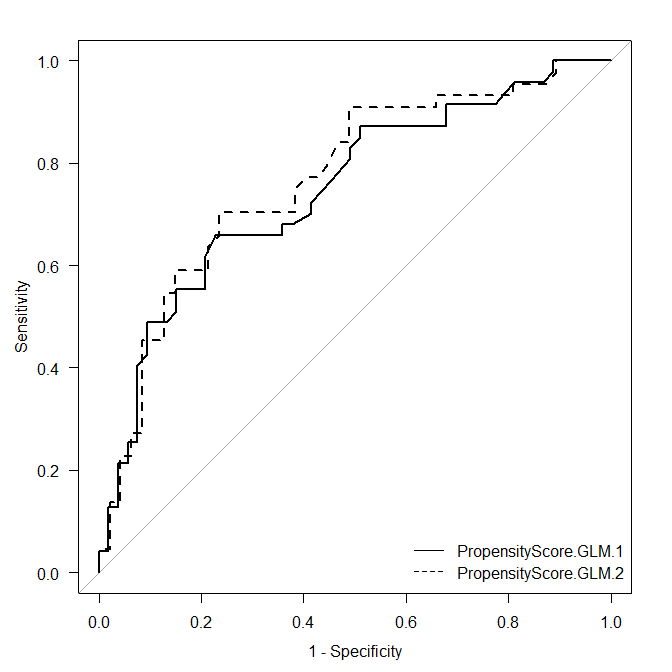
グラフを見ると、ほぼ同様で、解析結果を見ると統計学的に異なっているとは言えないことがわかる。
このように2つの多変量ROC曲線を比較することができる。
もし、統計学的に異なるようであれば、追加した変数はモデルの予測性能を向上したと言えるかもしれない。
いろいろと試してみて、性能の良いモデルを探るという試行錯誤を行う。
まとめ
多変量ROC曲線とは、ロジスティック回帰分析の目的変数の予測値としての確率を使って、目的変数をどの程度感度・特異度よく推測できるかという、ロジスティック回帰モデルの予測能の診断に使える。
どちらがよりよく予測できるかの比較は、EZRを使って、各モデルの傾向スコア（Propensity Score）を計算するプログラムを活用し、その後2つのROC曲線を比較するメニューを使うことで簡単に実行できる。
参考書籍
見やすい図解と楽しいイラストで、EZRによる医療統計を短期間で学べる本
EZRをしっかり使いこなしたい本格派向けEZR公式マニュアル
コメント