EZR で共分散分析を行い回帰直線を比較する方法

共分散分析を使えば、2つの回帰直線の傾きや切片が異なるかどうか検討できる。

直接的な傾きの差の検定や切片の差の検定ではないが、同様な結果が簡単に得られるので、共分散分析でよいと思っている。

データの準備

こちらを題材として、EZRで再解析してみる。

データはこのように準備する。

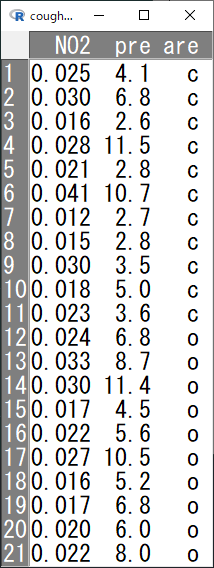
Rスクリプトはこちら。

NO2.c <- c(0.025,0.030,0.016,0.028,0.021,0.041,0.012,0.015,0.030,0.018,0.023)
pre.c <- c(4.1,6.8,2.6,11.5,2.8,10.7,2.7,2.8,3.5,5.0,3.6)
are.c <- rep("c",length(NO2.c))
NO2.o <- c(0.024,0.033,0.030,0.017,0.022,0.027,0.016,0.017,0.020,0.022)
pre.o <- c(6.8,8.7,11.4,4.5,5.6,10.5,5.2,6.8,6.0,8.0)
are.o <- rep("o",length(NO2.o))
cough.prev.c <- data.frame(NO2=NO2.c,pre=pre.c,are=are.c)
cough.prev.o <- data.frame(NO2=NO2.o,pre=pre.o,are=are.o)
cough.prev <- rbind(cough.prev.c,cough.prev.o)

散布図と回帰直線を描く

層別の散布図を描かせてみる。

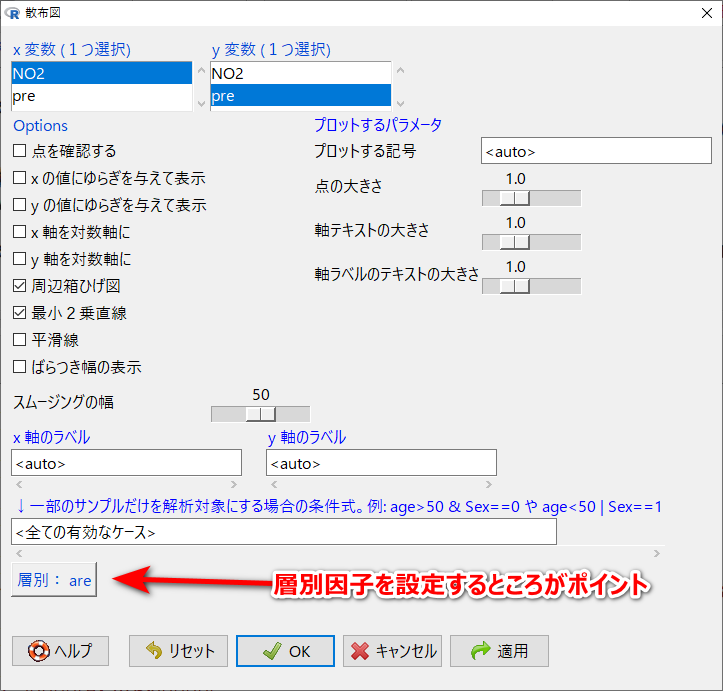
「グラフと表」から「散布図」を選択。

XにNO2、Yにせき・たんの有症割合 pre (prevalence) を選択する。

設定のポイントは、層別因子の設定。

層別因子は、are (area)である。

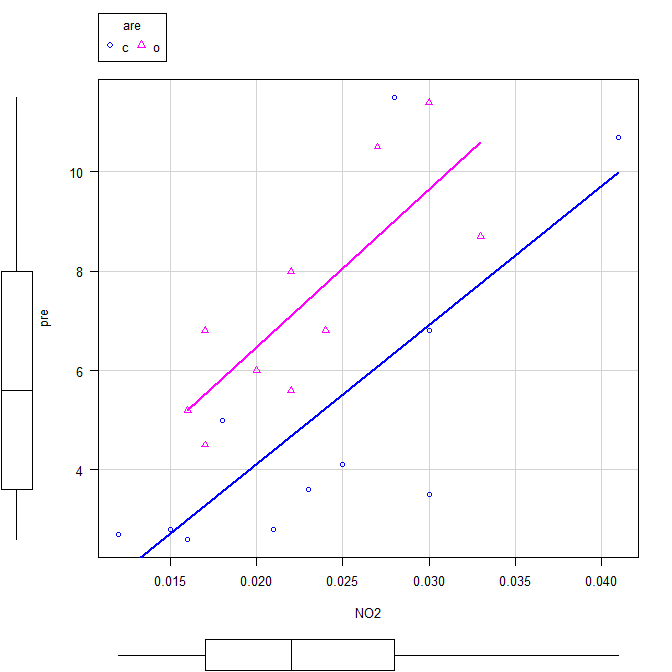
これなら傾きは異ならなそうであることが想像される。

共分散分析を実施する

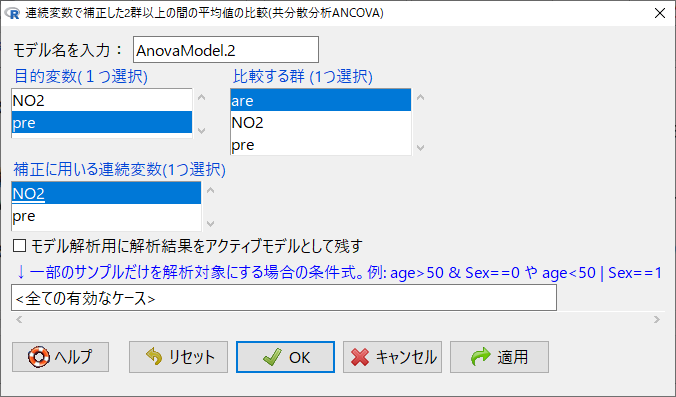
「統計解析」→「連続変数の解析」→「共分散分析ANCOVA」を選択して、共分散分析を実施する。

目的変数がpre、比較する群はare、補正に用いる変数がNO2とする。

交互作用はp=0.783で統計学的有意ではなく、are別には傾きが違わないことが分かった。

areの効果は統計学的有意なので、2群で切片は異なることがわかった。

グラフを見れば一目瞭然ではある。

NO2も有意なので、傾きも意味がある。

つまりは、NO2が高くなるにつれて、せき・たんの有症割合も高くなると言える。

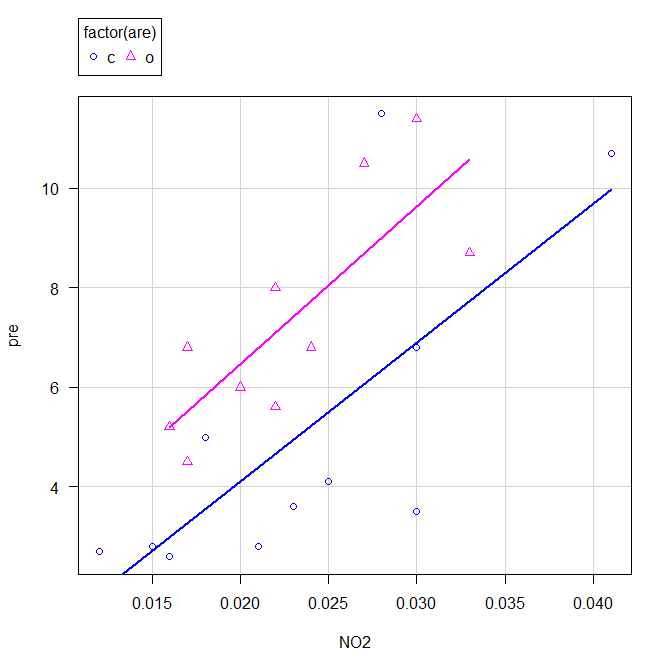
それを表しているのが先ほどの2本の回帰直線がひかれた散布図である。

共分散分析を実施すると自動で描かれた。

まとめ

２つの回帰直線の比較は、共分散分析を使うと簡単に実施できる。

EZRで共分散分析を実施し、グラフを描かせるのはとても簡単だ。

参考になれば。

おすすめ書籍

EZR公式マニュアル