R で競合リスク分析 Gray 検定を行う方法

競合リスクとは何か？

Gray 検定の実行方法

競合リスクとは？

再発がエンドポイントであったが、再発する前に死亡してしまったので、観察できなかった。

脳梗塞の発現がエンドポイントだったが、先に肺炎でお亡くなりになり、観察できなかった。

このように、再発をエンドポイントにした場合の再発前の死亡、あるいは、脳梗塞の発生をエンドポイントにした場合のその他の原因による死亡、こんなふうなイベントが発生するリスクを競合リスクと呼ぶ。

生存時間解析において、競合リスクがある場合、どのように解析すればよいか？

競合リスク分析のサンプルデータの準備

競合リスクがある場合、生存確率が下がっていくカプランマイヤー曲線の代わりに、累積的にイベントが発現していく様を累積発現グラフに描く。

統計ソフトRの riskRegression パッケージの Melanoma データを用いる。

パッケージはcmprsk と riskRegression を事前にインストールしておく。

library(cmprsk)
library(riskRegression)
library(survival)
head(Melanoma)

Melanoma データのうち、以下の 3 つの変数を主に使う。

1. イベントまでの時間変数 time
2. 状態の変数 status (0が単なる研究終了の打ち切り、1がメラノーマによる死亡（研究したいエンドポイント）、2がメラノーマ以外による死亡（競合リスク）)
3. 浸潤 invasion （レベル０，１，２で、2が重症）

> head(Melanoma)
time status                    event invasion ici      epicel       ulcer thick
1   10      2       death.other.causes  level.1   2     present     present  6.76
2   30      2       death.other.causes  level.0   0 not present not present  0.65
3   35      0                 censored  level.1   2 not present not present  1.34
4   99      2       death.other.causes  level.0   2 not present not present  2.90
5  185      1 death.malignant.melanoma  level.2   2     present     present 12.08
6  204      1 death.malignant.melanoma  level.2   2 not present     present  4.84
sex age   logthick
1   Male  76  1.9110229
2   Male  56 -0.4307829
3   Male  41  0.2926696
4 Female  71  1.0647107
5   Male  52  2.4915512
6   Male  28  1.5769147

競合リスクの累積発現曲線を描いてみる

エンドポイント（status==1）と競合リスク（status==2）の累積発現曲線（Cumulative Incidence Curve）を描いてみる。

Surv()とsurvfit()の組み合わせでfun=”event”を使って簡易的に描くことはできるが、cmprsk パッケージのcuminc()を使うほうが適切。

cuminc()をより使いやすくしたCumIncidence()もある。

survfit0.1 <- survfit(Surv(time,status==1)~1,
data=Melanoma)
survfit0.2 <- survfit(Surv(time,status==2)~1,
data=Melanoma)
layout(matrix(1:4,nr=2))
plot(survfit0.1, fun="event", conf.int=FALSE)
plot(survfit0.2, fun="event", conf.int=FALSE, col=2)
cuminc0 <- cuminc(ftime=Melanoma$time,
fstatus=Melanoma$status)
plot(cuminc0)
source("http://www.stat.unipg.it/luca/misc/CumIncidence.R")
CumIncidence(ftime=Melanoma$time, fstatus=Melanoma$status)

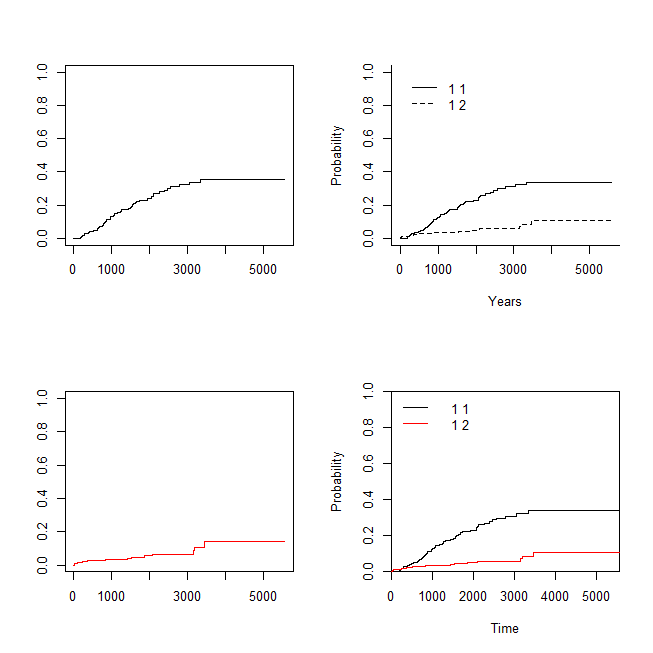
左側の上下2つがSurv()とsurvfit()を使ったグラフ。

右上がcuminc()のデフォルトグラフ。右下がCumIncidence()のグラフ。

cuminc()は、statusの2つがline types (lty)で描き分けられている。

一方でCumIncidence()のグラフは、statusが黒と赤で塗り分けられている。

競合リスクの要因別累積発現

次に、invasionの3レベル別の累積発現と検定の結果。

累積発現グラフは、以下のスクリプトで書ける。

survfit1.1 <- survfit(Surv(time,status==1)~invasion,
data=Melanoma)
survfit1.2 <- survfit(Surv(time,status==2)~invasion,
data=Melanoma)
layout(matrix(1:4,nr=2))
plot(survfit1.1, fun="event", conf.int=FALSE, lty=1:3)
plot(survfit1.2, fun="event", conf.int=FALSE, lty=1:3,col=2)
cuminc1 <- cuminc(ftime=Melanoma$time,
fstatus=Melanoma$status, group=Melanoma$invasion)
plot(cuminc1)
(CumInc1 <- CumIncidence(ftime=Melanoma$time,
fstatus=Melanoma$status, group=Melanoma$invasion))

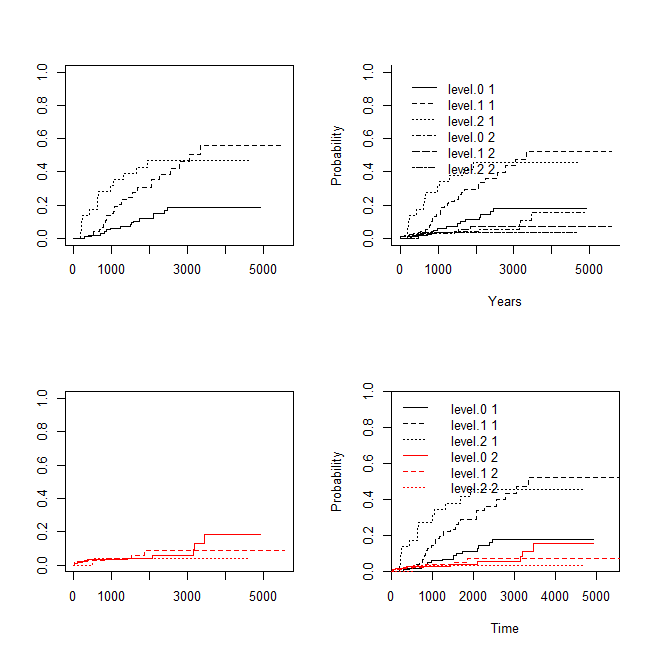
左の上下二つはSurv()とsurvfit()で描いたグラフ。

invasionの3レベルltyで描き分けている。

右上はcuminc()で描いたCumulative Incidenceのグラフ。

statusが2つとinvasionが3レベルの合計6本がltyで描き分けられている。

右下はCumIncidence()で描かれたもの。statusが黒と赤で分けられていて、それぞれltyでinvasionのレベルがわかるようになっている。

CumIncidence()が一番見やすい。

競合リスクの Gray 検定（ログランク検定との比較）

survdiff()の結果とcuminc()の結果を比べてみる。

survdiff1.1 <- survdiff(Surv(time,status==1)~invasion,
data=Melanoma)
survdiff1.2 <- survdiff(Surv(time,status==2)~invasion,
data=Melanoma)
survdiff1.1
survdiff1.2
cuminc1
CumInc1

以下の 4 つの出力の塊のうち、上二つがsurvdiff()の結果、つまりログランク検定の結果である。

エンドポイント(status==1)と競合リスク(status==2)を別々に解析している。

下の二つ cuminc1 及び CumInc1はともに同じ結果でこちらは Gray 検定の結果。

> survdiff1.1
Call:
survdiff(formula = Surv(time, status == 1) ~ invasion, data = Melanoma)
Chisq= 18.8  on 2 degrees of freedom, p= 8e-05
> survdiff1.2
Call:
survdiff(formula = Surv(time, status == 2) ~ invasion, data = Melanoma)
Chisq= 0.5  on 2 degrees of freedom, p= 0.8
> cuminc1
Tests:
stat           pv df
1 17.9441643 0.0001269037  2
2  0.8846449 0.6425424207  2
> CumInc1
$test
Statistic df   p-value
1 17.9441643  2 0.0001269
2  0.8846449  2 0.6425424

Gray 検定のほうが、エンドポイントの有意確率が若干高い程度でほとんど同じであったが、理屈の上では、Gray 検定を行うのが望ましい。

まとめ

エンドポイントを観察したくても、その前に観察できなくなる事象が起きることがあり、そういう事象を競合リスクと呼ぶ。

競合リスクを加味した累積発現でグラフを描き、グループ間の差を見る場合は Gray 検定を行う。

統計ソフトRの場合、survival パッケージに加え、cmprsk パッケージのインストールが必要となる。

解説動画：EZR で Gray 検定を行う方法

EZR公式マニュアル