EZR で IPTW Fine-Gray 回帰を実施する方法

IPTW Fine-Gray 回帰を実施する方法

Fine-Gray 回帰とは？

Fine-Gray 回帰とは、競合リスクがある場合の多変量調整回帰モデルの一つ。

詳しくは以下をどうぞ。

IPTW とは？

IPTW とは、逆確率重みづけという意味である。

逆確率重み付けとは、逆確率という重みを付けて回帰分析を行うことを言っている。

重みを付けることで、1例の人数が、重みの分だけかさましされたことになる。

逆確率というのは、傾向スコアの逆数である。

こちらもどうぞ。

傾向スコアは、治療薬など、エンドポイントに影響を与える変数の発現確率を多変量で推定したもの。

IPTW は、傾向スコアを $ p $ として、ある治療薬で治療を受けた人は $ 1/p $ 、治療を受けなかった人は $ 1/(1-p) $ とする重みを付ける。

実際は治療を受けたのに、傾向スコア $ p $ は小さく、あたかも治療を受けなかった人のような傾向スコアを持っている人は、基本的には少ないため、その逆数、つまり大きい重みを与えて、人数を多くする。

逆に、治療を受けていないのに、傾向スコア $ p $ が大きく、あたかも治療を受けた人のような傾向傾向スコアを持っている人も少ないため、その場合は、傾向スコアを１から引いて、その逆数の重みを付けて、人数をかさましする。

EZRでは、さらに治療を受けた人、受けなかった人の割合をそれぞれにかけた、安定化を行った重みを計算してくれる。

IPTW Fine-Gray回帰 パッケージとデータの準備

EZRで、Rスクリプトを使って、逆確率重み付けを使ったFine-Gray回帰が実施可能である。

具体的には、timeregパッケージの comp.risk() 関数を使うと実行できる。

手順は以下の通り。

１．timeregパッケージをインストール

EZRのRスクリプト画面に install.packages(“timereg”) と入力し実行する。

出てきた窓内のJapanを選択しインストールする。

２．timeregパッケージの呼び出し

EZRのRスクリプト画面に library(timereg) と入力し、実行。

３．解析データを準備して、以下のような感じにRスクリプト窓に書いて実行

fg5 <- comp.risk(Event(DaysDFS, CompRisk)~const(Group1),
data=Data3, cause=1, weights=Data3$weight.ATE.GLM.4)
summary(fg5)

この例の場合は、観察時間変数がDaysDFS、競合イベント変数がCompRisk、比較したい群がGroup1、データセット名がData3、競合イベントのうち今計算したいイベントが１( cause=1)、重みがData3の中のweight.ATE.GLM.4という設定である。

調整したい変数が他にもある場合は +const() を増やしていく。

~const(Group1)+const(Covariate1)+const(Covariate2) などという具合である。

ちなみに、逆確率重み付けの重み weight.ATE.GLM.4（最後の番号は実行した状況で異なるので、あなたの実行環境では異なると思う） は、ロジスティック回帰を用いて事前に作成しておく。

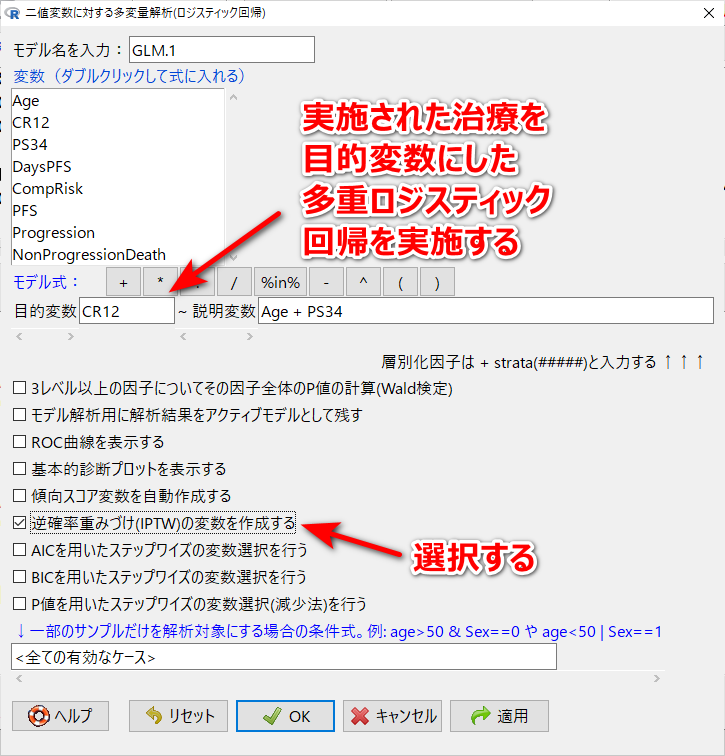
逆確率の重みを計算したあと、２つのステップが必要になった。

１つめは、一つでも欠損値があるケースを削除する必要があった。

２つめは、イベントまでの時間が０のケースを削除する必要があった。

以下がRスクリプトである。

#NAがある行を削除する
ALL_RIC <- na.omit(ALL_RIC)
#####指定した条件を満たす行だけを抽出したデータセットを作成する#####
ALL_RIC <- subset(ALL_RIC, subset=DaysPFS>0)

IPTW Fine-Gray 回帰の解析結果

あとは前述（及び下記再掲）のように R スクリプトに書いて実行する。

fg5 <- comp.risk(Event(DaysDFS, CompRisk)~const(Group1),
data=Data3, cause=1, weights=Data3$weight.ATE.GLM.4)
summary(fg5)

解析結果は以下の通り。

対数表示になっているので、真数表示にしたい場合は、以下のようにする。

まず、結果オブジェクト内のgammaが対数ハザード比（係数）である。

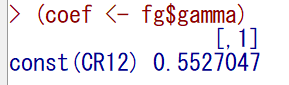
同様にvar.gammaが係数の分散である。

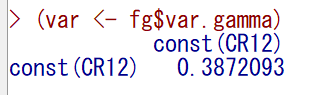
ちなみに、説明変数が複数ある場合は、分散共分散行列が表示される。

独立変数一つ一つの分散は、diag()で取り出す必要がある。

全然違う例だが、例えば以下のようにして分散を取り出す。

話を戻して、分散の平方根が標準誤差である。

標準誤差に1.96（標準正規分布の上側2.5パーセンタイル）をかけて、係数から引くと95%信頼区間下限値、足すと95%信頼区間上限値になる。

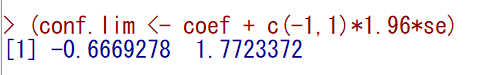
係数と信頼区間限界値をともに自然対数の肩に乗せて指数変換すると、真数のハザード比と95％信頼区間になる。

unlist(list()) を使うと、比較的きれいに表示できる。

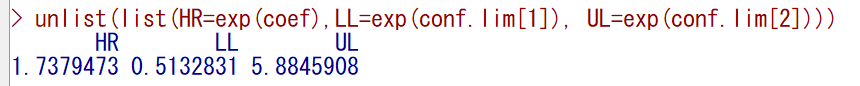
まとめ

IPTW Fine-Gray回帰を実行したい場合、EZRでは、timeregパッケージのcomp.risk()関数を使うと実行可能である。

参考になれば

EZR公式マニュアル