R で IPTW 重回帰で行ってロバスト分散を用いた信頼区間を求める方法

IPTW 重回帰を実施した後、ロバスト分散から信頼区間を求める方法

ロバスト分散信頼区間を求める必要性

IPTW（逆確率重み付け）の元となる傾向スコアの値は、真の値ではなく、推定値であるため、通常の重み付き回帰のソフトウェアが出力する分散の推定量は誤ったものになる

IPTW を重みとして用いた場合、ロバスト分散を用いた信頼区間を計算するほうが適切である

ロバスト分散は、回帰モデルが誤っている場合でも、回帰係数の妥当な分散を計算する方法である

ロバスト分散を使用することで、検定の有意水準、信頼区間の信頼係数を正しく保つことができる

IPTW 重回帰の方法

まず、IPTW を使った重回帰の方法を R スクリプトで解説する

分析を行うサンプルデータは、MASS パッケージに含まれる birthwt データセット

母親の喫煙 smoke によって、出生児の体重 bwt を予測する重回帰とする

smoke と関連する因子を用いて、傾向スコアを計算し、IPTW を作成する

# ライブラリの読み込み
library(MASS)
# データの読み込み
data(birthwt)
# 箱ひげ図
boxplot(bwt~smoke, data=birthwt)
# 平均値と標準偏差のグラフ
library(ggplot2)
ggplot(birthwt, aes(x=factor(smoke), y=bwt))+
geom_boxplot(fill=NA, color=NA)+
stat_summary(fun='mean', geom='point', size=3)+
stat_summary(fun.data='mean_sdl', fun.args=list(mult=1),
geom='errorbar', width=0.2)

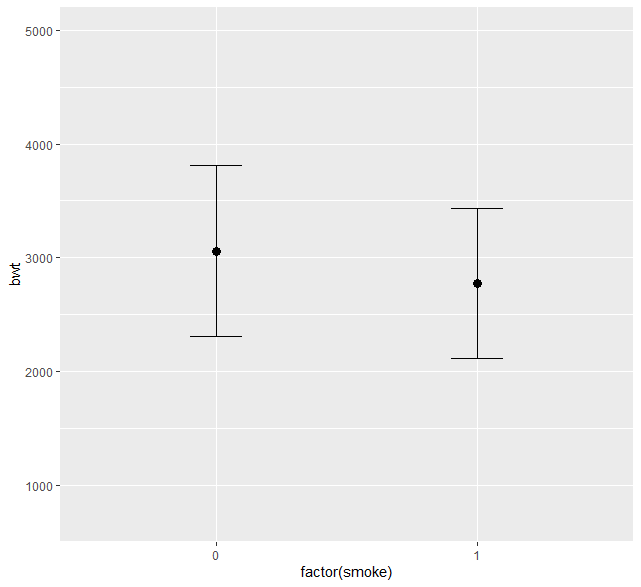
ライブラリ、データを読み込み、箱ひげ図及び平均 ± 標準偏差グラフを書いてみると以下の通り

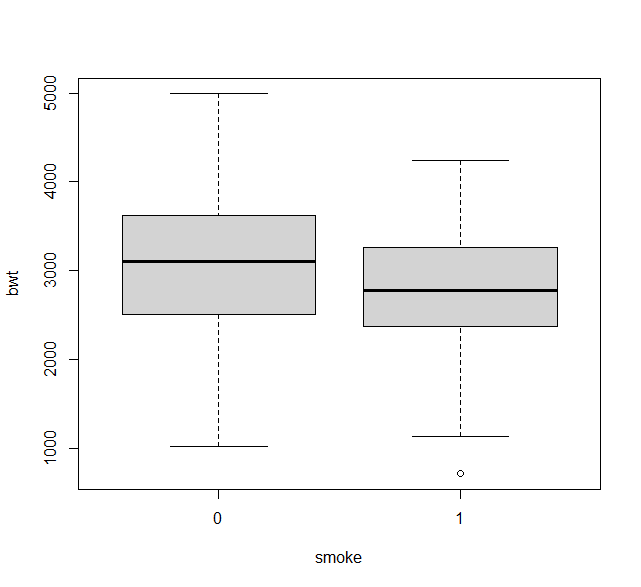
次に IPTW を計算する

# IPTWの計算
exposure <- birthwt$smoke
propensity <- glm(exposure ~ age + lwt + race + ht + ui + ftv,
family = binomial, data = birthwt)$fitted.values
weights <- ifelse(exposure, 1/propensity, 1/(1-propensity))

exposure (smoke) を、age, lwt, race, ht, ui, ftv という交絡因子候補で予測するロジスティック回帰を用いて、傾向スコア propensity を計算する

propensity を用いて、exposure =1 の場合は、propensity の逆数、exposure = 0 の場合は、1 – propensity の逆数を計算し、IPTW とする

IPTW 重回帰を実行する

# IPTW 重回帰の実行
fit <- lm(bwt ~ exposure, data = birthwt, weights = weights)
summary(fit)

bwt を exposure で説明するという回帰の際に、重み weights を指定するというスクリプトになっている

計算結果は以下の通りとなる

ロバスト分散を使用した標準誤差の計算

計算結果を利用して、sandwich パッケージの vcovHC 関数で、ロバスト分散を計算する

# ロバスト分散を使用した標準誤差の計算
library(sandwich)
se <- sqrt(diag(vcovHC(fit)))
se
estimates <- coef(fit)

計算した標準誤差はこちら

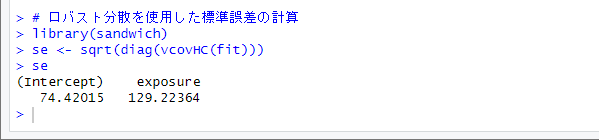
exposure の 標準誤差が、103.53 から 129.22364 と大きくなっているのがわかる

こちらのほうが妥当ということになる

ロバスト分散を使用した標準誤差を用いて、95 % 信頼区間を求める

# 95%信頼区間の計算
lower <- estimates - 1.96 * se
upper <- estimates + 1.96 * se
# 結果の出力
results <- data.frame(estimates, lower, upper)
results

結果は以下の通り

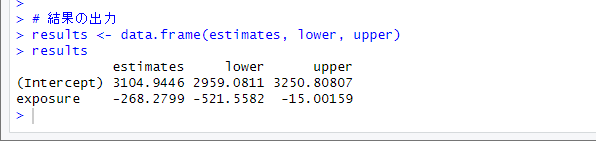
exposure の回帰係数推定値は、95 % 信頼区間の上限が 0 よりも小さく、統計学的有意である

つまり、ロバスト分散を用いた信頼区間で考えても、exposure (smoke) の影響はありそうだという結論になる

まとめ

IPTW で線形回帰を行った場合のロバスト分散信頼区間を R で求める方法を解説した

参考になれば

参考文献

交絡という不思議な現象と交絡を取りのぞく解析

参考動画

47 分 20 秒あたり