例えば、身長が高いと体重が重いとか、年齢が高いと血圧も高いとか、関係している二つの事柄は多い。
これを相関関係という。
R で、散布図、相関係数計算、相関係数検定をやってみた。
目次
相関係数を求める前に散布図を書く方法
散布図は、相関関係があるかどうかを確認する図。
相関係数を求める前には、必ず確認する必要がある。
中間テストと期末テストの点数には、相関性があるか?
見てみる。
chukan と kimatu のデータを読み込み、plot() で散布図を書く。
chukan <- c(64,40,71,33,30,71,92,23,41,55,93,74)
kimatu <- c(55,52,76,24,48,87,100,30,35,67,86,81)
plot(chukan, kimatu, xlim=c(0,100), ylim=c(0,100), pch=16, cex=1.3)
こんなふうに書ける。
中間テストの点が高いと期末テストの点も高いことが見てわかる。
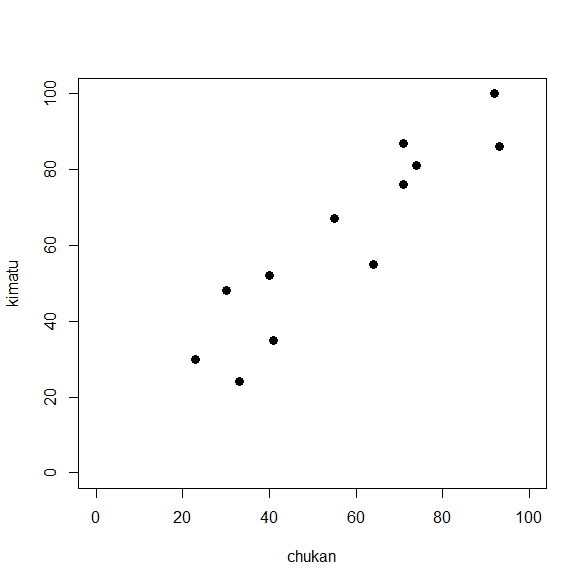
こんな感じの直線的な関係の場合は、相関係数も意味がある。
相関係数の求め方と検定の仕方
相関係数は、相関関係の強さを数字で表したもの。
1と-1が一番強い。
0が一番弱い。
1は片方が大きいときはもう片方も大きい。
-1は片方が大きいときはもう片方は小さい。
0は関係が見られない。
cor.test() で相関係数が計算できる。
cor.test(chukan, kimatu)
相関係数を計算すると、相関係数0.92の強い相関。
> cor.test(chukan, kimatu)
Pearson's product-moment correlation
data: chukan and kimatu
t = 7.3927, df = 10, p-value = 2.335e-05
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.7314858 0.9775232
sample estimates:
cor
0.9194158
母相関係数がゼロの帰無仮説は棄却。
p値は0.00002335で統計学的有意。
まとめ
二つの連続データの相関を見るのが、散布図と相関係数。
plot()で散布図が描ける。
cor.test()で相関係数の計算と検定ができる。
参考になれば。









コメント
コメント一覧 (2件)
[…] R で相関係数を計算する方法 […]
[…] R で相関係数を計算する方法 […]