疫学研究や臨床研究において、観察研究で因果推論を行う際には、治療群間の共変量バランスが取れていないことが大きな課題となる。この課題を解決するための強力な手法の一つが、IPTW (Inverse Probability of Treatment Weighting) である。IPTWを用いることで、あたかもランダム化比較試験のような状況を統計的に作り出し、治療効果のより正確な推定を目指すことができる。
IPTWを適用した後、重要なのは、ウェイトが適切に機能し、共変量のバランスが改善されたかどうかを確認することである。この確認に不可欠なのが、IPTWを適用した後のベースラインサマリー表である。本記事では、Rの tableoneパッケージを中心に、他の便利な関数も組み合わせながら、IPTW後のベースラインサマリー表を作成する方法を詳しく解説する。
IPTWの基本的な流れ(再確認)
IPTWベースラインサマリー表の作成に入る前に、IPTWの基本的な流れを簡単におさらいする。
- 傾向スコアの推定: 各参加者が特定の治療を受ける確率(傾向スコア、ここでは PS と表記する)を、ベースライン共変量を用いてロジスティック回帰などで推定する。
- ウェイトの計算: 推定された傾向スコアに基づいて、各参加者のウェイトを計算する。一般的なのは、ATT (Average Treatment effect on the Treated) または ATE (Average Treatment effect) のウェイトである。
- ATTの場合:
- 治療群: $w_i = 1$
- 対照群: $w_i = \frac{\text{PS}_i}{1 – \text{PS}_i}$
- ATEの場合:
- 治療群: $w_i = \frac{1}{\text{PS}_i}$
- 対照群: $w_i = \frac{1}{1 – \text{PS}_i}$
- ATTの場合:
- ウェイトの適用: 計算されたウェイトをデータに適用し、ウェイト付きの統計解析を行う。
本記事では、既にウェイトがデータセットに追加されていることを前提に進める。
使用するRパッケージ
今回使用する主なRパッケージは以下の通りである。事前にインストールしておくこと。
#install.packages(c("dplyr", "tableone", "survey", "ggplot2", "cobalt"))
library(dplyr)
library(tableone)
library(survey)
library(ggplot2)
library(cobalt) # バランスチェックのために非常に便利サンプルデータの準備
架空のデータセットを作成し、IPTWのウェイトを追加する。
# 乱数シードの設定
set.seed(123)
# サンプルデータの作成
n <- 500 # サンプルサイズ
data_df <- tibble(
id = 1:n,
treatment = sample(c(0, 1), n, replace = TRUE, prob = c(0.6, 0.4)), # 治療群 (0:対照, 1:治療)
age = round(rnorm(n, 50, 10)), # 年齢
sex = sample(c("Male", "Female"), n, replace = TRUE, prob = c(0.5, 0.5)), # 性別
bmi = round(rnorm(n, 25, 5),1), # BMI
comorbidity = rbinom(n, 1, 0.3) # 併存疾患 (0:なし, 1:あり)
)
# 傾向スコアの推定 (ここでは簡易的なロジスティック回帰)
ps_model <- glm(treatment ~ age + sex + bmi + comorbidity, data = data_df, family = binomial())
data_df$prop_score <- predict(ps_model, type = "response")
# ATEウェイトの計算
data_df <- data_df %>%
mutate(
iptw_weight = ifelse(treatment == 1, 1 / prop_score, 1 / (1 - prop_score))
)
# ウェイトのトリミング (オプションだが推奨)
# 極端なウェイトは不安定性をもたらすため、トリミングは重要である。
# 例えば、上位・下位1%をトリミング
quantile_trim_lower <- quantile(data_df$iptw_weight, 0.01)
quantile_trim_upper <- quantile(data_df$iptw_weight, 0.99)
data_df <- data_df %>%
mutate(
iptw_weight_trimmed = pmin(pmax(iptw_weight, quantile_trim_lower), quantile_trim_upper)
)
# 以降、iptw_weight_trimmed を使用tableone を使ったベースラインサマリー表の作成
tableone パッケージは、非常に簡単にベースラインの患者特性表(Table 1)を作成できることで知られている。ウェイトを考慮した表を作成するには、svyglmなどと同じようにsurveyパッケージのsvydesignオブジェクトを使用する。
ウェイトなしのベースラインサマリー表(比較用)
まず、ウェイトを考慮しない通常のベースラインサマリー表を作成し、ウェイト適用後の表と比較できるようにする。
# ベースライン共変量のリスト
myVars <- c("age", "sex", "bmi", "comorbidity")
# カテゴリカル変数のリスト
catVars <- c("sex", "comorbidity")
# ウェイトなしのTableOne
table1_unweighted <- CreateTableOne(
vars = myVars,
strata = "treatment",
data = data_df,
factorVars = catVars
)
# 表の表示
print(table1_unweighted, smd = TRUE) # SMD (Standardized Mean Difference) も表示実行結果:
> # 表の表示
> print(table1_unweighted, smd = TRUE) # SMD (Standardized Mean Difference) も表示
Stratified by treatment
0 1 p test SMD
n 305 195
age (mean (SD)) 49.65 (10.13) 51.09 (9.91) 0.118 0.144
sex = Male (%) 152 (49.8) 96 (49.2) 0.968 0.012
bmi (mean (SD)) 25.06 (4.87) 25.25 (5.11) 0.676 0.038
comorbidity = 1 (%) 91 (29.8) 56 (28.7) 0.867 0.025ここでsmd = TRUEとすることで、標準化平均差 (Standardized Mean Difference; SMD) が表示される。SMDは、各共変量が治療群と対照群でどれだけバランスが取れているかを示す指標であり、一般的に0.1以下であれば良好なバランスと判断される。こちらのウェイトなしの表では、age が SMD 0.1 以上でバランス不良である。
IPTWウェイトを考慮したベースラインサマリー表
次に、IPTWウェイトを考慮したベースラインサマリー表を作成する。これには、surveyパッケージのsvydesign関数でデザインオブジェクトを作成し、それをCreateTableOneに渡す必要がある。
# surveyパッケージのデザインオブジェクトを作成
# id = ~1 はクラスタリングがないことを示す
# weights = ~iptw_weight_trimmed でウェイトを指定
svy_design <- svydesign(
id = ~1,
weights = ~iptw_weight_trimmed,
data = data_df
)
# surveyパッケージのデザインオブジェクトからTableOneを作成
# svyCreateTableOne関数を使用
table1_weighted <- svyCreateTableOne(
vars = myVars,
strata = "treatment",
data = svy_design, # svydesignオブジェクトをdata引数として渡す
factorVars = catVars
)
# 表の表示
print(table1_weighted, smd = TRUE)実行結果:
> # 表の表示
> print(table1_weighted, smd = TRUE)
Stratified by treatment
0 1 p test SMD
n 500.13 499.93
age (mean (SD)) 50.21 (10.15) 50.21 (10.08) 1.000 <0.001
sex = Male (%) 249.5 (49.9) 251.6 (50.3) 0.924 0.009
bmi (mean (SD)) 25.12 (4.87) 25.12 (5.12) 0.996 <0.001
comorbidity = 1 (%) 147.6 (29.5) 148.1 (29.6) 0.979 0.002
> このウェイト付きの表では、age を含む全共変量のSMDがウェイトなしの表と比較して大幅に減少していることを確認できる。これは、IPTWが共変量のバランスを改善する上で効果的に機能していることを示している。
その他のバランスチェック関数 (cobaltパッケージ)
tableone は素晴らしいが、視覚的なバランスチェックにはcobaltパッケージのbal.plotやlove.plotが非常に便利である。
SMDのLove Plot
SMDのLove Plotは、各共変量のSMDを視覚的に比較するのに役立つ。ウェイト適用前と適用後の両方をプロットすることで、バランス改善の効果が一目でわかる。
# ウェイト適用前後のバランスを計算
# treat: 治療群変数, covs: 共変量リスト
# weights: ウェイト変数 (なしの場合はunweighted)
bal_results <- bal.tab(
treatment ~ age + sex + bmi + comorbidity,
data = data_df,
estimand = "ATE", # ATEウェイトの場合
weights = "iptw_weight_trimmed",
method = "weighting",
un = TRUE,
disp.means = TRUE,
disp.v.ratio = TRUE # SMDを表示
)
# Love PlotをPNGファイルに出力
png("IPTW_summary_table_love_plot.png", width = 1000, height = 800, res = 120)
love.plot(
bal_results,
stats = "mean.diffs", # SMDを表示
threshold = 0.1, # 閾値を設定
var.order = "alphabetical", # 変数をアルファベット順に並べ替え
stars = "raw",
title = "Love Plot of Covariate Balance Before and After IPTW"
)
dev.off()実行結果:
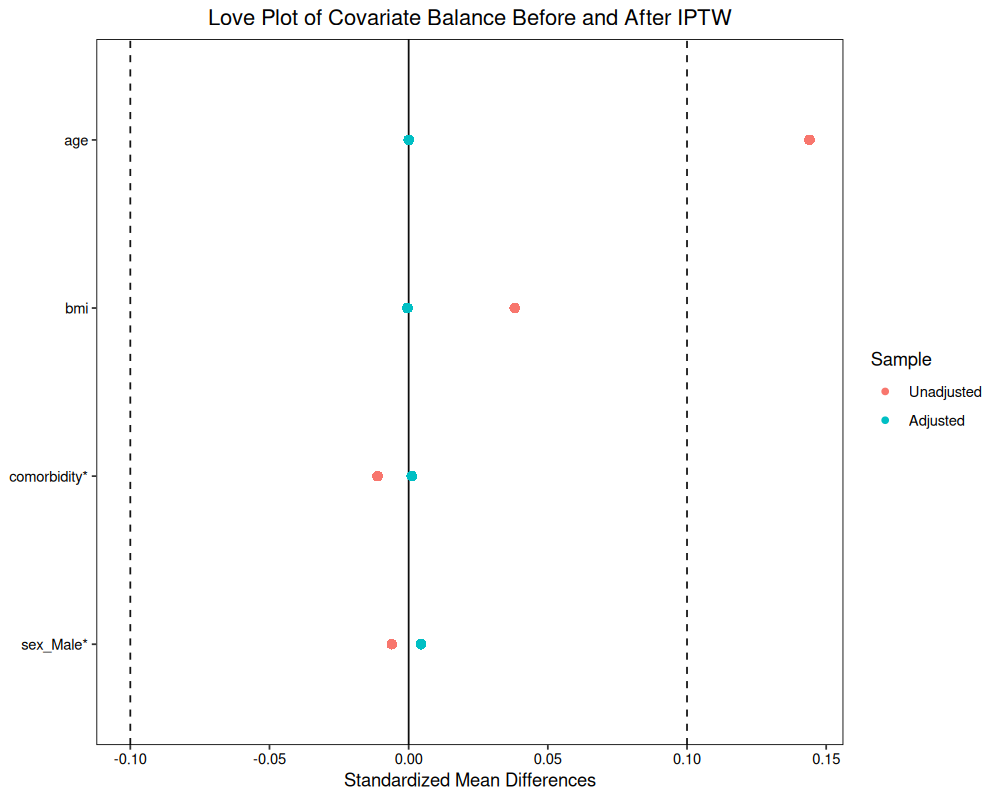
このプロットでは、各共変量のSMDがウェイト適用前(”Unadjusted”)と適用後(”Adjusted”)でどのように変化したかが示される。理想的には、Adjusted の全ての点のSMDが閾値(例えば0.1)以下に収まっていることが望ましい。このグラフは、水色の点が、-0.1 から +0.1 に収まっているので、理想的である。
傾向スコアの分布
傾向スコアの分布を治療群ごとに可視化することも重要である。ウェイト適用後、傾向スコアの分布がより重なるようになっているかを確認する。
# 傾向スコアの分布(ウェイトなし)
ggplot(data_df, aes(x = prop_score, fill = factor(treatment))) +
geom_density(alpha = 0.6) +
labs(title = "Propensity Score Distribution (Unweighted)",
x = "Propensity Score",
y = "Density",
fill = "Treatment") +
theme_minimal()
ggsave("IPTW_summary_table_propensity_score_distribution_unweighted.png", width = 8, height = 6)
# 傾向スコアの分布(ウェイト付き)
# surveyパッケージのsvyhistなどを使うか、手動でウェイトを適用したヒストグラムを作成
# ggplot2のaesにweightを指定することで、ウェイト付きのプロットが可能
ggplot(data_df, aes(x = prop_score, fill = factor(treatment), weight = iptw_weight_trimmed)) +
geom_density(alpha = 0.6) +
labs(title = "Propensity Score Distribution (IPTW Weighted)",
x = "Propensity Score",
y = "Weighted Density",
fill = "Treatment") +
theme_minimal()
ggsave("IPTW_summary_table_propensity_score_distribution_weighted.png", width = 8, height = 6)
実行結果:
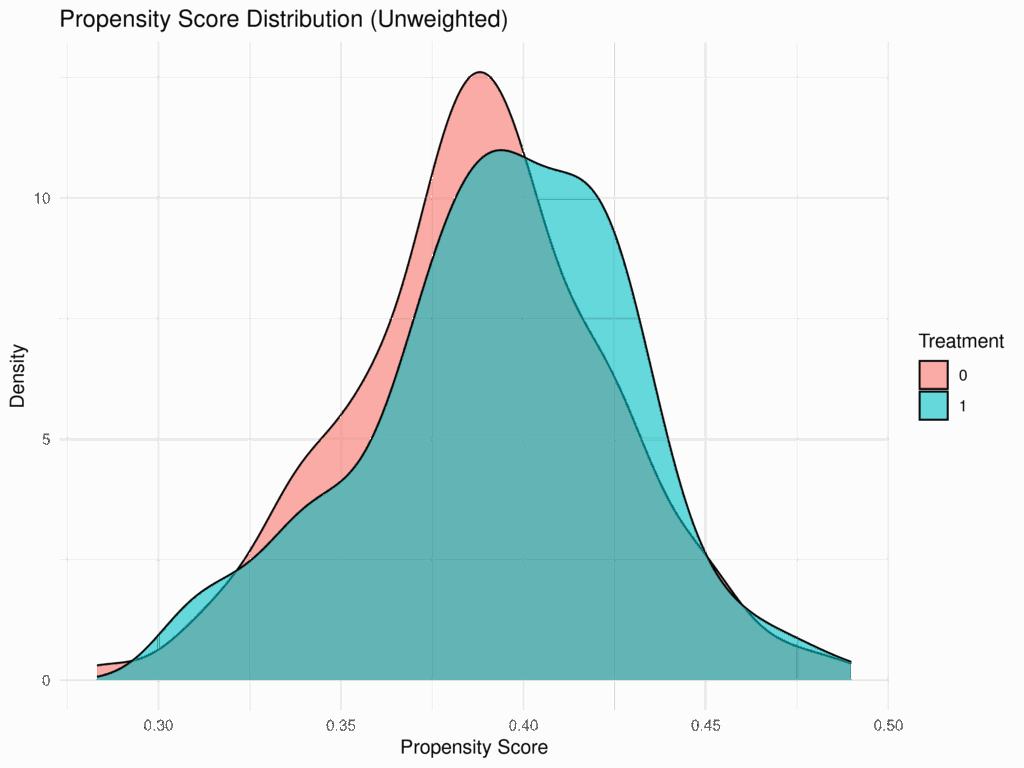
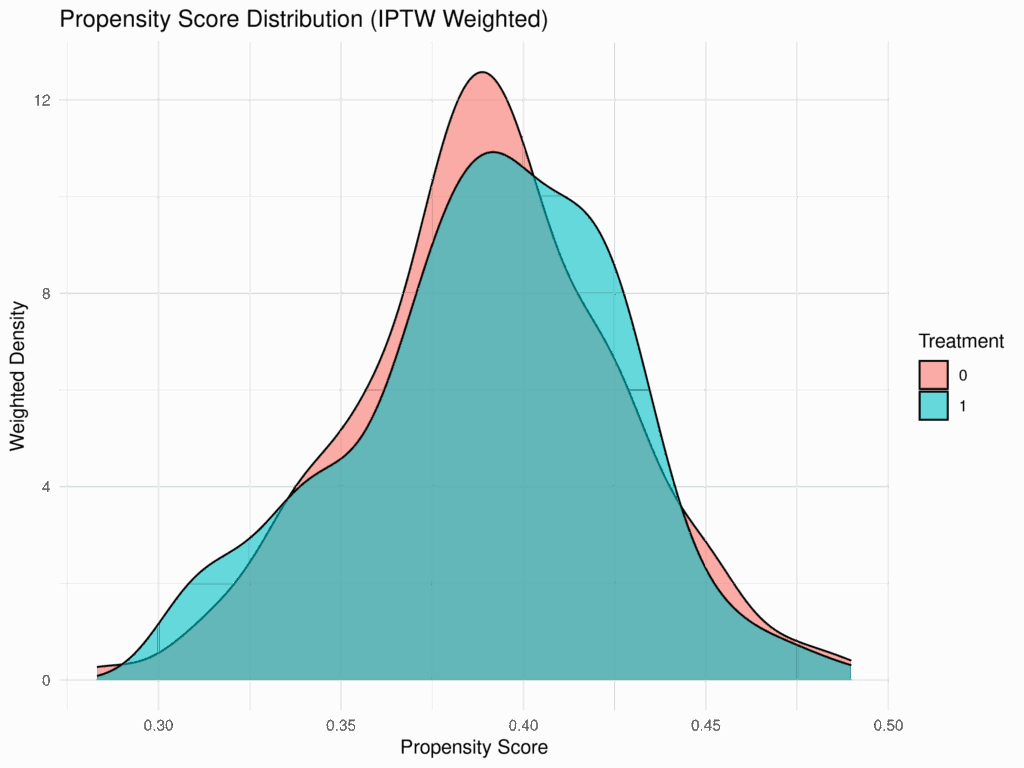
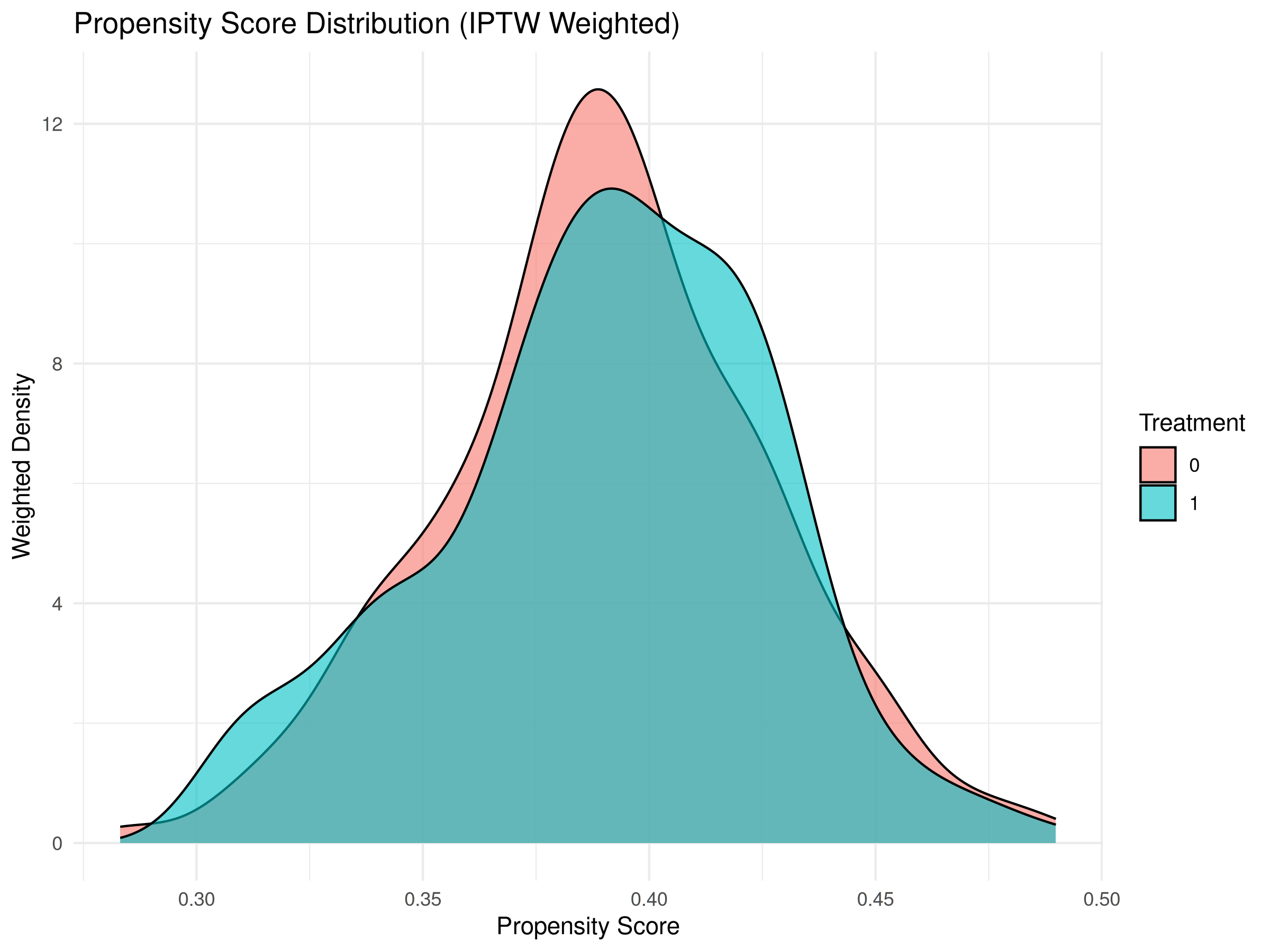
ウェイト適用後(IPTW Weighted)のプロットでは、治療群と対照群の傾向スコアの分布が、ウェイトなしの場合よりも類似していることを確認できる。これは、IPTWがオーバーラップを改善し、バランスを調整している証拠である。
まとめ
本記事では、Rの tableone パッケージを中心に、IPTWベースラインサマリー表の作成方法を解説した。surveyパッケージと組み合わせることで、簡単にウェイトを考慮した表を作成できる。
また、cobaltパッケージを用いたLove Plotや傾向スコアの分布の可視化は、IPTWによるバランス改善の効果を視覚的に確認する上で非常に有用である。これらのツールを使いこなすことで、より信頼性の高い因果推論に繋がるであろう。
IPTWは強力なツールであるが、適切なウェイトの計算、トリミング、そしてバランスチェックが不可欠である。これらの手順を丁寧に行い、研究の質を高めていくことを推奨する。





コメント