統計モデリングを行う際、データの「分散」が均一であるという仮定を置くことがよくある。しかし、現実のデータではこの仮定が成り立たない、つまり「不均一分散」を示すケースが少なくない。不均一分散は、統計的推論の信頼性を損なう可能性があり、適切な対処が不可欠である。本記事では、不均一分散とは何か、その問題点、そして様々な対処法について、具体的な例を交えながら解説する。特に、統計解析ツールRを用いた計算例も紹介し、実践的な理解を深めていく。
不均一分散とは
不均一分散(Heteroscedasticity)とは、統計モデルにおける誤差項の分散が、説明変数の値によって異なる状態を指す。例えば、ある説明変数の値が小さいときには誤差のばらつきが小さいのに、その値が大きくなるにつれて誤差のばらつきも大きくなる、といった状況が不均一分散の典型例である。これに対し、誤差項の分散が説明変数の値にかかわらず一定である状態を均一分散(Homoscedasticity)と呼ぶ。
不均一分散の問題点
不均一分散が存在する場合、最小二乗法(OLS)を用いた線形回帰モデルの推定結果には、以下のような問題が生じる。
- 係数推定量の不偏性は保たれるが、効率性が失われる: 推定された回帰係数は正しい値を指すものの、その推定値のばらつきが大きくなる。
- 標準誤差の過小評価または過大評価: 不均一分散がある場合、OLSが算出する標準誤差は真の標準誤差を正確に反映しない。多くの場合、標準誤差が過小評価され、結果として統計的有意性があるという誤った結論を導きやすくなる。
- 信頼区間と仮説検定の信頼性の低下: 標準誤差の不正確さにより、構築される信頼区間は真の母数をカバーせず、仮説検定の結果も信頼できなくなる。これにより、誤った意思決定につながる可能性がある。
不均一分散の対処法
不均一分散に対処するための方法はいくつか存在する。
- 頑健な(ロバスト)標準誤差(Robust Standard Errors)の使用:不均一分散が存在しても、回帰係数の推定値自体は不偏性を保つ。問題は標準誤差の不正確さにあるため、これを補正する方法である。Whiteの頑健標準誤差(またはHuber-White標準誤差)が代表的であり、これは不均一分散が存在しても、漸近的に正しい標準誤差を与えることが知られている。Rでは
sandwichパッケージなどを用いて簡単に計算できる。 - 分散安定化変換(Variance Stabilizing Transformation):従属変数に数学的な変換を施すことで、誤差の分散を均一に近づける方法である。
- 対数変換(Log Transformation): データが広範囲に分布し、分散が平均値に比例して大きくなる場合に有効である。例:$Y’=\log{Y}$
- 平方根変換(Square Root Transformation): ポアソン分布に従うカウントデータなど、分散が平均値に比例する場合に有効である。例:$Y’=\sqrt{Y}$
- 逆数変換(Reciprocal Transformation): 分散が平均値の2乗に比例する場合などに有効である。例:$Y’=1/Y$ ただし、変換後のモデルの解釈が元の尺度と異なるため、注意が必要である。
- 加重最小二乗法(Weighted Least Squares, WLS):誤差の分散が小さい観測値には大きな重みを、分散が大きい観測値には小さな重みを与えて回帰分析を行う方法である。分散の逆数を重みとして使用する。分散の構造を事前に知る必要があるため、適用が難しい場合もあるが、不均一分散のパターンが特定できる場合には非常に有効である。
- 一般化線形モデル(Generalized Linear Models, GLMs):ポアソン回帰(カウントデータ)、ガンマ回帰(連続で正の値を取るデータ)など、誤差の分布が正規分布ではないデータに対応するモデルである。これらのモデルでは、平均と分散の関係をモデル内に組み込むことができるため、不均一分散の問題をより自然に扱うことができる。
不均一分散の具体例
例えば、ある企業の売上データと広告費の関係を分析するケースを考える。広告費が少ない小規模な企業では売上のばらつきも小さいかもしれないが、広告費を莫大に投じる大企業では売上のばらつきも非常に大きくなる可能性がある。これは、広告費が増えるにつれて売上の予測誤差(残差)のばらつきが大きくなる、典型的な不均一分散の例である。
Rでの計算例
ここでは、不均一分散を持つダミーデータを作成し、OLS回帰と頑健標準誤差を用いたOLS回帰の結果を比較するRでの計算例を示す。
# 必要なパッケージをインストール(まだインストールしていない場合)
# install.packages("lmtest")
# install.packages("sandwich")
# パッケージの読み込み
library(lmtest) # coeftest関数用
library(sandwich) # vcovHC関数用
# 不均一分散を持つダミーデータの生成
set.seed(123)
n <- 100
x <- runif(n, 1, 10) # 説明変数
# 誤差の分散がxの増加とともに大きくなるように設定
epsilon <- rnorm(n, 0, 0.5 * x)
y <- 2 + 3 * x + epsilon # 従属変数
# データをデータフレームにまとめる
df <- data.frame(x, y)
# データの可視化(不均一分散の確認)
par(mfrow = c(2,1), mar = c(5,5,3,2), oma = c(0,0,0,0), cex = 1.5)
plot(df$x, df$y,
main = "不均一分散を持つデータの例",
xlab = "説明変数 (x)",
ylab = "従属変数 (y)")
# 回帰直線を追加
abline(lm(y ~ x, data = df), col = "red")
# OLS回帰モデルの推定
model_ols <- lm(y ~ x, data = df)
summary(model_ols)
# OLSモデルの残差プロット
plot(model_ols$fitted.values, model_ols$residuals,
main = "OLSモデルの残差プロット",
xlab = "予測値",
ylab = "残差")
abline(h = 0, col = "red", lty = 2) # ゼロライン
# 頑健標準誤差を用いた係数推定
# type = "HC1"はWhiteの頑健標準誤差の一種
coeftest(model_ols, vcov = vcovHC(model_ols, type = "HC1"))
実行結果:
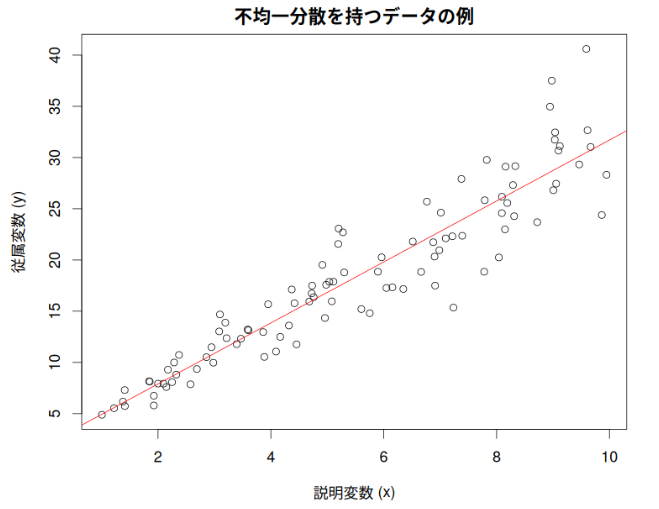
説明変数 x が大きいほど、従属変数 y のばらつきが大きいのがわかる
> # OLS回帰モデルの推定
> model_ols <- lm(y ~ x, data = df)
> summary(model_ols)
Call:
lm(formula = y ~ x, data = df)
Residuals:
Min 1Q Median 3Q Max
-8.1305 -1.6273 0.0422 1.2916 10.1121
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.9557 0.6977 2.803 0.0061 **
x 2.9753 0.1153 25.805 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.943 on 98 degrees of freedom
Multiple R-squared: 0.8717, Adjusted R-squared: 0.8704
F-statistic: 665.9 on 1 and 98 DF, p-value: < 2.2e-16
> 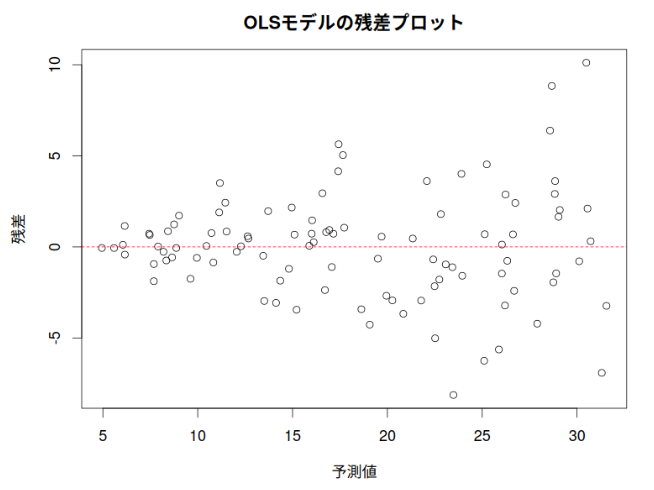
予測値が大きいと、残差のばらつきが大きいことがわかる
> # 頑健標準誤差を用いた係数推定
> # type = "HC1"はWhiteの頑健標準誤差の一種
> coeftest(model_ols, vcov = vcovHC(model_ols, type = "HC1"))
t test of coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.95569 0.52698 3.7111 0.0003426 ***
x 2.97528 0.12584 23.6426 < 2.2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
> 結果解釈
上記のRのコードを実行すると、まず通常のsummary(model_ols)の結果が表示される。この結果では、係数の推定値とその標準誤差、p値、信頼区間が示される。不均一分散が存在する場合、ここで表示される標準誤差は過小評価されている可能性がある。
また、残差プロットでは、予測値が大きくなるにつれて残差のばらつきも大きくなる「漏斗型」のパターンが観察されれば、不均一分散が存在することを示唆する。
最後に、coeftest(model_ols, vcov = vcovHC(model_ols, type = "HC1"))の結果を見てほしい。これは頑健標準誤差を用いて再計算された標準誤差に基づいた係数の検定結果である。通常、この頑健標準誤差はOLSの標準誤差よりも大きくなる傾向がある。今回の例も、0.1153 だった標準誤差が、頑健標準誤差では、0.12584 と少しだけ大きくなっている。その結果、t値が小さくなり、p値が大きくなることで、OLSでは統計的に有意と判断されていた係数が、頑健標準誤差を用いると有意ではなくなることがある。この頑健標準誤差を使うことは、より信頼性の高い統計的推論を意味する。
まとめ
不均一分散は、統計モデリングにおいて見過ごされがちな問題であるが、その影響は統計的推論の信頼性を大きく損なう可能性がある。本記事で紹介したように、頑健な標準誤差の使用、データ変換、加重最小二乗法、そして一般化線形モデルの適用など、様々な対処法が存在する。
データの性質や分析の目的に応じて適切な対処法を選択し、より頑健で信頼性の高い統計的分析を行うことが、データに基づいた意思決定の精度向上に繋がる。分析を行う際には、残差プロットなどで不均一分散の兆候がないかを確認し、必要に応じて適切な対処を行う習慣をつけよう。




コメント