多重代入法で必要な補完データセット数

2022年1月29日2024年10月1日

欠測値があった場合、対処する方法がいくつかある。

そのうちの一つが多重代入法である。

多重代入法で作成すべき欠測値補完データの数はいくつがよいのか？

＞＞もう統計で悩むのは終わりにしませんか？

↑期間・数量限定で無料プレゼント中！

多重代入法で作成するデータセットはいくつがよいと言われているか？

多重代入法の提案者Rubinは、5 から 10 程度で解析可能と主張して、その後 5 つ程度で実際行われてきた。

Rubinが提唱したのは1987年で、その当時と比べるとコンピュータは格段に進化し、現在は 100 程度のデータを作成するのは大した労力がかからない。

実際、100 個のデータを作成することも勧められている。

多重代入法で作成するデータセット数を決める方法は？

多重代入法で作成するデータセットの数を決める方法の一つに、相対効率（Relative Efficiency）で決めるという方法がある。

母集団での欠測情報の割合を $ \lambda_0 $ とすると、欠測値補完データセット D と相対効率 $ Re_D $ の間には、以下の関係が成り立つ。

$$ Re_D = \left( 1 + \frac{\lambda_0}{D} \right)^{-1} $$

ここで母集団での欠測情報の割合 $ \lambda_0 $ は、単変量で完全にランダムな欠測の場合は、欠測率にあたる。

相対効率は高いほうが良い。

＞＞もう統計で悩むのは終わりにしませんか？

↑1万人以上の医療従事者が購読中

相対効率を用いて欠測情報割合とデータセット数のシミュレーションを行う

相対効率を指標にして、欠測情報の割合と欠測値補完のデータセット数を割り当てたときのシミュレーションを行ってみた。

欠測情報割合は 10 ％（0.1）ごとに 0.1 から 1 までとした。

1 というのはすべて欠測情報であることを意味するのでありえないが、理屈の上では計算できるため含めた。

データセット数は、5, 10, 20, 50, 100, 200 とした。

これらのデータセット数は、よく見かける情報を参考に選んだ。

以下に、これらの条件で、マトリックス状に計算結果を出力する R のスクリプトを示す。

lambda0 <- 1:10/10
D <- c(5,10,20,50,100,200)
res.tab <- matrix(rep(0,60),nr=6)
for (i in 1:length(D)){
for (j in 1:length(lambda0)){
ReD <- 1/(1+lambda0[j]/D[i])
res.tab[i,j] <- ReD
}
}
colnames(res.tab) <- lambda0
rownames(res.tab) <- D
res.tab

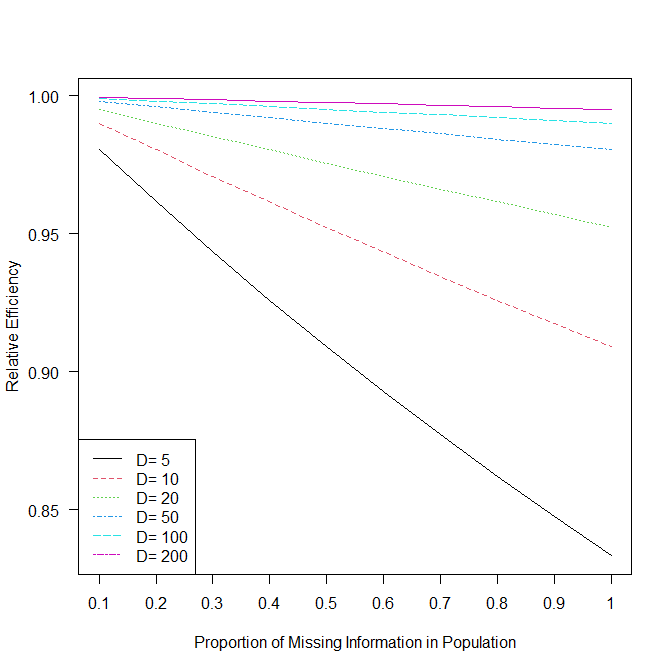
計算結果 res.tab（出力は省略している）をmatplot()関数を使ってグラフ化すると以下の通りになる。

どのデータセット数であっても、欠測情報の割合が大きくなると、相対効率は低くなる。

100 と 200 の差はわずかであることがわかる。

つまり、100 個作成すれば、まず間違いないということになる。

matplot(t(res.tab),type="l",xaxt="n",ylab="Relative Efficiency",las=1,
xlab="Proportion of Missing Information in Population")
axis(1, at=1:10, formatC(1:10/10))
legend(legend=paste("D=",D),"bottomleft", lty=1:5, col=1:6)