前後2時点の対応のあるデータを群間比較するときは、共分散分析を使う
EZR と SPSS の方法を解説
対応のあるデータの群間比較の考え方
対応のあるデータの群間比較の際に、考え方が2つある。
一つは、後のデータを目的変数に、群別変数を着目する説明変数に、前のデータを共変量にする方法。
群別変数も共変量も、ともに説明変数である。
もう一つは、前後の差のデータを目的変数に、群別変数を着目する説明変数に、前のデータを共変量にする方法。
後のデータや、前後の差のデータを群間比較するだけだと、前のデータの群間における偏りが考慮できない。
そんなときに、共分散分析を使うと、前のデータを考慮に入れながら、群間比較できるわけだ。
EZRで実際にやってみる
EZR公式マニュアルのデータを使って、対応のあるデータで群間比較を行ってみる。
データは、CDratio1, CDratio2が対応のあるデータ、AGVHD24が群別変数とする。
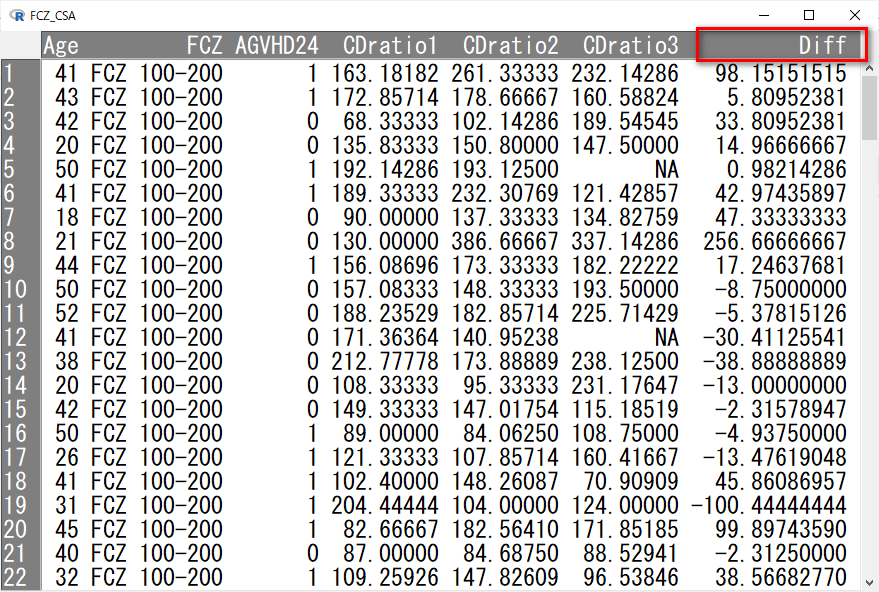
CDratio1とCDratio2の差は、Diff という名前であらかじめ作成しておく。
後の測定値を目的変数にする場合
「統計解析」→「連続変数の解析」→「共分散分析」を選択する。
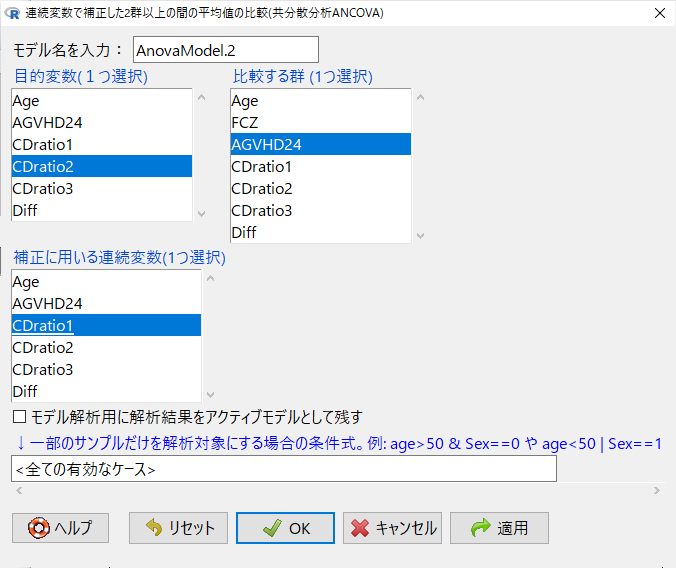
目的変数にCDratio2, 比較する群にAGVHD24, 補正に用いる連続変数にCDratio1とする。
これでOKをクリックすると解析結果が出力される。
まず、群別変数と共変量の間の交互作用の検討が行われる。
有意水準を5%とすれば、交互作用があるとは言えないということになり、解析を群別に分けなくてもよいという判断になる。

CDratio1で調整した、AGVHD24の2群の分散分析という形になる。

有意水準を5%とすれば、AGVHD24は統計学的有意ではなく、群間差はないという結果になる。
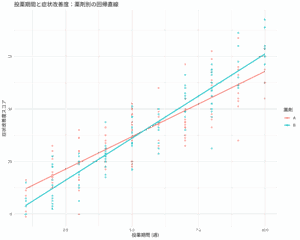
グラフが同時に出力されており、青 (AGVDH24=0) の回帰直線とピンク (AGVHD24=1) の回帰直線がほぼ同じであることがわかり、ここからも、2群が異ならないことがわかる。
前後差を目的変数にする場合
前後差を目的変数にする場合は、先ほど CDratio2 とした目的変数を Diff に変える。
交互作用と群別変数のp値は、ともに先ほどと同じ結果になる。

なので、目的変数に後のデータを使うか、前後の差を使うかに、本質的には違いがないと言える。
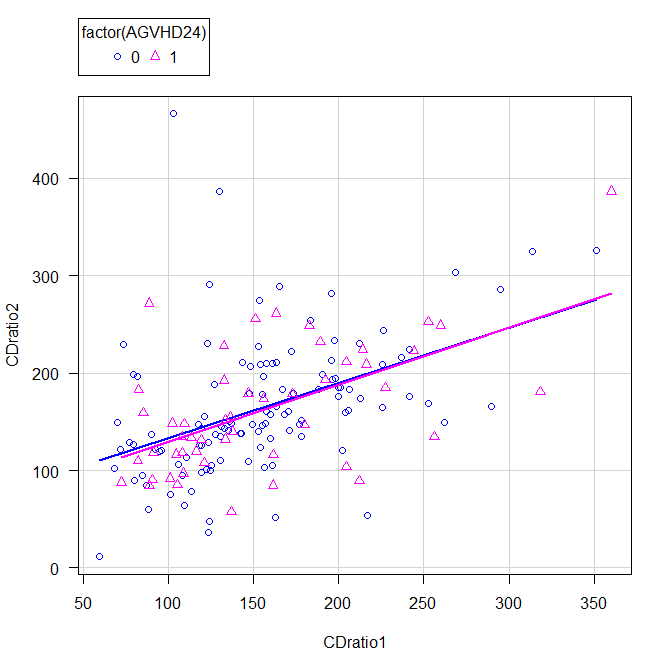
グラフは、先ほどとは異なり、右肩下がりになった。
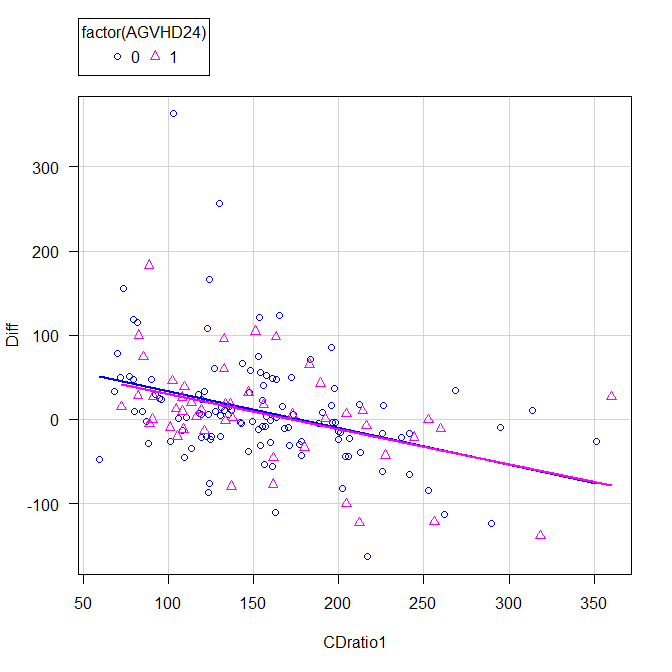
これは、CDratio1が大きいほど、変化量は小さいという関係性が示されている。
しかしながら、群間には違いがないのは先ほどと同じである。
EZRで重回帰式のパラメータを推定する方法
共分散分析のメニューを使うと、重回帰式のパラメータを推定することができない。
回帰直線の傾きや切片が知りたい場合は、「統計解析」→「連続変数の解析」→「重回帰」を選択する。
目的変数には、CDratio2かDiffを入れる。
説明変数にはAGVHD24とCDratio1を入れる。
Controlキーを押しながらクリックすると複数選択できる。
OKを押すと、解析結果が出力される。
以下の部分のCDratio1の回帰係数推定値が傾きである。

AGVHD24の数値は、1のグループでは、回帰係数推定値分だけ足される。
今回の場合は係数がマイナスなので、引かれる形になる。
この場合は、傾きは平行であることを前提としていて、AGVHD24の回帰係数推定値分がY軸方向に水平移動になる。
前後差を目的変数にすると、以下のような結果になる。

ちなみに、重回帰分析であっても、共分散分析であっても、p値は同じなので、どちらを使っても本質的には同じでどちらでもよいことがわかる。
SPSS で共分散分析を行う方法
一般線型モデルメニューを使う場合
前後差を目的変数にした方法を実行してみる。
まずは一般線型モデルのメニューを使う。
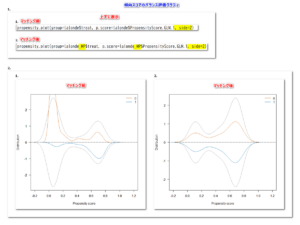
以下のように従属変数にDiff、固定因子にAGVHD24、共変量にCDratio1を投入する。
オプションをクリックし、パラメータ推定値にチェックを入れる。
これで分散分析の結果だけでなく、パラメータ推定を出力してくれる。
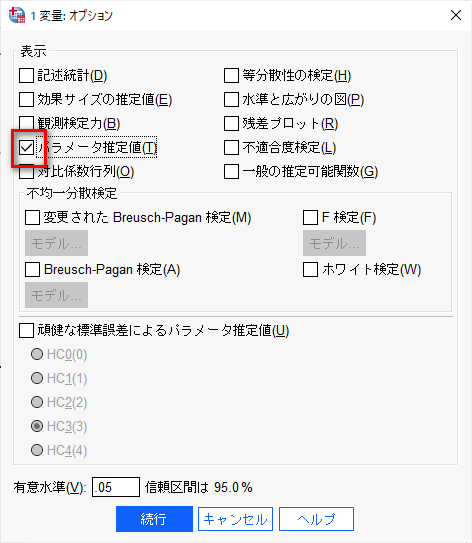
続行をクリックして、OKをクリック。
パラメータ推定値の表がメインの表である。
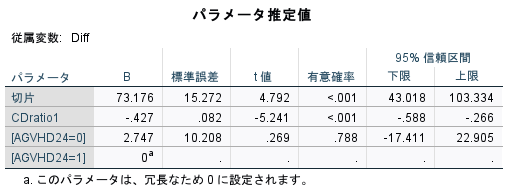
AGVHD24の有意確率は、上記のものと同じだが、推定値Bは、-がついておらず符号が逆である。
これは、AGVHD24=1が参照カテゴリになっているためである。
一般線型モデルのメニューはこれを自由に指定できない。
逆にしたい場合は、変数の0と1を逆にしておく必要がある。
回帰 → 線型 メニューを使う場合
次に、回帰→線型のメニューを使ってみる。
従属変数にDiff、独立変数にAGVHD24とCDratio1を投入する。
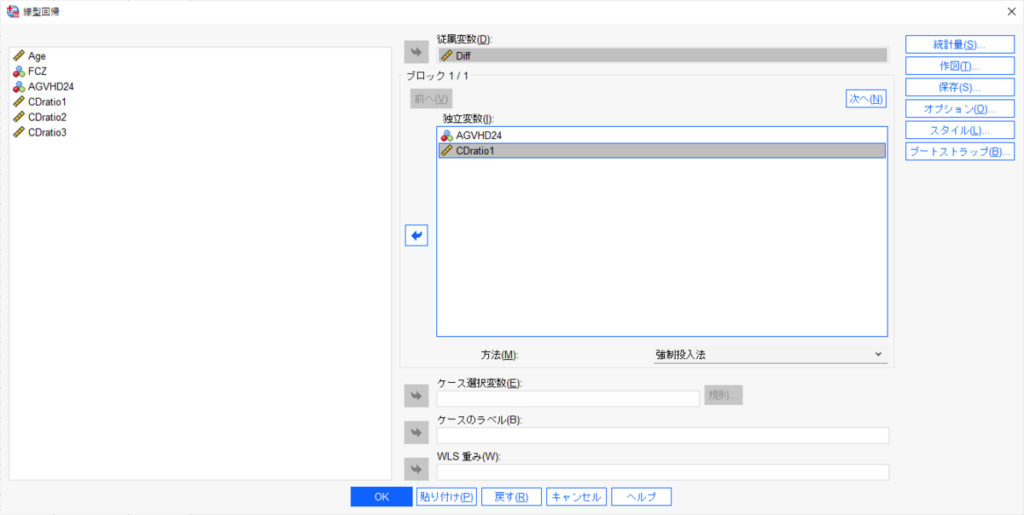
OKをクリックすると結果が出力される。
係数というタイトルの表がメインの結果表である。
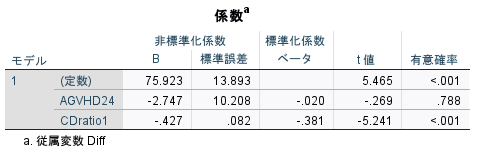
今度は、AGVHD24の有意確率のみならず、Bの値も符号を含めてEZRの結果と同じになる。
このとき、AGVHD24=0が参照カテゴリになって、1のときに-2.747という意味である。
これのほうがわかりやすい。
だが、回帰→線型のメニューは、1/0のデータはこれでよいが、3群以上のカテゴリの際にはダミー変数を作成して、適切に投入しないといけない。
これがややこしい点である。
慣れれば大したことないが、ダミー変数とは何か?
なぜカテゴリカルデータの1,2,3をそのまま入れてはダメなのか?
を理解する必要があるので、SPSSのこのメニューはハードルが高く使いづらい。
このような一長一短はあるにせよ、SPSSでも対応のあるデータの群間比較を共分散分析で解析することができる。
ちなみに、共分散分析は、一般線型 (線形でも同じ) モデルとも呼べるし、カテゴリカルデータをダミー変数にして投入した重回帰分析とも言える。
まとめ
対応のあるデータの群間比較を共分散分析で解析する方法を紹介した。
後のデータか、前後の差のデータの解析したいほう (多くの場合は変化量を問題にしたいのではなかろうか?その場合は差を用いるとよい) を目的変数として、群別変数と前のデータを説明変数とする。
EZRで分散分析の結果だけでよければ、共分散分析のメニューを使う。
傾きや切片の推定を行いたければ、重回帰のメニューを使う。
SPSSでは、一般線型モデルか、回帰→線型メニューを使えば実行可能。
対応のあるデータを群間比較したいが、対応のあるt検定では群間比較できない!どうしたらいい??ってなったときに、この方法を使うと解決する。
参考書籍
EZR公式マニュアル








コメント