多重共線性(たじゅうきょうせんせい)があるかどうかを確認する必要があるとはよく聞くが、確認して多重共線性があった場合はどうすればよいのか?
多重共線性とは?多重共線性はなぜ問題なのか?そして多重共線性を回避するにはどうすればよいか?についてまとめた。
多重共線性とは?
回帰分析は、変数Xで変数Yを予測する式を作ることが目的だ。重回帰分析は変数Xが二つ以上の式を予測する。
変数Yを決める要因は色々あるはず。例えば、体重 Y は、身長と一番相関するが、当然食べる量に関係する。食べる量だけじゃなく、運動量も、筋肉量も、年齢も関係するはずだ。
いろいろな要因で体重を予測する式を作るのが重回帰分析。予測式ができれば、どれだけ食べたらどれだけ太るか予測できる。また、どれだけ動かないと、どれだけ太るか予測できる。
いろいろ体重に関係してそうな要因を選んでいくと、とても似ている要因が出てくる。
例えば、体重には、運動量も関係するし、筋肉量も関係する。そして、筋肉量と運動量がとても関係がある。運動量が多いと筋肉量も多い。運動量が少ないと筋肉量も少ない。この関係がとても強い場合、同時に考えることができない。
仮に、運動量と筋肉量が相関係数0.9だったとする。「とても強い関係」とは、相関係数0.9というようなレベル。相関係数1が最高なので、0.9はかなりのハイレベル。こんなときは同時に考えると数式が ”パンク” する。
予測式を作りたいいくつかの説明変数同士の相関係数が0.9などと高い場合、多重共線性のリスクがある。
多重共線性があるとなぜ問題なのか?
多重共線性があるとなぜ問題なのか?問題であることがわからなければ対処が必要に思えない。
多重共線性がある変数同士を一緒に多変量モデルに入れると、どちらか一方が逆の回帰係数になってしまう。現実とは逆になってしまうのだ。
先ほどの例で、体重と運動量が相関していて、運動量が多いと体重が少ない関係があるとする。また体重と筋肉量が相関していて、筋肉量が多いと体重が多いとする。そして、運動量に比例して筋肉量が多く、その関係が強いとする。
体重を運動量と筋肉量を含んだ多変量モデルで予測する式を作ると、運動量と体重、もしくは筋肉量と体重の関係が、元の関係性とは逆になってしまう。
体重を運動量と筋肉量を含んだ多変量モデルで予測すると、運動量も筋肉量も多いと体重が多いという結果になってしまったりする。または、どちらも少ないと体重が多いという結果になってしまったりする。
これはなぜかと言うと、体重と関係がある運動量と筋肉量がどちらかが相手を譲り合うからなのである。運動量との関係性を重視して、筋肉量との関係はバランスを取るくらいにしか使われない。もしくは筋肉量との関係性を重視して、運動量との関係性は重要視されない。計算上こういうことが起きる。バランスを取るために、回帰係数がゼロに近くなったり、符号が逆になったりする。
体重の変化をとてもよく説明する運動量があった場合、筋肉量の出番がなくなる。逆に体重を筋肉量がとてもよく説明してしまったら、運動量の入るスキがなくなってしまう。
運動量も筋肉量も体重と関係しているのに、それらが反映されない結果は望んでいない結果だ。これは運動量と筋肉量との間にも強い関係があるからなのだ。これが多重共線性の問題点だ。
多重共線性を回避するには?
多重共線性は、VIF Variance Inflation Factor というものを計算して確認できる。10を超える場合、対処が必要になる。VIFの詳細はこちらの記事を参照。

VIFが10を超える変数があった場合どうすればいいか?二つ考えられる。
- その変数をモデルに投入するのをあきらめる
- 主成分回帰 Principal Component Regression を行う
一つずつ見てみよう。
1. その変数をモデルに投入するのをあきらめる
体重を予測するために、運動量と筋肉量のどちらも考慮したい気持ちはわかるが、多重共線性を起こすほど強い相関関係があることが判明した場合は、涙を呑んでどちらかをあきらめて外す。
なぜならば、とても強い相関関係があるのならば、どちらか一方で、もう一方をほとんど表現できているので、どちらかは必要ないからだ。
どうしても予測式に組み込みたい変数のほうを残して、もう一方を割愛する方法がもっとも単純でわかりやすい対処法だ。
2. 主成分回帰 Principal Component Regression PCR を行う
結果はわかりにくくなっても、どうしても多重共線性のある変数を扱った多変量モデルが構築したいということであれば、主成分回帰 Principal Component Regression (PCR) がおすすめだ。
主成分回帰は、まず多数の説明変数に対して、主成分分析を実施して、主成分と呼ばれる合成変数を使った「得点」を計算する。
主成分は、それぞれが独立で、主成分得点同士は多重共線性の心配は無用だ。多重共線性が懸念される変数同士が含まれていても、主成分得点に変換してしまえば、その心配は完全になくなってしまう。
この主成分得点を使って目的変数を予測する回帰式を作る回帰分析を行うのが主成分回帰だ。
主成分得点が、元の変数一つ一つとは直接的につながらない数値になるので、直感的にはわかりにくい結果になるが、多重共線性の懸念がある変数も組み入れたモデルであることは間違いない。希望に応じてこちらの選択肢もあるわけだ。
主成分分析の計算例はこちらを参照。
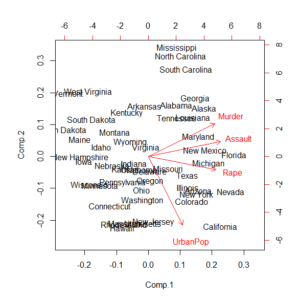
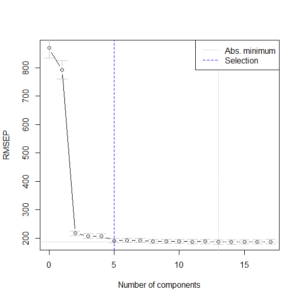
主成分回帰の計算例はこちらを参照のこと。
まとめ
重回帰分析で、多重共線性がある場合に、回避する方法について書いてきた。
改めて、多重共線性とは何かについて書き、なぜ多重共線性が問題なのかに触れ、そして多重共線性問題に対処する方法を二つ挙げた。
多重共線性のある変数の投入をあきらめるのが一番わかりやすく早いのだが、そう簡単にあきらめられない場合は、主成分回帰を使うのがよいと思う。




コメント