R で skewness や kurtosis を計算する方法

R で skewness や kurtosis を計算する方法。

平均と標準偏差

統計ソフトRで、平均値は、mean()で算出する。

標準偏差は、sd()で計算する。

sdはstandard deviationの略。

平均値と標準偏差の値の関係で、データの分布を大まかに推測できる。

平均値が標準偏差の3倍あれば、だいだい正規分布している。

正規分布をしていれば、平均値に±標準偏差の2倍の範囲に、データの約95％が収まる。

> mean(chickwts$weight)
[1] 261.3099
> sd(chickwts$weight)
[1] 78.0737

平均を標準偏差で割ってみると約3倍。

だいたい正規分布していると想像する。

> 261.3099/78.0787
[1] 3.34675

ヒストグラムを見てみる。

だいたい正規分布と言ってよい。

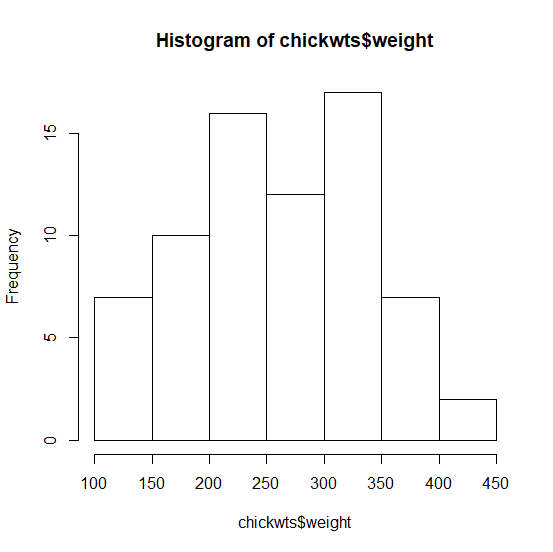
中央値（メディアン）

正規分布していないデータの場合、代表値としてはこちらのほうが望ましい。

chickwtsデータフレーム内のweightの中央値は、平均値とほぼ同じで、ほぼ正規分布なので、平均値と中央値がほぼ同じになる。

> median(chickwts$weight)
[1] 258
> mean(chickwts$weight)
[1] 261.3099

歪度（わいど）Skewness

分布が正規分布から外れてゆがんでいる度合いが歪度だ。

非対称性を表す指標。e1071パッケージに含まれている。

最初一回だけ、e1071パッケージのインストールが必要だ。

install.packages("e1071")

一回のセッションで使い始めの時に一回だけlibrary()で呼び出す。

library(e1071)

歪度を計算する関数はskewness()

例としてx1というデータがあるとする。

x1 <- c(6.0,10.0,7.6,3.5,1.4,2.5,5.6,3.0,2.2,5.0, 3.3,7.6,5.8,6.7,2.8,4.8,6.3,5.3,5.4,3.3, 3.4,3.8,3.3,5.7,6.3,8.4,4.6,2.8,7.9,8.9)

ヒストグラムを見てみると、左右対称ではなくゆがんでいる。

hist(x1)

このとき歪度を計算すると、0.361

> skewness(x1)
[1] 0.3614441

ちなみに、先ほど見たほぼ正規分布している chickwts$weightのskewnessも計算してみると、ほぼゼロ。

分布がゆがんでいると数値の絶対値が大きくなる。

> skewness(chickwts$weight)
[1] -0.01136593

skewnessは3種類ある。

SASやSPSSではType=2だ。

Type=2を使うのが無難だろう。

> skewness(x1, type=2)
[1] 0.4006154

尖度（せんど）Kurtosis

尖度は正規分布と比べて、鋭いピークか鈍いピークかを表す。

> kurtosis(x1)
[1] -0.8275311
> kurtosis(chickwts$weight)
[1] -0.9651994

尖度はx1とchickwts$weightでは、それほど異ならない。

尖度も3種類ありこれもType=2が無難だ。

正規分布であった場合、偏らないのがType=2だけだ。

> kurtosis(x1, type=2)
[1] -0.5726655
> kurtosis(chickwts$weight, type=2)
[1] -0.8843778

ランダム変数で試してみる

ここで、正規分布しているランダム変数を作って、試してみよう。

100個と1000個で比べてみる。

x100は100個のランダム変数。

x1000は1000個のランダム変数。

set.seed(20180504)
x100 <- rnorm(100)
hist(x100)

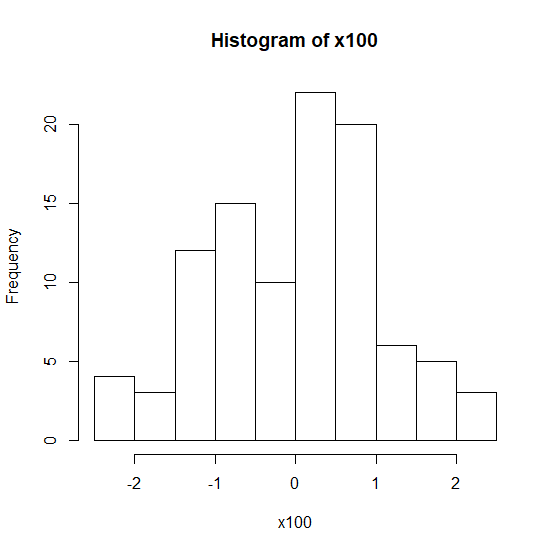
x1000 <- rnorm(1000)
hist(x1000)

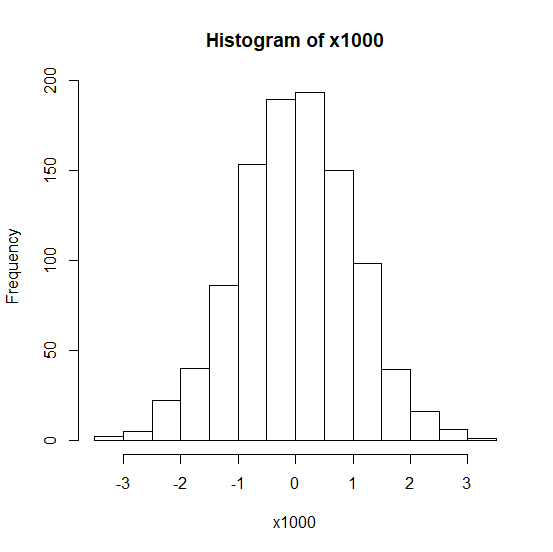
> kurtosis(x100, type=2)
[1] -0.2333893
> kurtosis(x1000, type=2)
[1] -0.002990156

ヒストグラムを見ると、100個より1000個のほうがより正規分布らしい。

尖度は100よりも1000のほうがゼロに近い。

尖度はとがり方がより正規分布に近いかどうかを表す指標だ。

まとめ

通常はデータを眺めてみるときは、平均値と標準偏差でよい。

グラフも大事で、ヒストグラムで分布も見たほうが良い。

ヒストグラムが左右対称の釣り鐘型の分布ではなさそうなら、中央値も確認するとよい。

歪度や尖度は必要に応じて算出する。

参考文献

Package ‘e1071’