主成分分析は、たくさんの変数を、合成変数に集約する分析。
主役級の主成分から第一主成分、第二主成分、・・・と呼ばれる。
たくさんの変数を、いくつかの主成分でまとめると、情報がまとまって考えやすくなる。
Rで主成分分析を行う方法
princomp()を使う。
cor=Tを指定して使う。
cor=Tは相関係数行列を使う指示。
Rで主成分分析 例題1:米国の州をプロファイリング
USArrestsデータという米国の州ごとの犯罪数データを使って、主成分にまとめてみる。
犯罪データは3種類(Murder, Assault, Rape)。
都市人口データを合わせて4つの変数。
主成分分析の本体を実施して、主成分の重要度を確認、主成分負荷量を確認、主成分得点を確認、第一主成分と第二主成分のプロットを描かせるという順番で進めていく。
(pc.cr <- princomp(USArrests, cor = T))
summary(pc.cr)
loadings(pc.cr)
pc.cr$score
biplot(pc.cr)
変数が4つなので、合成変数はComp.1~4の4つが作成される。
> (pc.cr <- princomp(USArrests, cor = T))
Call:
princomp(x = USArrests, cor = T)
Standard deviations:
Comp.1 Comp.2 Comp.3 Comp.4
1.5748783 0.9948694 0.5971291 0.4164494
4 variables and 50 observations.
4つの合成変数の重要性は、合成変数のばらつき(Standard deviation)で評価される。
ばらつきがデータの情報を含んでいる指標になる。
ばらつきが大きいほうがより多くの情報を含んでいる。
> summary(pc.cr)
Importance of components:
Comp.1 Comp.2 Comp.3 Comp.4
Standard deviation 1.5748783 0.9948694 0.5971291 0.41644938
Proportion of Variance 0.6200604 0.2474413 0.0891408 0.04335752
Cumulative Proportion 0.6200604 0.8675017 0.9566425 1.00000000
負荷量の大きさや符号から合成変数を解釈する。
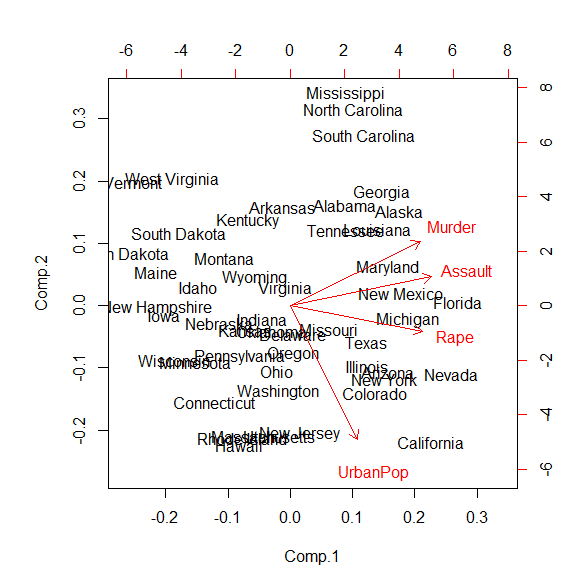
第一主成分Comp.1はMurder、Assault、Rapeの負荷量が大きく、UrbanPopは小さめだ。
第一主成分はMurder, Assault, Rapeが多いか少ないかの合成変数と解釈する。
Comp.2はUrbanPopが負の値で大きい。
Murderもそこそこ負荷量が大きいがこちらは割愛して、第二主成分は都市部の人口の多い少ないを表していると解釈する。
> loadings(pc.cr)
Loadings:
Comp.1 Comp.2 Comp.3 Comp.4
Murder 0.536 0.418 0.341 0.649
Assault 0.583 0.188 0.268 -0.743
UrbanPop 0.278 -0.873 0.378 0.134
Rape 0.543 -0.167 -0.818
Comp.1 Comp.2 Comp.3 Comp.4
SS loadings 1.00 1.00 1.00 1.00
Proportion Var 0.25 0.25 0.25 0.25
Cumulative Var 0.25 0.50 0.75 1.00
合成変数(得点、スコア、Score)を表示してみる。
それぞれの州の犯罪、人口データに、各変数の負荷量をかけて足し合わせると、州ごとの合成変数=主成分得点が計算される。
> pc.cr$score
Comp.1 Comp.2 Comp.3 Comp.4
Alabama 0.98556588 1.13339238 0.44426879 0.156267145
Alaska 1.95013775 1.07321326 -2.04000333 -0.438583440
Arizona 1.76316354 -0.74595678 -0.05478082 -0.834652924
Arkansas -0.14142029 1.11979678 -0.11457369 -0.182810896
California 2.52398013 -1.54293399 -0.59855680 -0.341996478
Colorado 1.51456286 -0.98755509 -1.09500699 0.001464887
Connecticut -1.35864746 -1.08892789 0.64325757 -0.118469414
Delaware 0.04770931 -0.32535892 0.71863294 -0.881977637
Florida 3.01304227 0.03922851 0.57682949 -0.096284752
Georgia 1.63928304 1.27894240 0.34246008 1.076796812
Hawaii -0.91265715 -1.57046001 -0.05078189 0.902806864
Idaho -1.63979985 0.21097292 -0.25980134 -0.499104101
Illinois 1.37891072 -0.68184119 0.67749564 -0.122021292
Indiana -0.50546136 -0.15156254 -0.22805484 0.424665700
Iowa -2.25364607 -0.10405407 -0.16456432 0.017555916
Kansas -0.79688112 -0.27016470 -0.02555331 0.206496428
Kentucky -0.75085907 0.95844029 0.02836942 0.670556671
Louisiana 1.56481798 0.87105466 0.78348036 0.454728038
Maine -2.39682949 0.37639158 0.06568239 -0.330459817
Maryland 1.76336939 0.42765519 0.15725013 -0.559069521
Massachusetts -0.48616629 -1.47449650 0.60949748 -0.179598963
Michigan 2.10844115 -0.15539682 -0.38486858 0.102372019
Minnesota -1.69268181 -0.63226125 -0.15307043 0.067316885
Mississippi 0.99649446 2.39379599 0.74080840 0.215508013
Missouri 0.69678733 -0.26335479 -0.37744383 0.225824461
Montana -1.18545191 0.53687437 -0.24688932 0.123742227
Nebraska -1.26563654 -0.19395373 -0.17557391 0.015892888
Nevada 2.87439454 -0.77560020 -1.16338049 0.314515476
New Hampshire -2.38391541 -0.01808229 -0.03685539 -0.033137338
New Jersey 0.18156611 -1.44950571 0.76445355 0.243382700
New Mexico 1.98002375 0.14284878 -0.18369218 -0.339533597
New York 1.68257738 -0.82318414 0.64307509 -0.013484369
North Carolina 1.12337861 2.22800338 0.86357179 -0.954381667
North Dakota -2.99222562 0.59911882 -0.30127728 -0.253987327
Ohio -0.22596542 -0.74223824 0.03113912 0.473915911
Oklahoma -0.31178286 -0.28785421 0.01530979 0.010332321
Oregon 0.05912208 -0.54141145 -0.93983298 -0.237780688
Pennsylvania -0.88841582 -0.57110035 0.40062871 0.359061124
Rhode Island -0.86377206 -1.49197842 1.36994570 -0.613569430
South Carolina 1.32072380 1.93340466 0.30053779 -0.131466685
South Dakota -1.98777484 0.82334324 -0.38929333 -0.109571764
Tennessee 0.99974168 0.86025130 -0.18808295 0.652864291
Texas 1.35513821 -0.41248082 0.49206886 0.643195491
Utah -0.55056526 -1.47150461 -0.29372804 -0.082314047
Vermont -2.80141174 1.40228806 -0.84126309 -0.144889914
Virginia -0.09633491 0.19973529 -0.01171254 0.211370813
Washington -0.21690338 -0.97012418 -0.62487094 -0.220847793
West Virginia -2.10858541 1.42484670 -0.10477467 0.131908831
Wisconsin -2.07971417 -0.61126862 0.13886500 0.184103743
Wyoming -0.62942666 0.32101297 0.24065923 -0.166651801
第一主成分と第二主成分をX軸とY軸にとり、州をプロットしてみると、下記のように描ける。
犯罪が多い少ないと都市部人口が多い少ないで、州をプロファイリングできる。
4つのデータから二軸にプロファイリングできた。
情報が集約できたと言える。
Rで主成分分析 例題2:米国上位裁判所の州判事を弁護士が評価した!
USJudgeRatingsデータは、米国の上位裁判所の州判事43人を弁護士が12の観点で評価したデータ。
主成分分析本体、Standard deviationのチェック、負荷量のチェック、第一主成分と第二主成分のプロットの順番に進める。
princomp(USJudgeRatings, cor=T)
summary(princomp(USJudgeRatings, cor=T))
loadings(princomp(USJudgeRatings, cor=T))
biplot(princomp(USJudgeRatings, cor=T))
第一主成分と第二主成分のStandard deviationが1を超えているのがわかる。
変数が12個あるので、合成変数も12個作られる。
> princomp(USJudgeRatings, cor=T)
Call:
princomp(x = USJudgeRatings, cor = T)
Standard deviations:
Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6 Comp.7
3.18331647 1.05078398 0.57697626 0.50383231 0.29060762 0.19309598 0.14029545
Comp.8 Comp.9 Comp.10 Comp.11 Comp.12
0.12415832 0.08850690 0.07491146 0.05708042 0.04539134
12 variables and 43 observations.
第一主成分と第二主成分で94%を説明していると解釈できる。
> summary(princomp(USJudgeRatings, cor=T))
Importance of components:
Comp.1 Comp.2 Comp.3 Comp.4 Comp.5
Standard deviation 3.1833165 1.05078398 0.5769763 0.50383231 0.290607615
Proportion of Variance 0.8444586 0.09201225 0.0277418 0.02115392 0.007037732
Cumulative Proportion 0.8444586 0.93647089 0.9642127 0.98536661 0.992404341
Comp.6 Comp.7 Comp.8 Comp.9 Comp.10
Standard deviation 0.193095982 0.140295449 0.124158319 0.0885069038 0.0749114592
Proportion of Variance 0.003107172 0.001640234 0.001284607 0.0006527893 0.0004676439
Cumulative Proportion 0.995511513 0.997151747 0.998436354 0.9990891437 0.9995567876
Comp.11 Comp.12
Standard deviation 0.0570804224 0.0453913429
Proportion of Variance 0.0002715146 0.0001716978
Cumulative Proportion 0.9998283022 1.0000000000
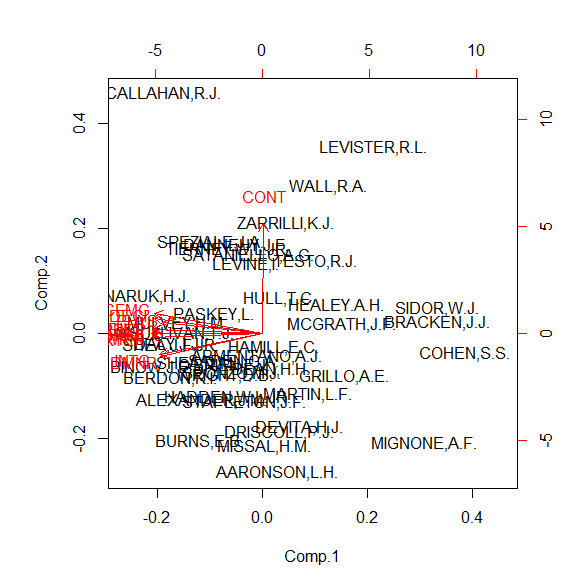
第一主成分はCONT以外はすべて負で絶対値が0.3くらいでそろっている。
第二主成分はCONTだけが突出している。
CONTは、弁護士が判事とどのくらいコンタクトしているか。
ほかの変数は判事としての能力や素質の評価だ。
コンタクトが多い少ないはほかの変数とは性質が異なるので、第一主成分の合成変数の一員として入りにくかったと想像できる。
> loadings(princomp(USJudgeRatings, cor=T))
Loadings:
Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6 Comp.7 Comp.8 Comp.9 Comp.10 Comp.11 Comp.12
CONT 0.933 0.335
INTG -0.289 -0.182 0.549 0.174 -0.370 -0.450 -0.334 0.275 -0.109 -0.113
DMNR -0.287 -0.198 0.556 -0.124 -0.229 0.395 0.467 0.247 0.199 0.134
DILG -0.304 -0.164 0.321 -0.302 -0.599 0.210 0.355 0.383
CFMG -0.303 0.168 -0.207 -0.448 0.247 -0.714 -0.143 0.166
DECI -0.302 0.128 -0.298 -0.424 0.393 -0.536 0.302 0.258 -0.128
PREP -0.309 -0.152 0.214 0.203 0.335 0.154 0.109 -0.680 -0.319 0.273
FAMI -0.307 -0.195 0.201 0.507 0.102 0.223 0.573 -0.422
ORAL -0.313 0.246 0.150 -0.300 0.256 -0.639 -0.494
WRIT -0.311 0.137 0.306 0.238 -0.126 0.475 0.696
PHYS -0.281 -0.154 -0.841 0.118 -0.299 0.266
RTEN -0.310 0.173 -0.184 -0.256 0.221 -0.756 -0.250 0.286
Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6 Comp.7 Comp.8 Comp.9 Comp.10 Comp.11
SS loadings 1.000 1.000 1.000 1.000 1.000 1.000 1.000 1.000 1.000 1.000 1.000
Proportion Var 0.083 0.083 0.083 0.083 0.083 0.083 0.083 0.083 0.083 0.083 0.083
Cumulative Var 0.083 0.167 0.250 0.333 0.417 0.500 0.583 0.667 0.750 0.833 0.917
Comp.12
SS loadings 1.000
Proportion Var 0.083
Cumulative Var 1.000
第一主成分と第二主成分のプロットはコンタクトが多いか少ないかと素質・能力が評価できるかどうかの二軸。
どんな判事か想像がつけば、プロファイリングとして面白いはず。
まとめ
主成分分析は、たくさんの変数を、集約して、いくつかの合成変数で表現しなおす、情報集約のための分析方法。
第一主成分と第二主成分にまとまると、平面で図示できるため理解しやすい。
Rでは、princomp()関数を、cor=Tと指定して分析する。
biplot()で第一主成分と第二主成分のプロットを行うと、想像が膨らみ、主成分とデータの解釈がしやすくなる。








コメント
コメント一覧 (1件)
[…] R で主成分分析を行う方法 主成分分析は、たくさんの変数を、合成変数に集約する分析。 […]