R で ROC 曲線を書く方法

ROC 曲線を R で書く方法をわかりやすく解説

ROC 曲線とは？

ROC曲線は、病気の診断のための検査を分析するために使われる。

真実の分類と、真実の分類を見分ける検査結果を使って、どのレベルより上だと病気とするか？を決める分析ツール。

胃がんや大腸がんを見つけるには、内視鏡をしないと見つけられないが、簡単な血液検査で見つけたいとする。

血液検査の値がいくつのときに、がんとがんではないかを一番クリアに分けることができるか？

こういう問題に答えられる。

ROC 曲線を R で書いてみるためのサンプルデータ

データは、KTSND という検査の点数（連続データとして扱う）と、SMK が正解の分類（二値のカテゴリカルデータ）。

KTSND のカットオフ値としていくつがもっとも SMK を予測するかという分析になる。

> str(dat)
'data.frame':   484 obs. of  2 variables:
$ KTSND: int  15 13 16 4 18 29 15 15 11 6 ...
$ SMK  : int  1 1 1 1 1 1 1 1 1 0 ...

ROC 曲線を R で書くためのパッケージのインストール

Epi というパッケージをインストールする。

install.packages("Epi")

そのあと呼び出して使えるようにする。

library(Epi)

ROC 曲線を R で書いてみる

データをdatという名前で読み込む。

dat <- read.table("ROC-curve-sample-data.txt")

plot=”ROC”でROC曲線分析を指定。

ROC(test=dat$KTSND, stat=dat$SMK, plot="ROC")

test= で検査値、stat= で正解の分類を指定する。

そうすると、以下のグラフ（黒い太めの実線）が描ける。

ガタガタしていてあまりなめらかでないが、一応曲線に見えなくもない。

これが ROC 曲線である。

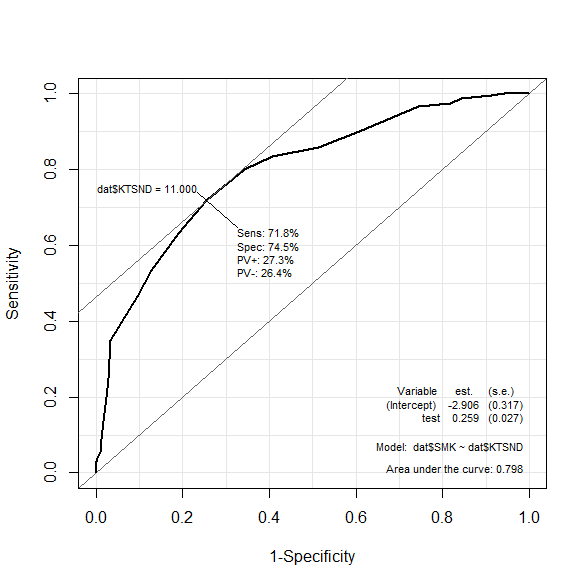
KTSNDが11点のときが、一番うまくわけている分岐点であると、示している。

このカットオフ値としたときの以下の 4 つの指標が表示されている。

• Sens （感度）71.8%
• Spec（特異度）74.5%
• PV+（陽性反応的中率）27.3%
• PV-（陰性反応的中率）26.4%

AUCは0.798で、この検査自体性能がいい証拠だ。

AUCがなるべく1に近いほうがいい。

正方形の面積が1だ。

右下をかなめとみて、扇形がAUCで今回は約0.8だ。

ROC 曲線以外にも感度・特異度・的中率のグラフも書ける

先ほど plot=”ROC” と指定したところを plot=”sp” とする。

plot=”sp”は感度、特異度、的中率を表示する指定。

ROC(test=dat$KTSND, stat=dat$SMK, plot="sp")

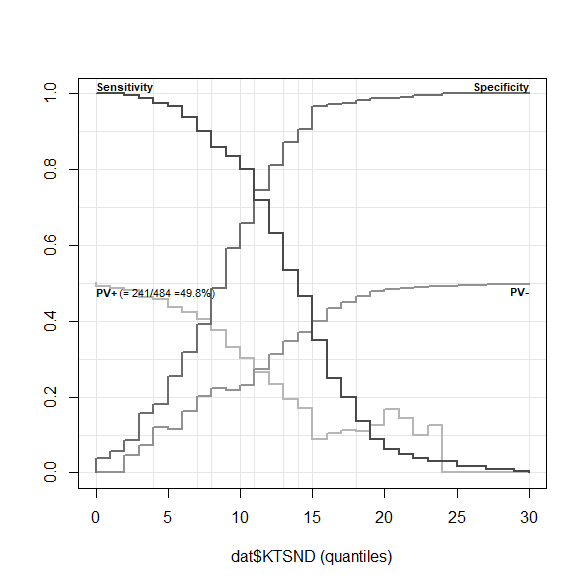
Sensitivity（感度）とSpecificity（特異度）が交わるところが11点だ。

陽性反応的中率は最大でも49.8%までしか到達しないことがわかる。

まとめ

Rで、ROC曲線を書くには、Epi パッケージの ROC() 関数を使うのが便利だ。

とてもきれいな図が簡単に描ける。

参考リンク

Epi: A package for statistical analysis in epidemiology

参考書籍