級内相関係数 ICC Case2 の計算とサンプルサイズ計算を R でやってみた
級内相関係数 ICC(2,1) の計算例
級内相関係数 Intra-class Correlation Coefficient Case2 ICC Case2 は検者間信頼性の指標。
患者さんを数名の検査者（または評価者）で検査（または評価）して、その測定値の一致性を見るのが主目的。
複数の検査者が各患者さん 1 回ずつ検査・評価した場合の ICC(2,1) が良く用いられる。
9人の患者さんをA～Eの5人の検査者で1回ずつ検査した時
irrパッケージのicc()を使う。
最初一回だけインストールする。
install.packages("irr")
データ拝借元：級内相関係数｜統計解析ソフト エクセル統計
A <- c(0,2,2,1,3,0,4,4,6)
B <- c(0,4,1,2,3,1,5,4,6)
C <- c(0,2,0,0,3,0,4,4,6)
D <- c(0,2,2,1,3,0,4,5,4)
E <- c(0,3,2,1,3,0,4,4,6)
dat.twoway <- cbind(A,B,C,D,E)
rownames(dat.twoway) <- c(1:9)
dat.twoway
library(irr)
icc(dat.twoway, model="twoway", type="agreement")
ICC(2,1) の計算結果は以下の通り。
> library(irr)
> icc(dat.twoway, model="twoway", type="agreement")
Single Score Intraclass Correlation
Model: twoway
Type : agreement
Subjects = 9
Raters = 5
ICC(A,1) = 0.906
F-Test, H0: r0 = 0 ; H1: r0 > 0
F(8,32.8) = 55.6 , p = 6.98e-17
95%-Confidence Interval for ICC Population Values:
0.783 < ICC < 0.974
ICC(2,1)は、0.906と計算された。
高い一致度だ。
患者さん10人をA～Dの4人の検査者で膝関節屈曲可動域を検査した時
別のデータでICC(2,1)を計算してみる。
患者さん10人、A～Dの4人の検査者で、膝関節屈曲可動域を検査したデータだ。
データ拝借元：信頼性指標としての級内相関係数
A <- c(126,137,113,153,146,161,110,145,126,114)
B <- c(122,143,119,143,157,157,109,151,141,126)
C <- c(131,141,115,135,150,160,105,152,132,130)
D <- c(125,141,105,144,149,160,113,156,122,125)
dat.twoway <- cbind(A,B,C,D)
rownames(dat.twoway) <- c(1:10)
dat.twoway
icc(dat.twoway, model="twoway", type="agreement")
計算結果は以下の通り。
> icc(dat.twoway, model="twoway", type="agreement")
Single Score Intraclass Correlation
Model: twoway
Type : agreement
Subjects = 10
Raters = 4
ICC(A,1) = 0.909
F-Test, H0: r0 = 0 ; H1: r0 > 0
F(9,30) = 40.4 , p = 2.46e-14
95%-Confidence Interval for ICC Population Values:
0.788 < ICC < 0.973
ICC(2,1)は0.909と計算された。
こちらも一致度が高い。
irrパッケージのanxietyデータを使った例
20人の患者さんを3人の評価者が評価した結果のICC。
data(anxiety)
icc(anxiety, model="twoway", type="agreement")
ICC(2,1)は0.198とかなり低い一致度。
> icc(anxiety, model = "twoway", type = "agreement")
Single Score Intraclass Correlation
Model: twoway
Type : agreement
Subjects = 20
Raters = 3
ICC(A,1) = 0.198
F-Test, H0: r0 = 0 ; H1: r0 > 0
F(19,39.7) = 1.83 , p = 0.0543
95%-Confidence Interval for ICC Population Values:
-0.039 < ICC < 0.494
irrパッケージのDiagnosesデータを使った場合
精神科領域の疾患の診断が評価者によってどれだけ一致するかというデータ。
患者さん30人、評価者6人のデータ。
diagnoses.rev <- matrix(c(diagnoses[,1],diagnoses[,2],diagnoses[,3],diagnoses[,4],diagnoses[,5],diagnoses[,6]),nr=30)
icc(diagnoses.rev, model = "twoway", type = "agreement")
ICC(2,1)はあまり高くなく0.373にとどまった。
> icc(diagnoses.rev, model = "twoway", type = "agreement")
Single Score Intraclass Correlation
Model: twoway
Type : agreement
Subjects = 30
Raters = 6
ICC(A,1) = 0.373
F-Test, H0: r0 = 0 ; H1: r0 > 0
F(29,33.7) = 7.03 , p = 1.21e-07
95%-Confidence Interval for ICC Population Values:
0.196 < ICC < 0.572
級内相関係数 ICC(2,1) のサンプルサイズ計算
級内相関係数 ICC(2,1) のサンプルサイズ計算はどうやるのだろうか？
参考文献 Doros G. and Lew R. Design Based on Intra-Class Correlation Coefficients. Am J Biostatistics 2010: 1 (1); 1-8.に計算結果が掲載されている。
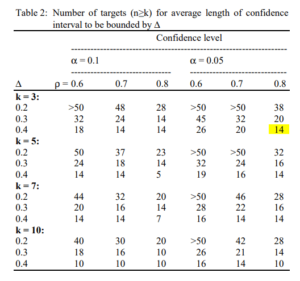
検査者が3人、5人、7人、10人のとき、信頼区間全体の平均幅 $ \Delta $ が0.2、0.3、0.4のときのサンプルサイズが計算されている。
信頼区間の有意水準が10%（$ \alpha $ = 0.1）のときと5%（$ \alpha $ = 0.05）の時が計算されている。
ICC(2,1)の推定値 $ \rho $ が0.6、0.7、0.8のときがそれぞれ計算されている。
例えば、検査者が3人(k=3)で、信頼区間幅が0.4で推定したいとする。
有意水準5%つまり95%信頼区間で推定するとして、$ \rho $ が 0.8 と推定されるとすると、必要なサンプルサイズ（患者さんの人数）は14人である。
参考文献にはスクリプトの請求が可能と書いてあった。
論文に掲載されていない数値に関しては、各自スクリプトを取り寄せて、スクリプトを確認の上、計算してもらいたい。
計算における注意点
実際の計算には、variance ratio $ \sigma_T^2 / \sigma_E^2 $ 、想定する ICC(2,1) の値 $ \rho $ が必要になる。
$ \rho $ と variance ratio には、以下の関係がある。
$$ \rho = \frac{\sigma_T^2 / \sigma_E^2} {\sigma_T^2 / \sigma_E^2 + \sigma_J^2 / \sigma_E^2 + 1} $$
ここで、
- $ \sigma_T^2 $: variance of normally distributed random target effects（目標とする効果の分散）
- $ \sigma_J^2 $: variance of normally distributed random rater effects（評価者効果の分散）
- $ \sigma_E^2 $: variance of normally distributed measurement errors（誤差の分散）
である。
論文中では、variance ratio を pilot study から持ってきている。
Pilot study がない場合、この variance ratio を見極めるのが難しそうだ。
まとめ
級内相関係数 ICC(2,1) の計算例とサンプルサイズ計算の方法を解説した。
参考になれば。
参考文献
参考サイト・PDF
Sample Size Determination for ICC(2,1)
How should we calculate sample size for ICC(2,1) analysis?
A part of sample size calculation for ICC(2,1) with certain conditions were published in the following scientific article:
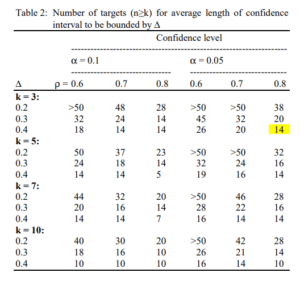
The article showed results of sample size calculation under the condition estimating the confidence intervals of 0.2, 0.3, or 0.4 with two, three, or four raters.
Results with 10% and 5% of alpha levels were exhibited in Table 2 of the article.
Estimates $ \rho $ of 0.6, 0.7, or 0.8 were demonstrated.
For example, if you would estimate $ \rho $ = 0.8 with 0.4 of 95% confidence interval rated by four examiners, 14 patients would be needed as we can see a highlighted number in the following.
The reference said anyone can request R scripts for the calculation.
Please obtain and confirm the scripts, and perform calculation individually for any settings not included in the paper.
コメント