MMRMは、Mixed Model with Repeated Measuresの略である。
反復測定の連続データを線形混合モデルで解析することを意味している。
この試験・研究デザインのとき、サンプルサイズ計算はどのようにしたらよいか?
MMRMのサンプルサイズ計算サイト
以下のサイトのプログラムを用いると計算できる。
MMRMに対するサンプルサイズ設計 | Kengo Nagashima – Keio University
理論はさておき、使い方に特化して、紹介してみたいと思う。
MMRM のサンプルサイズ計算のため サンプルデータはEZR公式マニュアルから
サンプルデータは、EZR公式マニュアルのデータの一部を抜粋して使用する。
EZR公式マニュアル
計算プログラムのサイトと同じくちょうど4回の反復測定であるので、デフォルト設定がそのまま使える。
MMRM のサンプルサイズ計算の前提 1:反復測定目的変数の相関行列
一番最初に群別の相関行列というのが目に入る。

これは、反復測定している目的変数同士の相関行列を示している。
対角線上は同じ時点の測定値同士なので相関係数は1である。
それ以外は、異なる時点同士の測定値同士の相関係数である。
実際は、以下のように時点ごとの相関はばらばらである。


であるが、計算プログラムのサイトの例のように、時点同士の相関は同じとみなして進めることがある。
この形を compound symmetry (SPSSでは複合シンメトリ)と呼ぶ。

実際の値は上記のようにバラバラなので、それがわかる場合は、そのバラバラを使うこともある。
バラバラの相関係数行列の場合は、無構造 (unstructured) と呼ばれる。
今回は、デフォルトの compound symmetry のままで進める。
MMRM のサンプルサイズ計算の前提 2:欠測の発生割合
次に決めないといけないのは、欠測の値が発生する割合。
非欠測の割合とあって、どのくらいの割合がきちんと観測されるかという数値を入れる。
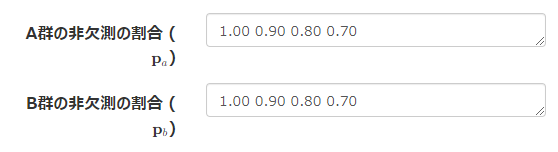
デフォルトでは、100%, 90%, 80%, 70%とだんだんに脱落していくことを想定をしている。
脱落はほぼないことが予想されるなら、全部100% とか、下がっても90%とかするとよいと思う。
こちらもデフォルトのままでいく。
MMRM のサンプルサイズ計算の前提 3:群別の標準偏差
次に必要な情報は、標準偏差である。
群別の標準偏差である。
どの測定時点ということでもなく、どの測定時点も同じ標準偏差(分散)が前提となる。
サンプルデータの群別・時点別目的変数の標準偏差を計算すると以下のようになる。
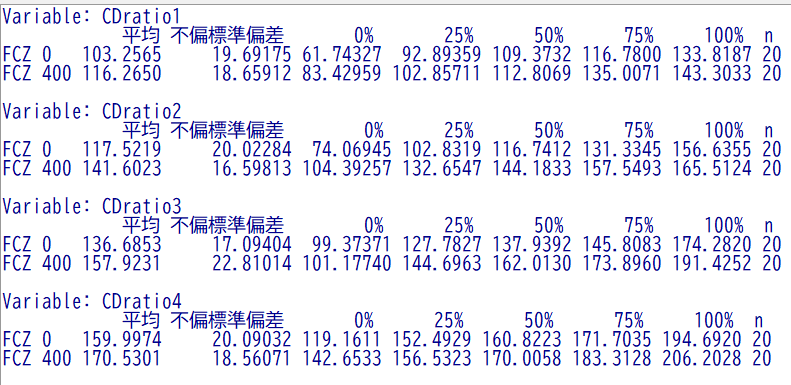
FCZ0群は、19.7, 20.0, 17.1, 20.1ということなので、大体19くらいとする。
FCZ400群は、18.7, 16.6, 22.8, 18.6であるので、こちらも大体19と考えることができる。

なので、両方に19と入れる。
割付比は1にしておく。
特別な理由がない限り、割付比は1:1がもっとも検出力が高く望ましいためである。
MMRM のサンプルサイズ計算の前提4:群間差(標準偏差を1とすれば効果量)
最後群間差である。
上記の連続変数の要約値の出力から手計算で、大体17くらいと推定できる。
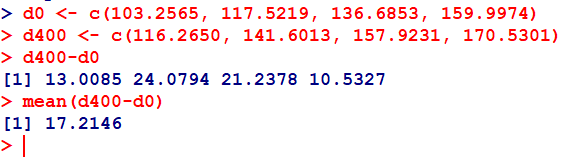
なので、群間差は17とする。
あとは、両側検定、t検定、α(有意水準)0.05、1-β(検出力)0.8とのデフォルトのまま、Submitをクリックする。
MMRM の必要なサンプルサイズ
右側に計算結果が出力される。
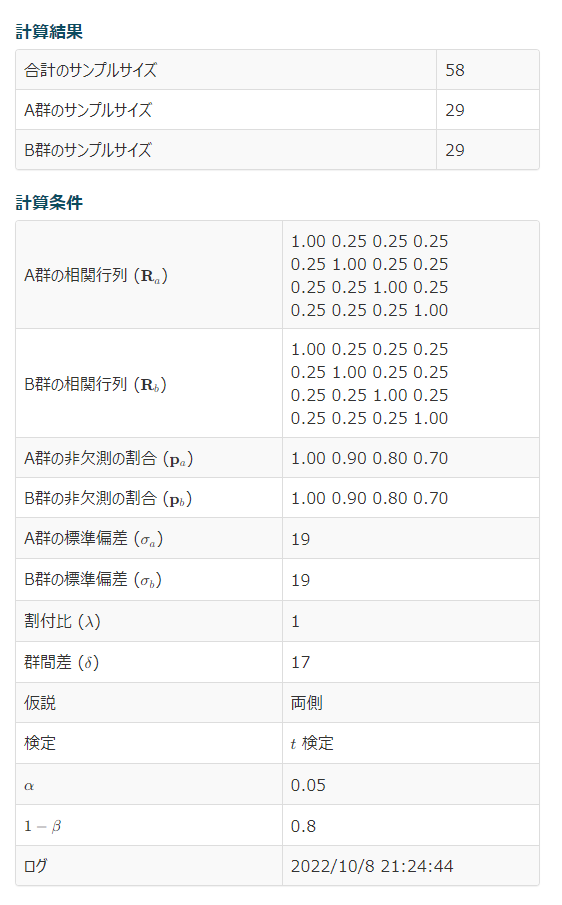
合計のサンプルサイズが58、A・B群ともにサンプルサイズは29、と計算されている。
サンプルデータは40例であるので、サンプルサイズ計算上は1.5倍程度のサンプルサイズが必要とのことである。
非欠測の値を大きく(つまり欠測の割合を小さく)すると、必要なサンプルサイズは小さくなる。
やはり、欠測はなるべく少ないのに越したことはないようである。
MMRM のサンプルサイズ計算のためのサンプルデータの視覚化・解析結果
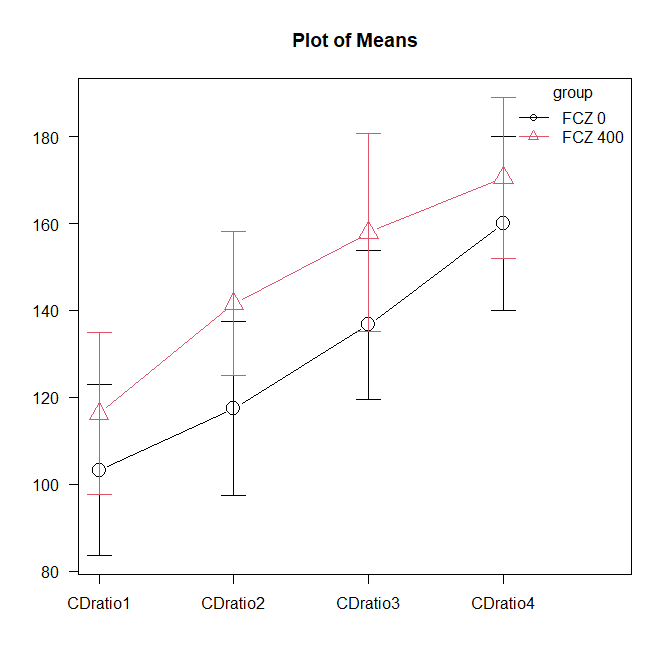
ちなみにサンプルとして使っているデータの平均値グラフは以下のようになる。
2つの群がきっちり離れている。
統計解析結果も、群の効果は統計学的有意である(ハイライト部分)。
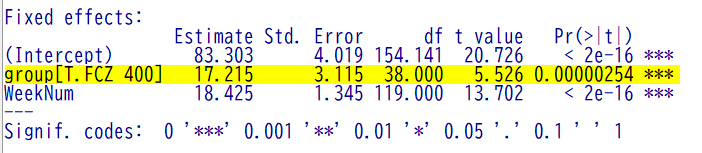
なので、サンプリングしたデータによっては、サンプルサイズが小さくても統計学的有意になりうる。
しかしながら、できれば事前にサンプルサイズを見積もってから試験なり、研究データ収集なりに進んだほうが、あとあと安心できる。
まとめ
MMRMと呼ばれる反復測定の線形混合モデルのサンプルサイズ計算プログラムサイトの使い方を紹介した。
MMRMに対するサンプルサイズ設計 | Kengo Nagashima – Keio University
いろいろと前提条件を入れる必要がある。
先行研究やパイロット研究を参考にしてなるべく確実な前提条件を入れたい。
参考になれば。
計算プログラムサイト
MMRMに対するサンプルサイズ設計 | Kengo Nagashima – Keio University
おすすめ書籍
EZR公式マニュアル









コメント