生存時間解析のサンプルサイズ計算の方法
Cox の比例ハザードモデルを使う前提の計算
生存時間解析のサンプルサイズ計算 その 1
R でスクリプトを書いてみた。
S0がコントロール、S1が治療群、それぞれの生存率。
dが、両群合わせて合計の死亡者数。
sample.size.cox <- function(S1,S0,alternative="two.sided",power=.8,
sig.level=.05){
alternative <- match.arg(alternative)
tside <- switch(alternative, one.sided=1, two.sided=2)
beta <- log(log(S1)/log(S0))
Za <- qnorm(sig.level/tside, lower.tail=FALSE)
Zb <- qnorm(power)
d <- ((Za+Zb)*(1+exp(beta))/(1-exp(beta)))^2
NOTE <- "d is total number of death in *both* of groups"
METHOD <- "Sample Size Calculation of Cox Propotional Hazard Model"
structure(
list("Total number of death" = d,
"Surv. rate of trt. arm" = S1,
"Surv. rate of ctl. arm" = S0,
"Hazard ratio" = exp(beta),
sig.level = sig.level,
power = power,
alternative = alternative,
note = NOTE,
method = METHOD),
class = "power.htest")
}
治療群の生存率が0.6、コントロールの生存率が0.5のとき、両群合わせて死亡者数が343例必要と計算される。
> sample.size.cox(S1=0.6, S0=0.5)
Sample Size Calculation of Cox Propotional Hazard Model
Total number of death = 342.267
Surv. rate of trt. arm = 0.6
Surv. rate of ctl. arm = 0.5
Hazard ratio = 0.7369656
sig.level = 0.05
power = 0.8
alternative = two.sided
NOTE: d is total number of death in *both* of groups最近の抗がん剤は寿命延長が期待できるものも出てきたので、例えば5年でS1=0.8、S0=0.3というように、中央値に届かないアームも存在する。
0.8 vs 0.3となると、死亡症例数は17例で済み、ハザード比は0.19という極めて低い値が想定される。
> sample.size.cox(S1=0.8, S0=0.3)
Sample Size Calculation of Cox Propotional Hazard Model
Total number of death = 16.6165
Surv. rate of trt. arm = 0.8
Surv. rate of ctl. arm = 0.3
Hazard ratio = 0.1853394
sig.level = 0.05
power = 0.8
alternative = two.sided
NOTE: d is total number of death in *both* of groups生存時間解析のサンプルサイズ計算 その 2
R を使って自前でスクリプトに起こした関数を使う方法
Freedmanの方法とSchoenfeldの方法。
こちらは観察期間を設定してハザードを計算してくれるスクリプトだが、ハザード比は観察期間が異なっても同じで、サンプルサイズも同じである。
比例ハザードモデルの「比例」の由来通り、観察期間にかかわらず比例関係が一定で、観察期間が変わっても、必要なサンプルサイズは変わらない。
- t: 観察期間(年)
- S1 と S0: 治療群とコントロール群の生存率
- dF: Freedmanの方法による各群必要な死亡症例数
- dS: Schoenfeldの方法による各群必要な死亡症例数
sample.size.cox <- function(t,S1,S0,alternative="two.sided",power=.8,
sig.level=.05){
alternative <- match.arg(alternative)
tside <- switch(alternative, one.sided=1, two.sided=2)
beta <- log(log(S1)/log(S0))
H1 <- -1*log(S1)/t
H0 <- -1*log(S0)/t
HR <- H1/H0
Za <- qnorm(sig.level/tside, lower.tail=FALSE)
Zb <- qnorm(power)
dF <- (Za+Zb)^2*(HR+1)^2/(2*(HR-1)^2)
nF <- dF/(((1-S1)+(1-S0))/2)
dS <- 2*(Za+Zb)^2/((log(HR))^2)
nS <- dS/(((1-S1)+(1-S0))/2)
NOTE <- "n is number in *each* group"
METHOD <- "Sample Size Calculation of Cox Propotional Hazard Model"
structure(
list(
"Death (Freedman)" = dF,
"Number (Freedman)" = nF,
"Death (Schoenfeld)" = dS,
"Number(Schoenfeld)" = nS,
"Survival trt" = S1,
"Survival ctl" = S0,
"Hazard trt" = H1,
"Hazard ctl" = H0,
"Hazard ratio" = HR,
"Follow up(y)" = t,
sig.level = sig.level,
power = power,
alternative = alternative,
note = NOTE,
method = METHOD),
class = "power.htest")
}
5年の観察期間で、治療群が生存率0.8、コントロール群が生存率0.65と想定すると、必要死亡症例数は、Freedmanの方法で各39例、Schoenfeldの方法で各37例と計算される。
全体の必要症例数はFreedmanで各142例、Schoenfeldで各132例。
> sample.size.cox(t=5, S1=0.8, S0=0.65)
Sample Size Calculation of Cox Propotional Hazard Model
Death (Freedman) = 38.92388
Number (Freedman) = 141.5414
Death (Schoenfeld) = 36.27976
Number(Schoenfeld) = 131.9264
Survival trt = 0.8
Survival ctl = 0.65
Hazard trt = 0.04462871
Hazard ctl = 0.08615658
Hazard ratio = 0.5179954
Follow up(y) = 5
sig.level = 0.05
power = 0.8
alternative = two.sided
NOTE: n is number in *each* group治療群0.6、コントロール群0.5で計算すると、観察期間が1年でも5年でも同様で、
- Freedmanでは死亡症例は各群172例、全体症例は各群381例必要、
- Schoenfeldでは死亡症例は各群169例、全体症例は各群375例必要
と計算される。
> sample.size.cox(t=1, S1=0.6, S0=0.5)
Sample Size Calculation of Cox Propotional Hazard Model
Death (Freedman) = 171.1335
Number (Freedman) = 380.2966
Death (Schoenfeld) = 168.5111
Number(Schoenfeld) = 374.4692
Survival trt = 0.6
Survival ctl = 0.5
Hazard trt = 0.5108256
Hazard ctl = 0.6931472
Hazard ratio = 0.7369656
Follow up(y) = 1
sig.level = 0.05
power = 0.8
alternative = two.sided
NOTE: n is number in *each* group
5年観察で、治療群が0.8、コントロール群が0.3の場合、FreedmanとSchoenfeldの方法で、それぞれ各群死亡症例は9例、6例、全体症例は各群、19例、13例、が必要と計算される。
> sample.size.cox(t=5, S1=0.8, S0=0.3)
Sample Size Calculation of Cox Propotional Hazard Model
Death (Freedman) = 8.308251
Number (Freedman) = 18.46278
Death (Schoenfeld) = 5.525171
Number(Schoenfeld) = 12.27816
Survival trt = 0.8
Survival ctl = 0.3
Hazard trt = 0.04462871
Hazard ctl = 0.2407946
Hazard ratio = 0.1853394
Follow up(y) = 5
sig.level = 0.05
power = 0.8
alternative = two.sided
NOTE: n is number in *each* group
EZR を使った方法
5年の観察期間で、治療群が生存率0.8、コントロール群が生存率0.65の条件で、EZRを使って計算してみると、Freedman式と同じ141例と計算された。
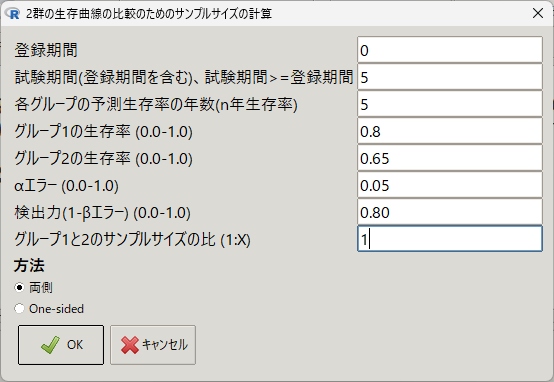
観察研究のイメージで、登録は同時に行われることを想定して、登録期間はゼロとした。
> SampleHazard(0, 5, 5, 0.8, 0.65, 0.05, 0.80, 2, 1)
仮定
P1 0.8
P2 0.65
P1、P2の観察期間 5
登録期間 0
全研究期間 5
αエラー 0.05
両側検定
検出力 0.8
N2とN1のサンプルサイズの比 1
必要サンプルサイズ 計算結果
N1 141
N2 141
治療群0.6、コントロール群0.5、観察期間5年で、EZRで同様に計算してみた。
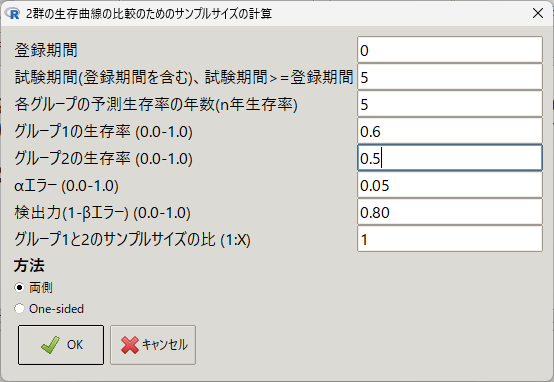
上記のFreedman式の結果と同様に一群380例必要と計算された。
> SampleHazard(0, 5, 5, 0.6, 0.5, 0.05, 0.80, 2, 1)
仮定
P1 0.6
P2 0.5
P1、P2の観察期間 5
登録期間 0
全研究期間 5
αエラー 0.05
両側検定
検出力 0.8
N2とN1のサンプルサイズの比 1
必要サンプルサイズ 計算結果
N1 380
N2 380
1年にしても同じ結果である。
ただし、1年観察期間として、1年生存率と読み替えて計算することになる。
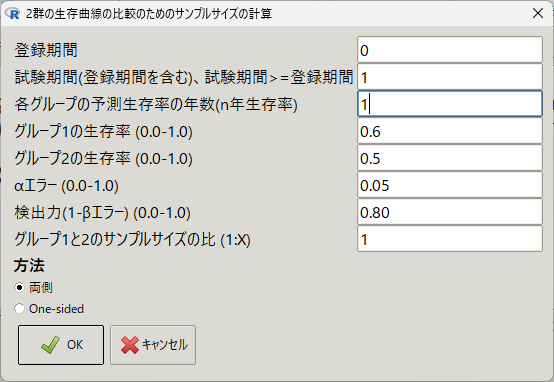
> SampleHazard(0, 1, 1, 0.6, 0.5, 0.05, 0.80, 2, 1)
仮定
P1 0.6
P2 0.5
P1、P2の観察期間 1
登録期間 0
全研究期間 1
αエラー 0.05
両側検定
検出力 0.8
N2とN1のサンプルサイズの比 1
必要サンプルサイズ 計算結果
N1 380
N2 380
5年観察で、治療群が0.8、コントロール群が0.3の場合、EZRで計算すると、以下の通り一群18例と計算された。
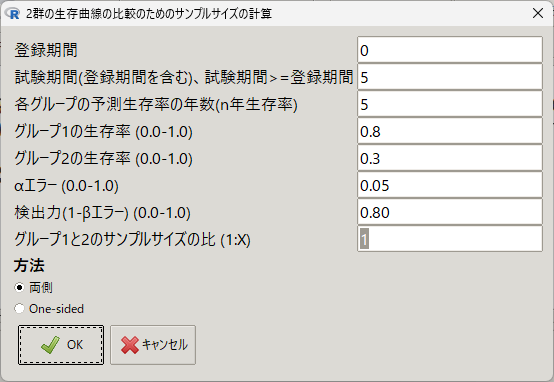
> SampleHazard(0, 5, 5, 0.8, 0.3, 0.05, 0.80, 2, 1)
仮定
P1 0.8
P2 0.3
P1、P2の観察期間 5
登録期間 0
全研究期間 5
αエラー 0.05
両側検定
検出力 0.8
N2とN1のサンプルサイズの比 1
必要サンプルサイズ 計算結果
N1 18
N2 18
登録期間を考慮したより適切な方法
後ろ向きの観察研究であっても、登録期間は設定できるし、試験期間も適切に設定できる。
登録期間は、全対象者の観察開始日を古い症例から新しい症例まで並べ替えて、もっとも古く登録された症例の日付からもっとも新しく登録された症例の日付までを使えば計算できる。
試験期間は、登録開始から、最後の登録症例の観察終了までの期間である。登録期間が長ければ、登録後の観察期間が短くなり、その分症例は多く必要になる。
上記の5年間の観察期間で、治療群が生存率 0.8 、コントロール群が生存率 0.65 と同じ条件で、登録期間を 2 年間としてみる。
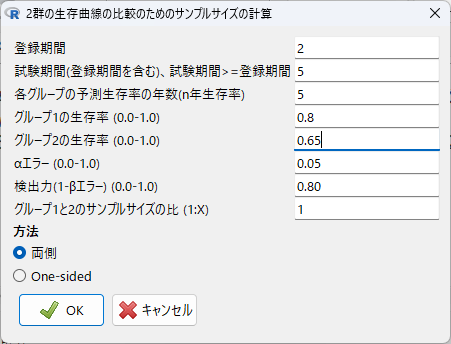
登録期間 0 年とした場合は、一群 141 例必要と計算されたが、登録期間を 2 年間とすると、一群 171 例必要と計算される。
> SampleHazard(2, 5, 5, 0.8, 0.65, 0.05, 0.80, 2, 1)
仮定
P1 0.8
P2 0.65
P1、P2の観察期間 5
登録期間 2
全研究期間 5
αエラー 0.05
両側検定
検出力 0.8
N2とN1のサンプルサイズの比 1
必要サンプルサイズ 計算結果
N1 171
N2 171登録期間 0 でいきなり全症例が登録されることはないため、現実的には、このように登録期間を適切に考慮した見積もりのほうがよい。
R のパッケージ powerSurvEpi を使った場合
まず Rに powerSurvEpi パッケージをインストールする。
install.packages("powerSurvEpi")
使うときは library() で呼び出す。
library(powerSurvEpi)
ssizeCT.default() という関数を使う。サンプルサイズ計算に必要な数値は以下の通り。
- power : 検出力
- k : 実験群(新薬群、実薬群など)と対照群(従来薬群、プラセボ群など)の比
- pE : 実験群のイベント発生割合
- pC : 対照群のイベント発生割合
- RR : ハザード比
- alpha : 有意水準(指定しなければ0.05)
治療群が生存率0.8、コントロール群が生存率0.65のとき、pE=1-0.8=0.2、pC=1-0.65=0.35である。
またハザード比は、log(0.8)/log(0.65)で計算できる。
この時一群142例と計算される。
Freedman式による計算だ。
> ssizeCT.default(power=0.8, k=1, pE=1-0.8, pC=1-0.65, RR=log(0.8)/log(0.65))
nE nC
142 142
治療群0.6、コントロール群0.5の場合は、pE=1-0.6=0.4, pC=1-0.5=0.5, RR=log(0.6)/log(0.5)である。
この時一群381例必要と計算される。
> ssizeCT.default(power=0.8, k=1, pE=0.4, pC=0.5, RR=log(0.6)/log(0.5))
nE nC
381 381
治療群が0.8、コントロール群が0.3の場合は、pE=1-0.8=0.2, pC=1-0.3=0.7, RR=log(0.8)/log(0.3)となり、一群19例必要と計算される。
> ssizeCT.default(power=0.8, k=1, pE=0.2, pC=0.7, RR=log(0.8)/log(0.3))
nE nC
19 19
Freedman 式か Schoenfeld 式か
Freedmanに比べて、Schoenfeldのほうが、小さいサンプルサイズでよいと計算される。
小さいサンプルサイズで済むならそれに越したことはない。
倫理的に最小人数が適切である。
しかし、Schoenfeldの式は、必要なイベント数を過小評価していると指摘されている。
結論として、比較的多くの症例を集めることが可能であれば、Freedman式の計算結果をお勧めする。
生存時間解析のサンプルサイズ計算をエクセルで
よければ以下からどうぞ。
コックス比例ハザードモデルのプルサイズ計算【エクセルでサンプルサイズ】Cox proportional hazard model sample size calculator | TKER SHOP
【解説動画】コックス比例ハザードモデルのサンプルサイズ計算
エクセルファイルの使い方動画を公開した。
よかったらどうぞ。
【解説動画】EZRでCoxのサンプルサイズ計算
EZRでは、登録期間を考慮できる。
こちらもよければ。
まとめ
生存時間解析のサンプルサイズ計算を Cox の比例ハザードモデルを前提に行う方法を解説した。
参考になれば。
参考書籍
医学統計学シリーズ3 Cox比例ハザードモデル 中村 剛 著 朝倉書店
3.8 必要sample sizeの計算法
参考文献
SASプロシジャを用いた生存時間データに対する例数設計の変革(PDF)
The asymptotic properties of nonparametric tests for comparing survival distributions
Tables of the number of patients required in clinical trials using the logrank test








コメント
コメント一覧 (2件)
[…] R EZR で生存時間解析のサンプルサイズ計算を行う方法 生存時間解析のサンプルサイズ計算の方法 Cox […]
[…] R と EZR で生存時間解析のサンプルサイズ計算を行う方法 生存時間解析のサンプルサイズ計算の方法 Cox […]