R と EZR で平均値の非劣性検定に必要なサンプルサイズを計算する方法

非劣性試験のエンドポイントが連続量で、各群の平均値を求める場合、サンプルサイズはどのように計算するか？

RとEZRで行う方法。

非劣性試験における非劣性検定とは？

劣っていないことを積極的に証明する検定。

臨床的に意味のある差を設定して、それよりは下回らないことを証明する。

詳しくはこちらを参照。

非劣性試験のサンプルサイズ計算　平均値の非劣性検定　1:1の場合

1:1、つまり、両群が同じ人数とする場合のサンプルサイズ計算が基本だ。

1:1の時がもっとも検出力が高くなり、両群合計が同じサンプルサイズなら統計学的有意になりやすい。

Deltaは、非劣性マージン。これ以上劣ったら、劣っているという限界。

Delta1は、非劣性が本当の場合の真実の差。

非劣性マージンの説明は以下に記載あり。

sample.size.non.inferiority.mean <- function(sig.level=.05, power=.8,
Delta, Delta1, sd, alternative="one.sided"){
alternative <- match.arg(alternative)
tside <- switch(alternative, one.sided=1, two.sided=2)
d <- (Delta + Delta1)/sd
Za <- qnorm(sig.level/tside, lower.tail=FALSE)
Zb <- qnorm(power)
n <- 2*((Za+Zb)/d)^2
NOTE <- "n is number in *each* group"
METHOD <- "Non Inferiority Test Sample Size Calculation (Mean)"
structure(list(n = n, "Non-inferiority margin" = Delta,
"True difference"=Delta1, SD = sd, sig.level = sig.level,
power = power, alternative = alternative, note = NOTE,
method = METHOD), class = "power.htest")
}

非劣性マージンが7、二群の差が34.5-29.7=4.8、標準偏差が30とする。

検出力80%、片側検定で有意水準5%の時、各群80例必要と計算される。

片側検定の理由も以下の記事に記載あり。

> sample.size.non.inferiority.mean(Delta=7, Delta1=34.5-29.7, sd=30)
Non Inferiority Test Sample Size Calculation (Mean)
n = 79.92389
Non-inferiority margin = 7
True difference = 4.8
SD = 30
sig.level = 0.05
power = 0.8
alternative = one.sided
NOTE: n is number in *each* group

非劣性試験のサンプルサイズ　平均値の非劣性検定　1:n の場合

1:nというのは、1:2とか1:3とか、どちらかの群を多くする場合。

集めるのが難しい群の人数を減らすとか、なるべく新しい治療法を多くの患者さんに割り当て従来の治療で比較対照にする群を少なくするとか、何らかの意図がある場合に用いる。

DeltaとDelta1は先ほどと同じ。

ctrl.ratioが 1:n の n の部分だ。

コントロールの比としているが、試験群でも使える。

スクリプトでは新治療が 1:n の1の群になっているので、異なる状況なら読み替えてほしい。

sample.size.non.inferiority.mean <- function(sig.level=.05, power=.8,
Delta, Delta1, sd, alternative="one.sided", ctrl.ratio=1){
alternative <- match.arg(alternative)
tside <- switch(alternative, one.sided=1, two.sided=2)
d <- (Delta + Delta1)/sd
Za <- qnorm(sig.level/tside, lower.tail=FALSE)
Zb <- qnorm(power)
n <- 2*((Za+Zb)/d)^2
m <- (ctrl.ratio+1)/(2*ctrl.ratio)*n
NOTE <- "n is number in *new treatment* group"
METHOD <- "Non Inferiority Test Sample Size Calculation (Mean)"
structure(
list("n (crude)" = ceiling(n), "n (corrected)" = ceiling(m), "n (corr. ctrl)" = ceiling(m * ctrl.ratio), "Total N (corrected)" = ceiling(m) + ceiling(m*ctrl.ratio),
"Control ratio" = ctrl.ratio,
"Non-inferiority margin" = Delta,
"True difference"=Delta1, SD = sd, sig.level = sig.level,
power = power, alternative = alternative, note = NOTE,
method = METHOD),
class = "power.htest")
}

1:1の時と同じ条件で計算したものが以下。

全部の群を計算させるために、各群の数字を整数に切り上げる関数を追加した。

切り上げておかないと、一例足らない数字に計算される可能性がある。

> sample.size.non.inferiority.mean(Delta=7, Delta1=34.5-29.7, sd=30)
Non Inferiority Test Sample Size Calculation (Mean)
n (crude) = 80
n (corrected) = 80
n (corr. ctrl) = 80
Total N (corrected) = 160
Control ratio = 1
Non-inferiority margin = 7
True difference = 4.8
SD = 30
sig.level = 0.05
power = 0.8
alternative = one.sided
NOTE: n is number in *new treatment* group

1:2とする場合のサンプルサイズは以下の通り。

1:1のときより、1:n の1の群は小さくなっている。

80例から60例に、20例減少している。

1:n の n の群は、1:2なので60の2倍の120必要になる。

全部で必要な人数は180例となって、1:1のときより20例余分に必要になる。

> sample.size.non.inferiority.mean(Delta=7, Delta1=34.5-29.7, sd=30, ctrl.ratio=2)
Non Inferiority Test Sample Size Calculation (Mean)
n (crude) = 80
n (corrected) = 60
n (corr. ctrl) = 120
Total N (corrected) = 180
Control ratio = 2
Non-inferiority margin = 7
True difference = 4.8
SD = 30
sig.level = 0.05
power = 0.8
alternative = one.sided
NOTE: n is number in *new treatment* group

非劣性試験のサンプルサイズ計算をEZRで実行してみる

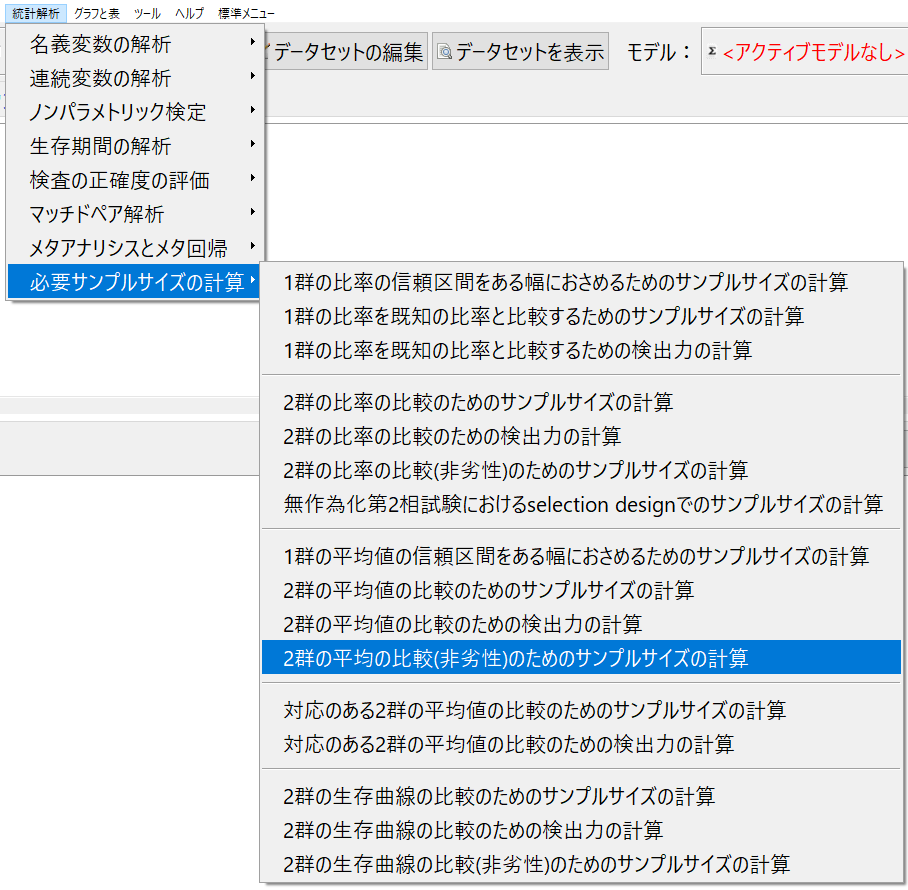
「統計解析」→「必要サンプルサイズの計算」→「2群の平均の比較（非劣性）のためのサンプルサイズの計算」を選択する。

2群の差が4.8、非劣性マージンが7、標準偏差が30、検出力80％、片側検定で有意水準5％の各値を入力する。

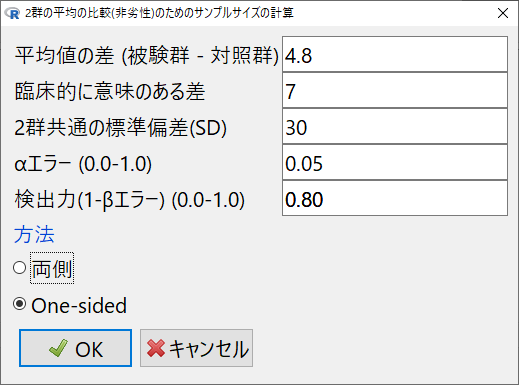
各設定値を入力する

各群80例必要と計算される。

> SampleMeanNonInf(4.8, 7, 30, 0.05, 0.80, 1)
仮定
2群間の平均値の差       4.8
意味のある差              7
標準偏差                 30
αエラー               0.05
片側検定
検出力                  0.8
必要サンプルサイズ 計算結果
N1                       80
N2                       80

1:2の場合など、2群が同数でない場合は、さらにRスクリプトに以下のように書いて実行する。例は1:2である。

n <- 80
ctrl.ratio <- 2
m <- (ctrl.ratio+1)/(2*ctrl.ratio)*n
(group1 <- m)
(group2 <- m*ctrl.ratio)

結果は、群1が60例、群2が120例と計算される。

> (group1 <- m)
[1] 60
> (group2 <- m*ctrl.ratio)
[1] 120

非劣性試験のサンプルサイズ計算をRのgsDesignパッケージのnNormal()関数を使って行う場合

gsDesign パッケージのnNormal()関数を使うと、平均値の非劣性検定のサンプルサイズ計算ができる。

EZRでも下記のとおりにインストール＆呼び出して、nNormal()関数を実行すれば、計算できる。

install.packages("gsDesign") #一回だけ
library(gsDesign) #gsDesignパッケージを使用時毎回、事前に一回だけ実行

nNormal()関数に条件を指定して実行すれば計算してくれる。非劣性マージンの符号がいままでと逆でマイナスになることに注意。

nNormal(delta1=4.8, delta0=-7, sd=30, alpha=0.05, beta=0.2) #1:1の場合
nNormal(delta1=4.8, delta0=-7, sd=30, alpha=0.05, beta=0.2, ratio=2) #1:2の場合

結果は、以下のように、1:1の場合は160例、1:2の場合は180例と計算される。

計算結果は2群合わせた合計の例数だ。

> nNormal(delta1=4.8, delta0=-7, sd=30, alpha=0.05, beta=0.2) #1:1の場合
[1] 159.8478
> nNormal(delta1=4.8, delta0=-7, sd=30, alpha=0.05, beta=0.2, ratio=2) #1:2の場合
[1] 179.8288

非劣性試験のサンプルサイズをエクセルで

よければ以下からどうぞ。

平均値の非劣性検定 サンプルサイズ計算【エクセルでサンプルサイズ】 | TKER SHOP

使い方動画。

こちらもよかったらどうぞ。

参考書籍