非劣性検定は劣っていないことを証明する検定。
割合の非劣性検定のサンプルサイズ計算はどうやるか?
割合の非劣性検定のサンプルサイズ計算
各変数の意味は、以下のとおりとする。
- pA:試験薬の有効率とする。
- pB:標準薬の有効率とする。
- pB.bar:帰無仮説H0: pA=pB-DELTAの下で推定されたpB.starの漸近値。
- DELTA:臨床的に意味のある最小の差。
片側5%、検出率80%を以下のスクリプトのデフォルト設定とする。
pAがpB-DELTAよりも大きいことを証明したいので、片側検定だ。
Rのスクリプトは以下の通り。
non.inferior.sample.size <- function(pA, pB, DELTA, power=.8, sig.level=.05, alternative="one.sided"){
alternative <- match.arg(alternative)
tside <- switch(alternative, one.sided = 1, two.sided = 2)
delta <- pA-pB
pB.bar <- pB+(delta+DELTA)/2
R <- sqrt((pB.bar-DELTA)*(1-pB.bar+DELTA)+pB.bar*(1-pB.bar))
S <- sqrt(pA*(1-pA)+pB*(1-pB))
Za <- qnorm(sig.level/tside, lower.tail=FALSE)
Zb <- qnorm(power)
n <- ((Za*R+Zb*S)/(delta+DELTA))^2
NOTE <- "n is number in *each* group"
METHOD <- "Non Inferiority Test Sample Size Calculation (Dunnett-Gent)"
structure(list(n = n, pA = pA, pB = pB, DELTA=DELTA, sig.level = sig.level,
power = power, alternative = alternative, note = NOTE,
method = METHOD), class = "power.htest")
}
RのスクリプトをRコンソールにコピペしてから、以下のようにして使う。
試験薬の有効率が0.813、標準薬の有効率が0.741、臨床的に有効な差が0.1、検出力90%で、必要サンプルサイズは各群100例必要と計算される。
> non.inferior.sample.size(pA=0.813, pB=0.741, DELTA=.1, power=.9)
Non Inferiority Test Sample Size Calculation (Dunnett-Gent)
n = 99.17305
pA = 0.813
pB = 0.741
DELTA = 0.1
sig.level = 0.05
power = 0.9
alternative = one.sided
NOTE: n is number in *each* group最尤推定量に基づく割合の非劣性検定のためのサンプルサイズ計算
各代数は前節と同じ。
Rスクリプトは以下の通り。
計算が少し複雑になるが、上記の計算式では対応できない条件の場合などにも対応できる。
例えば、上記の計算方法であると有効率 100 % のときは計算できない。
最尤推定量に基づく方法は、このような極端な割合に対しても対応可能である。
よって、いつでも、最尤推定量に基づく方法で計算するのが良い。
non.inferior.sample.size.likelihood <- function(pA, pB, DELTA, power=.8, sig.level=.05, alternative="one.sided"){
alternative <- match.arg(alternative)
tside <- switch(alternative, one.sided = 1, two.sided = 2)
delta <- pA-pB
a <- 2
b <- -2*pB-2-3*DELTA-delta
c <- DELTA^2+2*(1+pB)*DELTA+2*pB+delta
d <- -pB*DELTA*(1+DELTA)
v <- b^3/(27*a^3)-(b*c)/(6*a^2)+d/(2*a)
u <- sign(v)*sqrt(b^2/(9*a^2)-c/(3*a))
w <- (pi+acos(v/u^3))/3
pB.star <- 2*u*cos(w)-b/(3*a)
R <- sqrt((pB.star-DELTA)*(1-pB.star+DELTA)+pB.star*(1-pB.star))
S <- sqrt(pA*(1-pA)+pB*(1-pB))
Za <- qnorm(sig.level/tside, lower.tail=FALSE)
Zb <- qnorm(power)
n <- ((Za*R+Zb*S)/(delta+DELTA))^2
NOTE <- "n is number in *each* group"
METHOD <- "Non Inferiority Test Sample Size Calculation (Likelihood Method)"
structure(list(n = n, pA = pA, pB = pB, DELTA=DELTA, sig.level = sig.level,
power = power, alternative = alternative, note = NOTE,
method = METHOD), class = "power.htest")
}
前節より幾分必要サンプルサイズが大きくなり、各群102例必要と計算される。
> non.inferior.sample.size.likelihood(pA=0.813, pB=0.741, DELTA=.1, power=.9)
Non Inferiority Test Sample Size Calculation (Likelihood Method)
n = 101.4188
pA = 0.813
pB = 0.741
DELTA = 0.1
sig.level = 0.05
power = 0.9
alternative = one.sided
NOTE: n is number in *each* group非劣性試験のサンプルサイズ EZRで行う方法
「統計解析」→「必要サンプルサイズの計算」→「2群の比率の比較(非劣性)のためのサンプルサイズの計算」を選択。
必要な値を入力する。
対照群0.741、試験群0.813、非劣性マージン0.1、片側有意水準0.05、検出力90%とする。
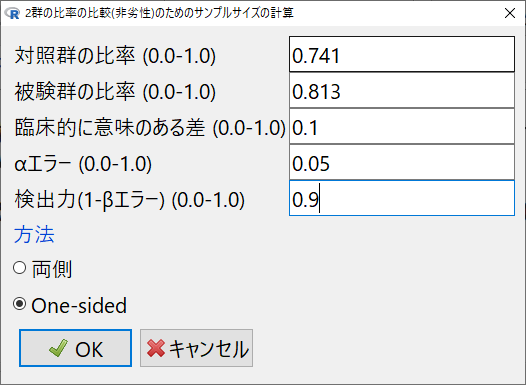
必要な値の入力
出力結果はこちら。
各群100例必要と計算される。
最初に紹介した方法と同じ結果になっているのがわかる。
> SampleProportionNonInf(0.741, 0.813, 0.1, 0.05, 0.9, 1)
仮定
P1 0.741
P2 0.813
意味のある差 0.1
αエラー 0.05
片側検定
検出力 0.9
必要サンプルサイズ 計算結果
N1 100
N2 100非劣性試験のサンプルサイズ RのgsDesignパッケージのnBinomial()関数で計算する方法
gsDesignパッケージをインストールして、library()で呼び出して使えるようにする。
EZRでもRスクリプト画面にコピペして実行すれば同じことができる。
install.packages("gsDesign") #一回だけ
library(gsDesign) #パッケージ使用時毎回、事前に一回実行
nBinomial()を使って計算する。
必要サンプルサイズの結果は、2群合わせての人数になっている。
最尤推定量に基づく方法と同じ結果である。
> nBinomial(p1 = 0.741, p2 = 0.813, delta0 = 0.1, alpha = 0.05, beta = 0.1)
[1] 202.8376
非劣性試験のサンプルサイズ エクセルで行う方法(最尤推定量に基づく方法)
よければ以下からどうぞ。
割合の非劣性検定 サンプルサイズ計算 (最尤推定量に基づく方法)【エクセルでサンプルサイズ】 | TKER SHOP
非劣性試験のサンプルサイズ 割合の非劣性検定 サンプルサイズ計算 エクセルファイルの使い方【動画】
エクセルファイルの使い方動画。
よければこちらもどうぞ。








コメント
コメント一覧 (1件)
[…] R と EZR で割合の非劣性検定に必要なサンプルサイズを計算する方法 非劣性検定は劣っていないことを証明する検定。 […]