トレンド検定のサンプルサイズ計算。
トレンド検定とは
トレンドとは、順序カテゴリの小さいほうから大きいほうに移るにつれて、カテゴリの平均値や割合が大きくなるとか小さくなるとか、傾向や相関があることを指す。
トレンドがなく同じというのが帰無仮説で、母集団で、だんだんに大きくなる、もしくは小さくなるトレンドがあるのかを、検定する。
トレンド検定 平均値の場合
母数とスコアの相関係数を考える。
ポイントは、合計が0になるようにスコアを与えること。
c: 線形対比(ベクトル)←これがポイント。
K=3(3グループ)の場合はc(-1,0,1)
K=4の場合はc(-3,-1,1,3):等間隔(間隔は2)
mu: 母平均(ベクトル)
sigma.sq: ANOVAから計算される誤差分散(下記分散分析表の太字下線部分)
| Df | Sum Sq | Mean Sq | F value | Pr(>F) | ||
|---|---|---|---|---|---|---|
| tension | 2 | 2034 | 1017.1 | 7.206 | 0.00175 | ** |
| Residuals | 51 | 7199 | 141.1 |
R スクリプトは以下の通り。
samplesize.mean.trend.test <- function(mu, sigma.sq, score, sig.level=.05, power=.8){
METHOD <- "Sample size determination for trend test of the means"
NOTE <- "n is each number in groups"
Za <- qnorm(sig.level/2, lower.tail=FALSE)
Zb <- qnorm(power)
n <- ((Za+Zb)^2 * sigma.sq * sum(score^2))/(sum(score*mu)^2)
structure(list(n=n, mu=mu, sigma.sq=sigma.sq, score=score, sig.level=sig.level, power=power, method=METHOD, note=NOTE), class = "power.htest")
}
平均値のトレンド検定サンプルサイズ計算 例1
参考書籍の例題は、以下のように計算される。
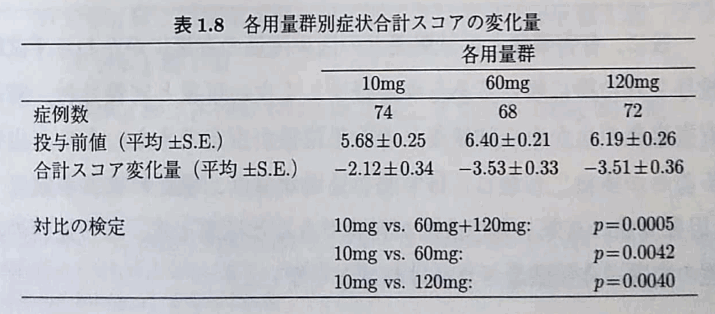
例題は分散分析表でなくSE(標準誤差)の値がわかるタイプ。
症状スコアの変化量は、-2, -3.5, -3.5と想定されるとする。
相関を見る線形対比は-2, 1, 1とする。
合計でゼロになるようにすることと、
症状スコアの変化量を表している数字にすること。
三群のうち、-2の群だけ違うわけなので、
その場合は-2, 1, 1というスコアが妥当。
(変化量と割り当てるスコアがともに-2なのはたまたま。念のため)
誤差分散は最大のSE=0.36の二乗に三群の症例数の真ん中あたり70例をかける。
SEはこんなふうに計算される。
$$ SE = \sqrt{\frac{分散}{n}} $$
よって二乗して症例数をかけると分散に戻る。
$$ \left( \sqrt{\frac{分散}{n}} \right)^2 \times n = \frac{分散}{n} \times n = 分散 $$
結果として一群48例必要と計算される。
> samplesize.mean.trend.test(mu=c(-2,-3.5,-3.5), sigma.sq=70*0.36^2, score=c(-2,1,1))
Sample size determination for trend test of the means
n = 47.47002
mu = -2.0, -3.5, -3.5
sigma.sq = 9.072
score = -2, 1, 1
sig.level = 0.05
power = 0.8
NOTE: n is each number in groups
平均値のトレンド検定サンプルサイズ計算 例2
もう一つの例として、warpbreaksデータセットで計算してみる。
warpbreaksのデータでトレンド検定してみた結果は以下を参照(リンク先記事の最下段)。
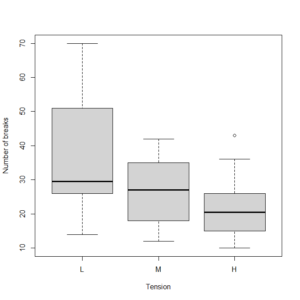
各群の平均値は、以下のように、36.4, 26.4, 21.7とする。
> with(data=warpbreaks, tapply(breaks, tension, mean))
L M H
36.38889 26.38889 21.66667
また、誤差分散は分散分析表から141.1とする。
> aov.res <- aov(breaks ~ tension, data=warpbreaks)
> summary(aov.res)
Df Sum Sq Mean Sq F value Pr(>F)
tension 2 2034 1017.1 7.206 0.00175 **
Residuals 51 7199 141.1
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1
上記の条件で計算すると、各群11例必要と計算される。
実際のデータは各群18例なので、
トレンド検定のためには少し多めだが悪くはない。
> samplesize.mean.trend.test(mu=c(36.4, 26.4, 21.7), sigma.sq=141.1, score=c(1,0,-1))
Sample size determination for trend test of the means
n = 10.25015
mu = 36.4, 26.4, 21.7
sigma.sq = 141.1
score = 1, 0, -1
sig.level = 0.05
power = 0.8
NOTE: n is each number in groups
トレンド検定のサンプルサイズ計算 平均値の場合をエクセルで
よければ、下記のリンク先からどうぞ。
5グループまで対応。
平均値のトレンド検定 サンプルサイズ計算【エクセルでサンプルサイズ】 | TKER SHOP
使い方解説動画。
こちらもよければどうぞ。
トレンド検定 割合の場合
R スクリプトは以下の通り。
割合のベクトルはprop、線形対比ベクトルはscore、でそれぞれインプットする。
samplesize.prop.trend.test <- function(prop, score, sig.level=.05, power=.8){
METHOD <- "Sample size determination for trend test of the proportions"
NOTE <- "n is each number in groups"
p <- mean(prop)
R <- sqrt(p*(1-p)*sum(score^2))
S <- sqrt(sum(score^2*prop*(1-prop)))
Za <- qnorm(sig.level/2, lower.tail=FALSE)
Zb <- qnorm(power)
n <- ((Za*R+Zb*S)/sum(score*prop))^2
structure(list(n=n, proportion=prop, score=score, sig.level=sig.level, power=power, method=METHOD, note=NOTE), class = "power.htest")
}
割合のトレンド検定サンプルサイズ計算 例1
例えば有効率が55%、75%、75%の三群と予想できるとする。
線形対比スコアは平均値の時と同じ-2, 1, 1とする。
55%の群だけ有効性が低いと見えるからだ。
このときにトレンド検定で有意になるには各群65例必要と計算される。
> samplesize.prop.trend.test(prop=c(0.55,0.75,0.75), score=c(-2,1,1))
Sample size determination for trend test of the proportions
n = 64.66423
proportion = 0.55, 0.75, 0.75
score = -2, 1, 1
sig.level = 0.05
power = 0.8
NOTE: n is each number in groups
割合のトレンド検定サンプルサイズ計算 例2
もう一つ、carDataパッケージのTitanicSurvivalというデータで検証してみよう。
carDataパッケージは最初からインストールされているので、呼び出すだけで使えるようになる。
タイタニック号が沈没したとき生存した乗客の性別、年齢、客室クラスのデータ。
客室クラスで生存割合にトレンドがあるかどうかを見てみる。
割合のトレンド検定はCochran-Armitage検定で、prop.trend.test()でできる。
以下の過去記事も参照。

library(carData)
with(TitanicSurvival, table(passengerClass, survived))
tab <- with(TitanicSurvival, table(passengerClass, survived))
prop.table(tab,1)
prop.table(tab,1)[,2]*100
barplot(prop.table(tab,1)[,2]*100, xlab="Passenger Class", ylab="Survived (%)")
prop.trend.test(tab[,2], rowSums(tab), score=c(1,0,-1))
生存割合は、一等が62%、二等が43%、三等が26%だった。
グラフにすると見事にトレンドがみられる。
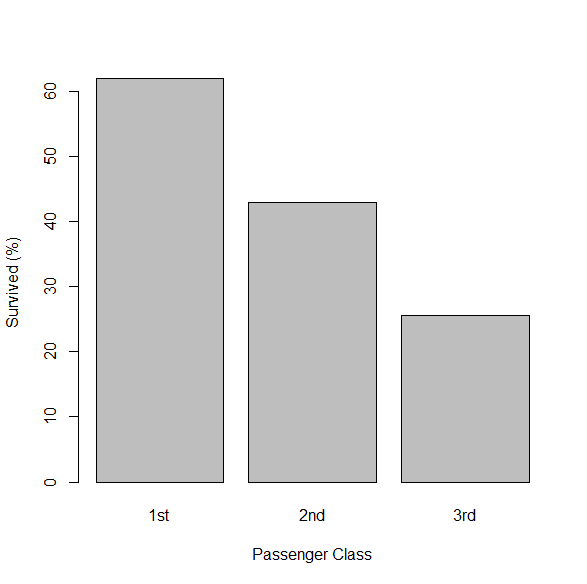
タイタニック号事故 客室クラスと生存割合
結果は統計学的有意でトレンドあり。
> library(carData)
>
> with(TitanicSurvival, table(passengerClass, survived))
survived
passengerClass no yes
1st 123 200
2nd 158 119
3rd 528 181
>
> tab <- with(TitanicSurvival, table(passengerClass, survived))
>
> prop.table(tab,1)
survived
passengerClass no yes
1st 0.3808050 0.6191950
2nd 0.5703971 0.4296029
3rd 0.7447109 0.2552891
>
> prop.table(tab,1)[,2]*100
1st 2nd 3rd
61.91950 42.96029 25.52891
>
> barplot(prop.table(tab,1)[,2]*100, xlab="Passenger Class", ylab="Survived (%)")
>
> prop.trend.test(tab[,2], rowSums(tab), score=c(1,0,-1))
Chi-squared Test for Trend in Proportions
data: tab[, 2] out of rowSums(tab) ,
using scores: 1 0 -1
X-squared = 127.81, df = 1, p-value < 2.2e-16
もし仮にサンプルサイズ計算をすると、一群29例と計算される。
タイタニックは試験ではなく悲劇の事故なので、サンプルサイズ計算の対象ではないが、もしもの話なので、あしからず。
> samplesize.prop.trend.test(prop=c(0.62,0.43,0.26), score=c(1,0,-1))
Sample size determination for trend test of the proportions
n = 28.603
proportion = 0.62, 0.43, 0.26
score = 1, 0, -1
sig.level = 0.05
power = 0.8
NOTE: n is each number in groups
トレンド検定のサンプルサイズ計算 割合の場合をエクセルで
よければ、下記のリンク先からどうぞ。
5グループまで対応。
割合のトレンド検定 サンプルサイズ計算【エクセルでサンプルサイズ】 | TKER SHOP
使い方解説動画。
こちらもよければどうぞ。
まとめ
トレンド検定のサンプルサイズ計算を、平均値の場合と割合の場合に分けて紹介した。
三群以上で、群間比較は不要で、トレンドだけ見られればいいという状況は少ないと思うが、もし必要な場合はこの記事のスクリプトを使えば計算できる。
参考書籍
出典:丹後俊郎著 無作為化比較試験 朝倉書店
3.7 傾向性検定-量反応関係の検出










コメント