IPTW カプランマイヤー曲線の書き方。
RのパッケージとEZRを使うと書ける。
IPTWとは?
IPTW とは、Inverse Probability of Treatment Weights の頭文字語。
逆確率重み付けの意味。
傾向スコア (Propensity Score) を使った、交絡要因調整の一種。
処方されにくい分画に、処方意向確率 (Propensity Scoreと呼ばれる) の逆数で重みを付けて、処方されやすい分画とバランスをとって、比較可能性を上げる方法。
IPTW カプランマイヤー曲線とは?
IPTWでバランスをった上での群間比較カプランマイヤー曲線のこと。
これを書くにはどうすればよいか?
RでIPTW カプランマイヤー曲線を書く方法
RISCAパッケージのインストール
RISCAパッケージをインストールして、ipw.survival() が使えるようにする。
install.packages("RISCA")
library(RISCA)
いくつかパッケージの更新が必要になる場合があるので、根気よく一つずつ更新する。
Rコンソールメニューの「パッケージ」→「パッケージの更新」を使うと更新できる。
以下のリンク先のRスクリプトが必要な ipw.survivial() 関数なので、これをコンソールにコピペしてインストールの代わりにしてもよい。
RISCA source: R/ipw.survival.R
EZRでIPTWを作成する
EZRのロジスティック回帰分析のメニューを借りて、IPTWの変数を作成する。
処方の有無(背景をなるべく揃えたい因子)を目的変数にして、その処方に影響を与える因子で説明するロジスティック回帰モデルを作成し、IPTWを計算する。
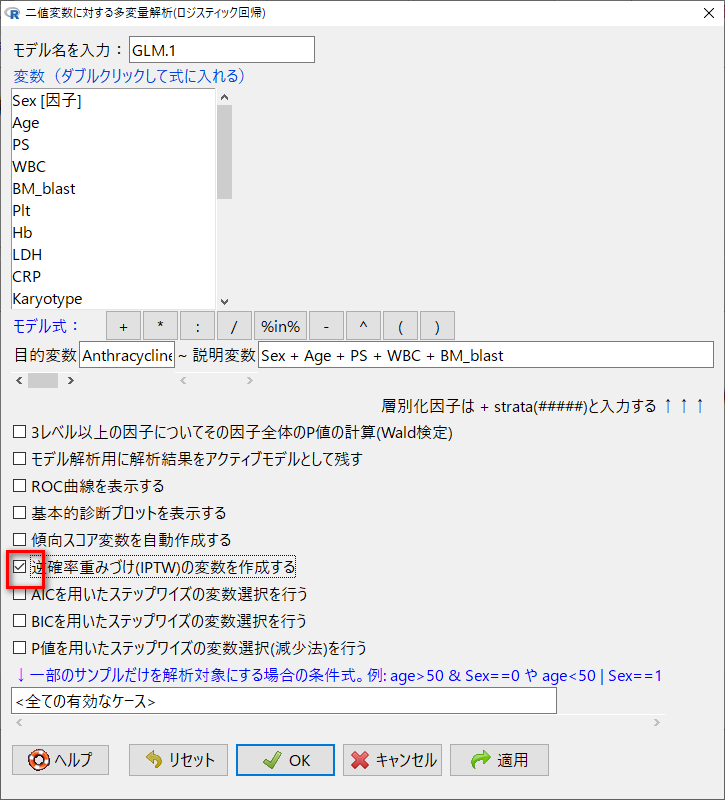
赤枠のチェックがIPTW作成のための指定箇所である。
OKを押して計算すると、weight.ATE.GLM.1という変数が作成される。
これがIPTWである。
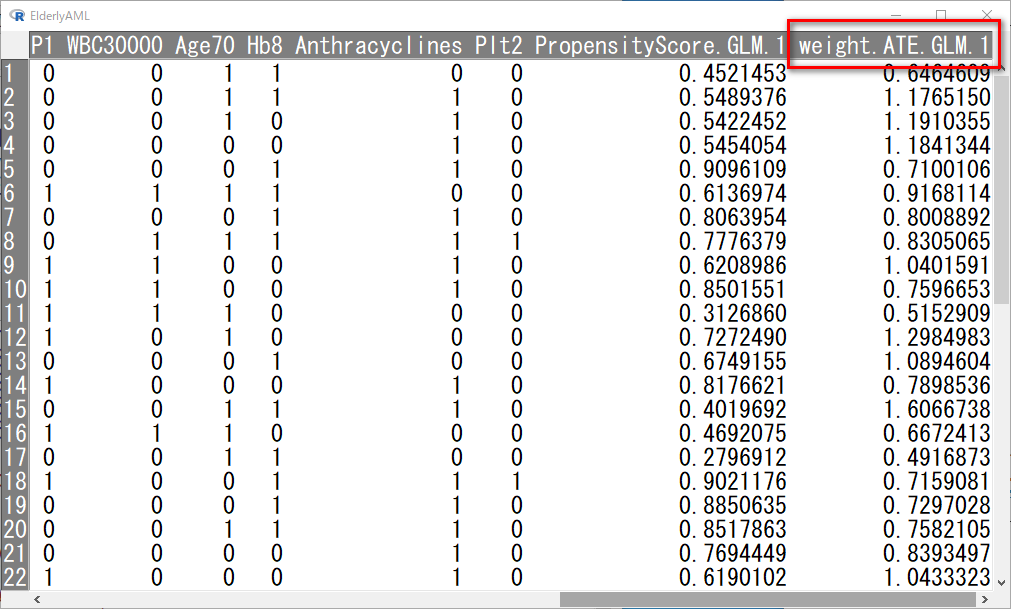
ここまで準備して、ipw.survival() 関数に戻る。
ipw.survival関数でIPTW 生存確率を計算する
RコンソールでもEZRのRスクリプト窓でもよいので、以下のように書いて実行すると、IPTW カプランマイヤー生存曲線のための数値が計算できる。
この関数では IPTW を IPW と表現しているので注意。
IPTW と IPW は同じものを指している。
res <- with(ElderlyAML, ipw.survival(times = Days,
failures = Survival, variable = Anthracyclines,
weights = weight.ATE.GLM.1))
欠損があると計算されないので、あらかじめ欠損があるケースは削除する処理を行っておく。
解析結果を少し見てみると、以下のような構造になっている。
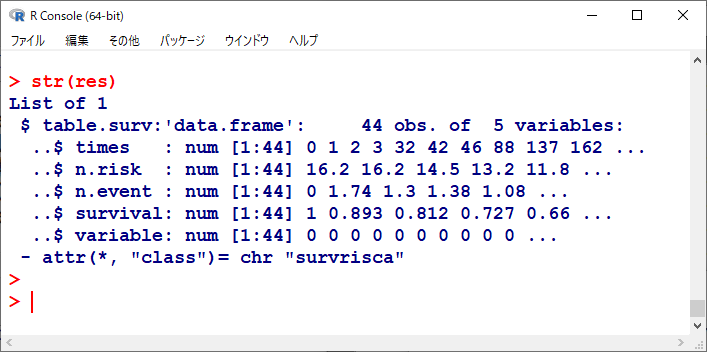
times は生存時間、n.risk は number at risk、n.event は number of events、survival は IPTW カプランマイヤー生存確率、variable は群分け変数である。
n.risk と n.event が小数まであり、IPTWがかかっていることがわかる。
あとはこのデータをグラフに書くのみである。
IPTWカプランマイヤー曲線を書く
まず、空白のグラフ範囲を作成する。
plot(NULL, xlim=c(0,2100), ylim=c(0,1), ylab="Survival",
xlab="Time")
X軸の範囲はあらかじめ調べておくとよい。
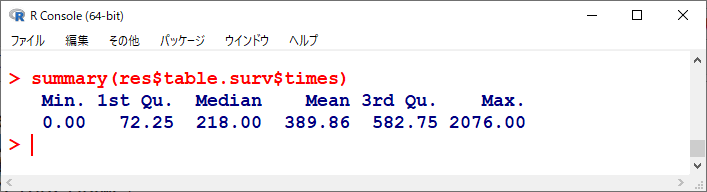
一本目は処方あり variable == 1 の線を書く。
lines(x = res$table.surv$times[res$table.surv$variable==1],
y = res$table.surv$survival[res$table.surv$variable==1],
type = "s", col=1)
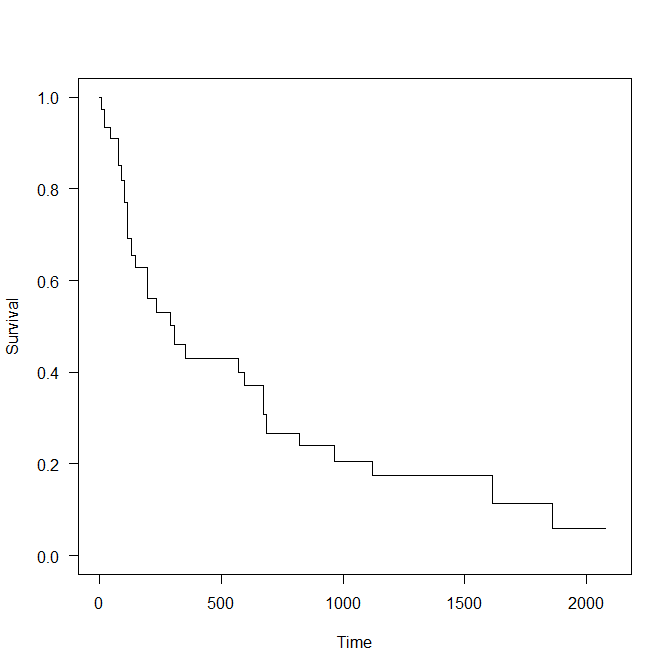
二本目は、処方なしで生存確率が速く下がってしまう variable == 0 を書く。
lines(x = res$table.surv$times[res$table.surv$variable==0],
y = res$table.surv$survival[res$table.surv$variable==0],
type = "s", col=2)
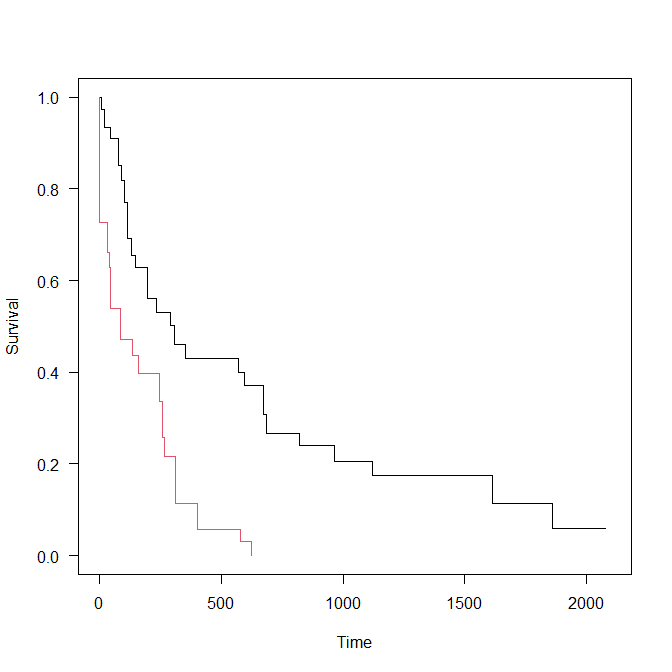
最後に、右上のほうに Legend を挿入して完成である。
legend("topright", legend=c("Anthracyclines Treated",
"Anthracyclines Untreated"), col=c(1,2), lty=c(1,1))
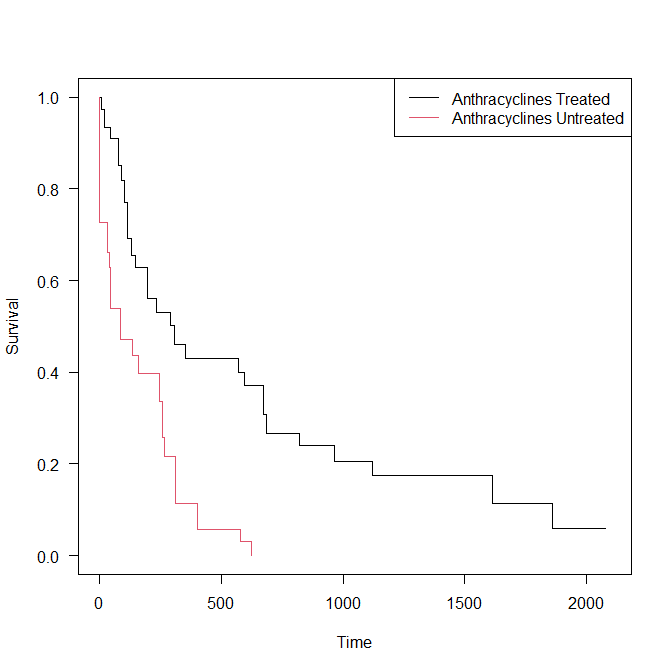
IPTWで重み付けをしていないカプランマイヤー曲線を書いてみると以下のとおりである。
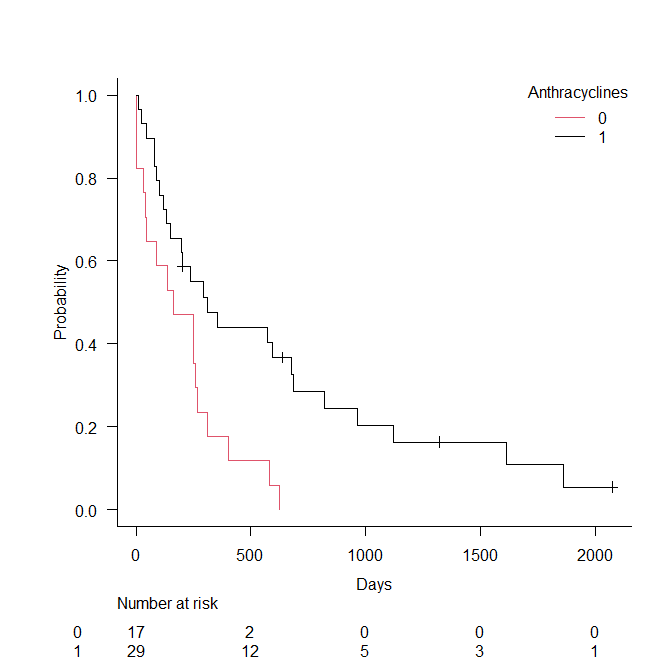
黒の線はあまり変わっていないが、赤の線が若干変わっているのがわかる。
生存確率0.4あたりのイベントの起き方が異なっているように見える。
このようにIPTWで重み付けをしたカプランマイヤー曲線は、重み付けなしの曲線とは若干異なる曲線になるわけである。
実は、もっと簡単に書ける。
あとになって気づいた。
### plot.survrisca
plot(res, col=2:1,
xlab='Time', ylab='Survival')
legend("topright", legend=c("Anthracyclines Treated",
"Anthracyclines Untreated"),
col=c(1,2), lty=c(1,1))
このようにスクリプトを書くだけで、以下のグラフが描ける。
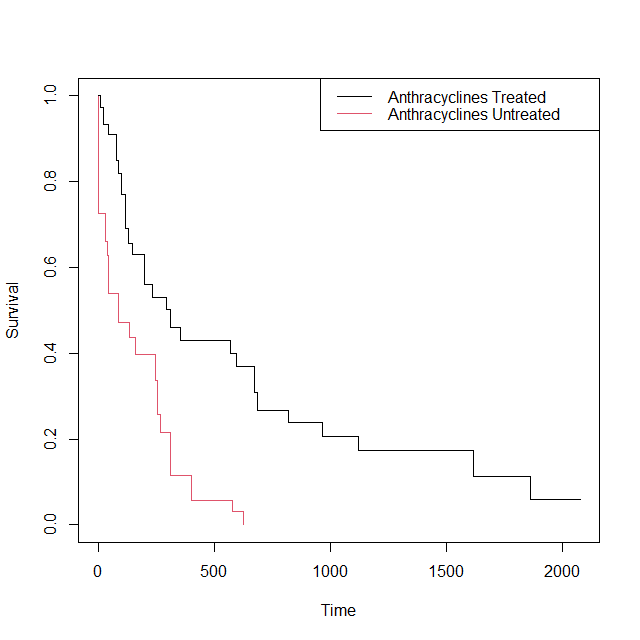
打ち切りマークを入れた IPTW KM 曲線の書き方
打ち切りが発生したところに縦線を付けたい場合は、違うパッケージを使うとできる。
adjustedCurves というパッケージを使う。
関数は、adjustedsurv() である。
library(adjustedCurves)
library(survival)
library(ggplot2)
### 群別の変数を因子に
ElderlyAML$Anthracyclines.Factor <-
as.factor(ElderlyAML$Anthracyclines)
### 傾向スコア計算のためのロジスティック回帰
GLM.1 <- glm(Anthracyclines ~
Sex + Age + PS + WBC + BM_blast,
family=binomial(logit), data=ElderlyAML)
### iptw_km を指定して、傾向スコア計算モデルも指定する
adjsurv <- adjustedsurv(data=ElderlyAML,
variable='Anthracyclines.Factor',
ev_time='Days', event='Survival',
method='iptw_km',
treatment_model=GLM.1)
### censoring_ind='lines' で打ち切り例発生時点に線が引ける
plot(adjsurv, censoring_ind='lines')
以下のようなグラフになる
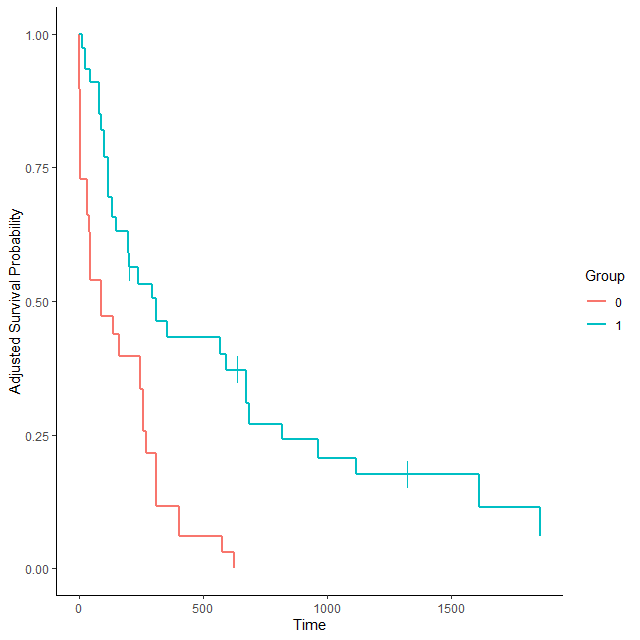
EZR などで別途作成した IPTW を使用することもできる
weight.ATE.GLM.1 という変数名の IPTW を treatment_model で指定する
### iptw_km を指定して、計算済みの IPTW を指定する
adjsurv <- adjustedsurv(data=ElderlyAML,
variable='Anthracyclines.Factor',
ev_time='Days', event='Survival',
method='iptw_km',
treatment_model=ElderlyAML$weight.ATE.GLM.1)
### censoring_ind='lines' で打ち切り例発生時点に線が引ける
plot(adjsurv, censoring_ind='lines')
そうすると以下のようにグラフが書ける
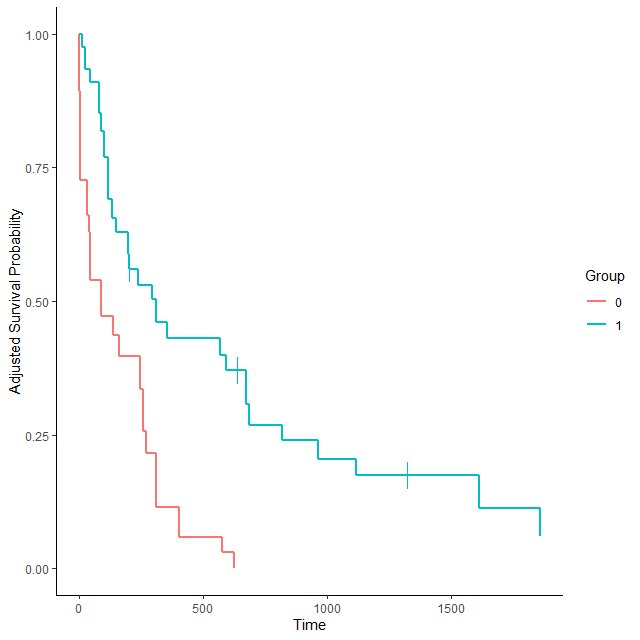
IPTW 累積発生率曲線の書き方
累積発生率は、生存率を 1 から引けばよいので、y = 1 – res$ … とすればよい。
plot(NULL, xlim=c(0,2100), ylim=c(0,1),
ylab="Cumulative Incidence", xlab="Time")
lines(x = res$table.surv$times[res$table.surv$variable==1],
y = 1-res$table.surv$survival[res$table.surv$variable==1],
type = "s", col=1)
lines(x = res$table.surv$times[res$table.surv$variable==0],
y = 1-res$table.surv$survival[res$table.surv$variable==0],
type = "s", col=2)
legend("bottomright", legend=c("Anthracyclines Treated",
"Anthracyclines Untreated"), col=c(1,2), lty=c(1,1))
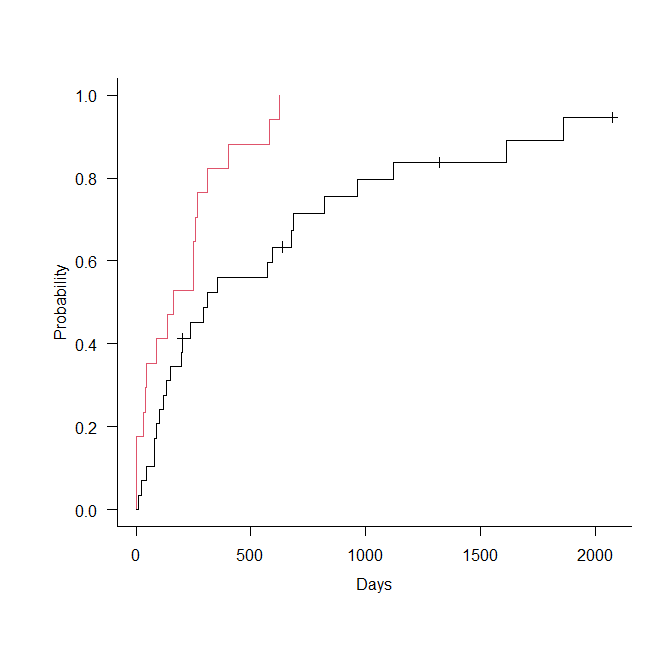
すると、以下のように生存率を逆さにしたグラフが描ける。
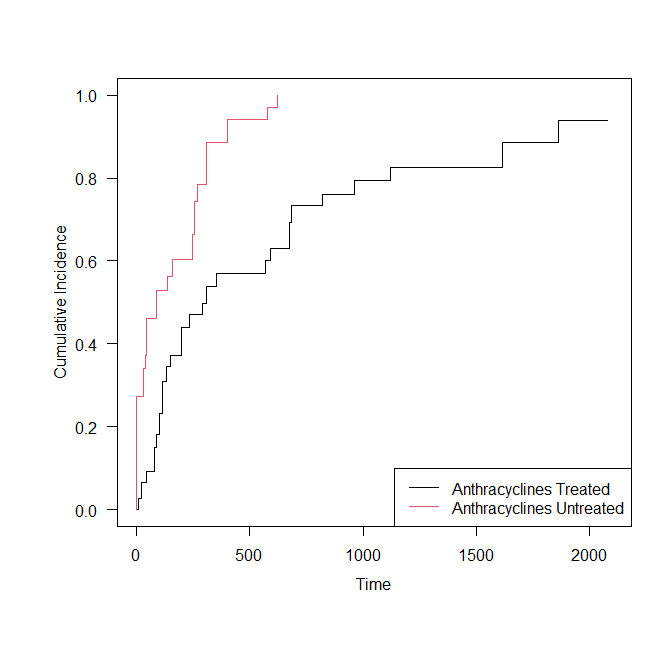
通常のカプランマイヤー曲線も、plot(km, …) とあるスクリプトに、fun = ‘event’ と加筆するだけで、累積発生率の曲線が書ける。
まとめ
統計ソフトRで、RISCA パッケージの ipw.survival() 関数を用いた、IPTWカプランマイヤー曲線を書いてみた。
EZRのロジスティック回帰分析のメニューを借りると簡単にIPTWが計算できるので、EZRの力を借りるのがおすすめ。
あとは、少しだけRスクリプトを書かないといけないが、上記を参考に、変数名以外はコピペでOKなので、ぜひ試してみてほしい。
参考サイト
IPWsurvival パッケージを用いた統計的因果推論 x 生存分析 – YuRAN-HIKO
おすすめ書籍
EZR公式マニュアル






コメント
コメント一覧 (8件)
ありがとうございます。大変勉強になります。もし可能であれば
① IPTW-adjusted log-rank test
② 競合リスクを考慮したIPTW-adjusted cumulative incidence curveの描き方、
③ IPTW-adjusted Gray’s test (これはないのかもしれませんが)
もご教授頂けますと幸いです。
お返事遅くなりました。
①のIPTW ログランク検定は以下の記事にまとめましたので、ご覧ください。
https://toukeier.hatenablog.com/entry/IPTW-log-rank-test-using-EZR-and-R
②③は検討しまして、またブログにまとめたいと思います。
ありがとうございます。できるようになりたいと考えていたので、大変有難いです。
②については、以下の文献のFigure 2にIPTW-adjusted cumulative incidence curveがあり、自分もできるようになりたいと思っていたので、ご質問させて頂きました。。
J Clin Med. 2022 Aug 8;11(15):4618. doi: 10.3390/jcm11154618(PMID: 35956232)
③にあたるものは存在しないのかもしれないので、その場合は大変申し訳ありません。
大変時間がかかってしまいましたが、② 競合リスクを考慮したIPTW-adjusted cumulative incidence curveの描き方、について、ブログにまとめましたので、ご連絡いたします https://toukeier.hatenablog.com/entry/iptw-weighted-cumulative-incidence-curve-in-r
③の IPTW Gray 検定については、存在するかも含めて調査して、またご連絡いたします
[…] ↑1万人以上… あわせて読みたい R と EZR で IPTW カプランマイヤー曲線を書く方法 IPTW カプランマイヤー曲線の書き方。 […]
[…] R と EZR で IPTW カプランマイヤー曲線を書く方法 IPTW カプランマイヤー曲線の書き方。 […]
[…] R と EZR で IPTW カプランマイヤー曲線を書く方法 IPTW カプランマイヤー曲線の書き方。 […]
[…] 重回帰で用いる方法。 逆確率重み… あわせて読みたい R と EZR で IPTW カプランマイヤー曲線を書く方法 IPTW カプランマイヤー曲線の書き方。 […]