EZRで回帰直線のグラフに95%信頼区間を付ける方法
回帰直線を書くために EZRで線形回帰(単回帰)を実行する
まずEZRで単回帰を実行する。
例えば、以下のような感じに R スクリプト窓に出力される。
#####線形回帰(単回帰、重回帰)#####
library(aod, pos=18)
RegModel.1 <- lm(LogCD34perBW~WBC.entry, data=GCSF_CD34)
新しい独立変数を作成する
新しい独立変数 newx を作成する。
R スクリプト窓に以下を書く。
newx <- data.frame(WBC.entry=
seq(min(GCSF_CD34$WBC.entry), max(GCSF_CD34$WBC.entry),
length=200))
先ほどの単回帰で使った変数 WBC.entry の最小値から最大値までを200に区切った変数を作成している。
欠損値があると変数が作成できないので、欠損値がある行は削除してから作成する。
単回帰モデルと新しい独立変数で予測値・予測信頼区間を計算する
先ほどの単回帰のモデル RegModel.1 を使って、新しい独立変数 newx に対する予測信頼区間を計算する。
特に指定しなければ、95%信頼区間が計算される。
confint <- predict(RegModel.1, newx, interval="confidence")
confintは、200行3列の行列になる。
> str(confint)
num [1:200, 1:3] 0.0412 0.0441 0.047 0.0499 0.0528 ...
- attr(*, "dimnames")=List of 2
..$ : chr [1:200] "1" "2" "3" "4" ...
..$ : chr [1:3] "fit" "lwr" "upr"
fit, lwr, uprの3列だが、fitは推定値、lwrは信頼区間下限値、uprは信頼区間上限値である。
plot()で散布図を描きmatlines()で回帰直線と信頼区間の下限・上限を描き入れる
回帰直線の土台として、散布図を書く。
散布図を書くには、plot()を使う。
plot(LogCD34perBW ~ WBC.entry, data=GCSF_CD34)
~(チルダ)の左がY軸の値、右がX軸の値だ。
書かれた散布図がこちら↓
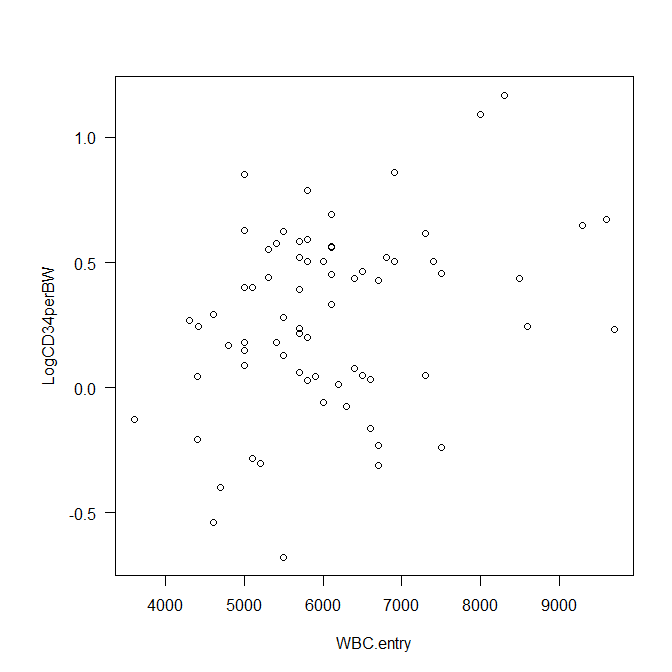
回帰直線 fit、信頼区間下限 lwr、信頼区間上限 upr、の3本の線をいっぺんに描かせられるのがmatlines()である。
matlines(newx, confint, col=1, lty=c(1,2,2))
X軸は newx, Y軸は confint を指定する。
col=1 は色の指定で、1は黒である。
ltyは線の種類で、1が実線、2が破線になる。
こんなふうに描ける。
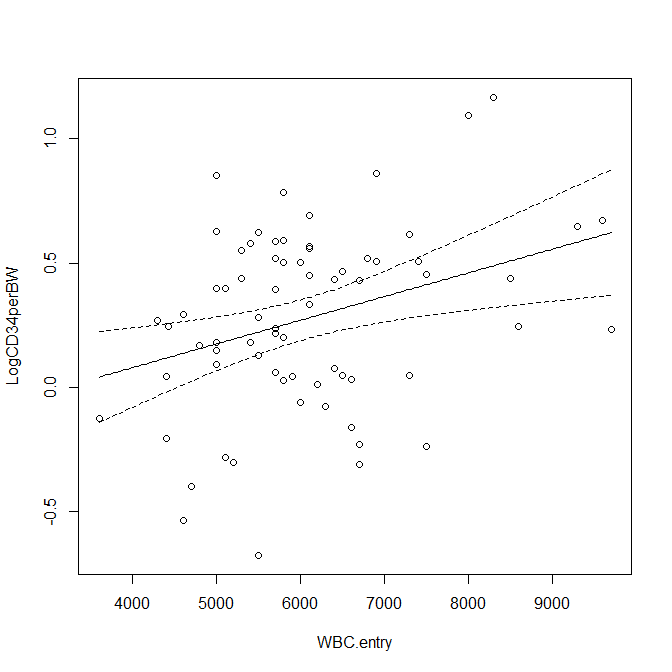
まとめ
EZRで散布図に回帰直線を描き入れて、さらに95%信頼区間を付ける方法を紹介した。
plot()で散布図を描いて、predict()で推定した回帰直線と信頼区間上限・下限をmatlines()で描かせる方法。
参考になれば。
参考PDF
中澤先生 R演習本 91ページ目
https://minato.sip21c.org/msb/medstatbookx.pdf
おすすめ書籍








コメント