実験や分析でデータを得た際、「検出限界以下(Not Detected: ND)」という結果に直面したことがあるだろう。これは、物質が存在する可能性はあっても、測定機器では捉えられなかったことを意味する。
これらの「見えない値」を無視して「0」と入力したり、適当な値に置き換えたりすると、データ分析の結果が大きく歪んでしまうことがある。
本記事では、初心者にも理解できるように、検出限界以下の値(Non-detects)がなぜ問題なのか、そして統計学的に最も信頼性の高い対処法を、わかりやすく解説する。
はじめに:検出限界以下の値が「厄介」な理由
分析や測定の世界には、機器の性能上の限界を示す3つの重要な概念がある。
- 感度:機器がわずかな変化を捉える能力である。
- 検出限界(LOD: Limit of Detection):物質がそこに「ある」ことを確認できる最小の量である。これ以下の値は「存在するかどうか」すら保証できない。
- 測定限界(LOQ: Limit of Quantitation):物質が「どれだけあるか」を正確に定量できる最小の量である。精度と正確さをもって「量」を議論できるラインである。
なぜ、これらの値以下が問題なのか?
検出限界以下(NDs)の値を安易に扱うと、分析結果の信頼性を損なう「バイアス(偏り)」が生じる。
| 処理方法 | データの歪み(バイアス) | 分散への影響 |
| NDsを「0」として代入 | 真の平均値を過小評価(負のバイアス) | データのばらつきを過小評価 |
| NDsを「LOD」として代入 | 真の平均値を過大評価(正のバイアス) | データのばらつきを過小評価 |
例えば、有害物質の平均濃度を調べるときに、本来は少し存在するNDsをすべて「0」とすると、「平均は安全なレベルだ」という誤った結論を導きかねない。
対処方法:NDsを乗り越える3つのアプローチ
検出限界以下の値を統計的に処理する方法は、大きく3つに分けられる。
① シンプルだが非推奨:代入法(Substitution)
| 代入する値 | 説明 |
| LOD/2 (検出限界の半分) | 最もよく使われる代入値であり、LODと0の中間をとる。 |
| LOD/ $\sqrt{2}$ | 統計的な研究で、分散の過小評価を最小限に抑えられると提案されている値である。 |
⚠️ 注意点: 代入法は、データにない値を勝手に入れているため、統計学的には最も正確ではない。NDsの割合が5%未満と非常に少ない場合に、やむを得ず使用される程度に留めるべきである。
② 分布を活かす:最大尤度推定(MLE)
これは最も推奨される統計的な方法である。
「打ち切りデータ(Censored Data)」という考え方を使う。NDsは「0からLODまでのどこかに存在する」という情報(範囲)を持つデータとして扱う。
- 仕組み:データ全体が特定の分布(例:対数正規分布)に従うと仮定し、その分布の中で、NDsが最もらしい平均値と標準偏差を数学的に推定する。
- メリット:代入法に比べてバイアスが極めて少なく、NDsの割合が高くても(例えば50%未満)、比較的正確な推定が可能である。
最大尤度推定(MLE)とは?データの「最もらしい」姿を探る統計の強力なツール
最大尤度推定(Maximum Likelihood Estimation, MLE)は、統計学において「データが最もよく説明されるような、母集団のパラメーター(平均や分散など)を推定する」ための非常に強力な手法である。
これは、観測されたデータ(手元にある実際の測定値)が、ある確率分布から生じたと仮定したとき、その「確率分布のパラメーターがどのような値であれば、このデータが観測される確率(尤度)が最大になるか」を追求する方法である。簡単に言えば、「もし母集団がこんな性質を持っていたら、目の前のデータが偶然出てくるはずがない。だから、母集団の性質はこうだったに違いない」と最もらしい値を逆算するアプローチだ。
検出限界以下の値(NDs)への応用
特に、検出限界以下の値(NDs)を扱う場合、MLEはその真価を発揮する。代入法のように「NDsをLOD/2」といった恣意的な値に置き換えるのではなく、NDsを「LOD以下のどこかに存在する、打ち切りデータ」として扱う。
MLEは、定量値(はっきり測定できた値)と、打ち切り情報(LOD以下という範囲の情報)の両方を同時に利用する。特定の分布(例:対数正規分布)を仮定し、この分布の平均と分散がどのような値であれば、「定量値が観測され、かつNDsがLOD以下に収まる」という複合的な事象の確率(尤度)が最大になるかを計算によって導き出す。
この方法により、NDsの割合が高くても、データ全体に最もフィットする母集団のパラメーターを推定できるため、バイアスを最小限に抑え、より信頼性の高い結論を得ることが可能となる。MLEは、代入法に比べて計算は複雑になるが、統計的な厳密さを求める分析において、最も推奨される標準的な手法の一つである。
③ 分布に頼らない:ノンパラメトリック法
特定の分布(正規分布など)を仮定せずにデータ分析を行う方法である。
- 利用場面:主にグループ間の比較(例:処理Aと処理Bの平均濃度の違いを調べる)
- 手法の例:ウィルコクソン順位和検定など
- 仕組み:データそのものの値ではなく、データの順位(ランキング)を使って検定を行う。NDsはすべて最低順位または同順位として扱われる。
- メリット:分布の仮定が不要で柔軟性が高いが、定量的な情報の一部が失われる。
おすすめの方法:NDsの割合に応じた選択
どの方法を選ぶかは、データ全体に占めるNDsの割合によって判断するのが実用的である。
| NDsの割合 | 最もおすすめの方法 | 次善の策 |
| 5%未満 | LOD/$\sqrt{2}$で代入 | LOD/2で代入 |
| 5%〜50% | 最大尤度推定 (MLE) | ノンパラメトリック検定 |
| 50%超 | 検出/非検出の二値データとして処理 | 統計的な定量分析は難しいと判断 |
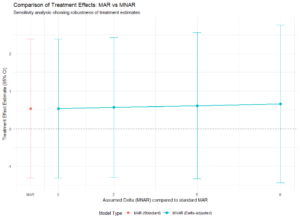
💡 感度分析を実施しよう
結論を出す前に、可能であれば「LOD/2代入」と「MLE」など複数の方法で分析を行い、結果が大きく変わらないかを確認すべきである。これにより、結論の信頼性が格段に向上する。
まとめ:統計学的な誠実さが分析の鍵
検出限界以下の値をどう扱うかは、分析者の統計学的な誠実さが問われるポイントである。
安易な「0」や「LOD」への代入は、間違った結論へと繋がるリスクがある。特にNDsの割合が高い場合は、最大尤度推定(MLE)のような、より高度で信頼性の高い統計的手法を用いることが強く推奨される。
この知識を活かし、データ分析の質をさらに高めるべきである。





コメント