R で形態素解析を行い、外部変数との対応分析を実行し、バイプロット(biplot)を書く方法の解説
前準備:データの読み込みから外部変数で分割したファイルの保存
テキストデータは、例えば、以下のようなデータを準備する
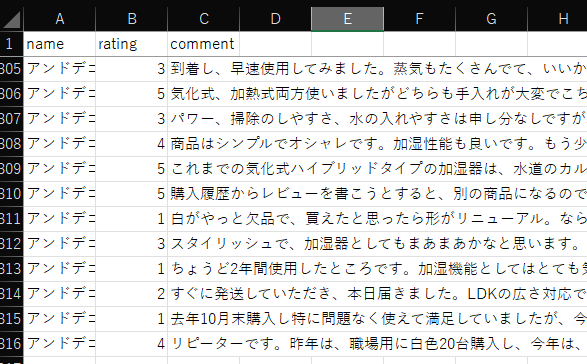
ここで、comment が分析対象のテキスト列、name が外部変数である
外部変数は、3 種類のカテゴリである
データは、例えば、以下のように、readxl パッケージの read_excel 関数を使って読み込む
library(readxl)
Dataset <- read_excel("20201121 Air Purifier Humidifier Review.xlsx")もし、外部変数が文字型(chr)として認識されている場合は、因子型(Factor)に変更する
# name の変数型を因子型に変更
library(magrittr)
Dataset %<>%
mutate(name = as.factor(name))データセットの要約を見てみる
# データセット要約
library(dplyr)
Dataset %>%
select(name:rating) %>%
summary()出力は以下のとおり
> Dataset %>%
+ select(name:rating) %>%
+ summary()
name rating
アイリスオーヤマ :105 Min. :1.000
アンドデコ :105 1st Qu.:1.000
プラズマクラスター:105 Median :4.000
Mean :3.044
3rd Qu.:5.000
Max. :5.000 次に、外部変数のカテゴリを Items というオブジェクトに格納する
# 外部変数のカテゴリを格納
Items <- Dataset %>%
use_series(name) %>%
levels()ここで、外部変数のカテゴリごとに処理を適用する関数 map を使う
例えば、Dataset 内の name の一つ一つに NROW を適用する(行数を表示する)と、
# 外部変数のカテゴリごとに関数の適用
library(purrr)
Items %>%
map(
~filter(Dataset, name==.x) %>%
NROW()
)出力は以下のとおりになる
> Items %>%
+ map(
+ ~filter(Dataset, name==.x) %>%
+ NROW()
+ )
[[1]]
[1] 105
[[2]]
[1] 105
[[3]]
[1] 105この map 関数は、apply 関数のように、カテゴリそれぞれに何か処理を行うという機能を持つ
カテゴリそれぞれで処理を施すことができる機能を使って、カテゴリ 3 種別に、テキストを分けて、ファイルに出力する
出力先は、Windows で言えば、ドキュメントフォルダの下の、AirPurifier という新しく作ったフォルダにする
# 外部変数で分割したファイルを指定のディレクトリに格納
setwd("~/AirPurifier")
Items %>%
map(
~filter(Dataset, name==.x) %>% {
tmp <- use_series(data=., comment) %>%
as.character()
writeLines(text=tmp, con=paste0("Item",(1:3)[Items==.x],".txt"))
}
)こうすると、AirPurifier というフォルダに Item1.txt, Item2.txt, Item3.txt というテキストファイルが作られる
これらの中身は、カテゴリそれぞれの comment テキストが格納されている
形態素解析(単語の抽出)と対応分析のための行列準備
次に、形態素解析、つまり、文章から単語の抽出を行う
まだ、MeCab や RMeCab の設定が終わっていなければ、以下の記事を参照して、設定する

# 形態素解析
library(RMeCab)
AP <- docDF(".", type=1, pos=c("名詞","動詞","形容詞"))
AP2 <- AP %>%
filter(POS2 %in% c("一般","固有","自立"))
AP3 <- AP2 %>%
filter(! TERM %in% c("ある","いう","いる","する","できる","なる","思う"))
まず、docDF で、形態素(単語)分析をするので、type=1 で、取り出す品詞は、例えば、名詞、動詞、形容詞とする
docDF のカッコ内の最初にある、”.” は、現在のディレクトリにあるファイルを使ってくださいという意味である
現在のディレクトリは、AirPurifier という名前のディレクトリで、その中にあるテキストファイルを使用する指示になる
処理した結果を AP に格納したので、AP の先頭部分を見てみると、以下のように出力される
TERM が単語、POS1 が品詞、POS2 が品詞詳細、Item1.txt, Item2.txt, Item3.txt が外部変数カテゴリそれぞれにおける comment テキストでの出現頻度である
> head(AP)
TERM POS1 POS2 Item1.txt Item2.txt Item3.txt
1 ! 名詞 サ変接続 0 0 1
2 # 名詞 サ変接続 0 1 0
3 % 名詞 サ変接続 1 29 5
4 %( 名詞 サ変接続 0 1 0
5 %) 名詞 サ変接続 0 1 0
6 %、 名詞 サ変接続 0 1 0次に、POS2 という変数に 一般・固有・自立 が 含まれている行だけを取り出すフィルターをかけて AP2 を作る
> head(AP2)
TERM POS1 POS2 Item1.txt Item2.txt Item3.txt
128 A 名詞 一般 4 0 0
129 C 名詞 一般 1 0 0
130 CM 名詞 一般 0 0 2
131 DE 名詞 一般 0 0 1
132 Err 名詞 一般 0 2 0
134 HP 名詞 一般 1 0 0さらに、ある・いう・いる・する・できる・なる・思う、という頻出するが、あまり、意味を持たない動詞を削除して AP3 という名前を付けている
この段階で、AP3 は、1496 行ある
それだけたくさんの単語が抽出されている
ただし、出現頻度が小さい単語はあまり特徴を見るのには適切ではない
ある程度、出現頻度が高い単語に絞るのがよい
出現頻度の下限を探るために、3 グループを通しての出現頻度を計算してみる
AP3[, -(1:3)] は、後ろから 1 列目から 3 列目を使うという意味で、Item1.txt, Item2.txt, Item3.txt の 3 列を指している
# 対応分析に向けて絞り込み
AP3$SUMS <- rowSums(AP3[,-(1:3)])
table(AP3$SUMS)
頻度一覧を見てみると、1 から 154 まで幅広く分布していることがわかる
> table(AP3$SUMS)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
770 264 110 76 55 34 20 31 17 16 8 9 8 7 7 5 4
18 19 20 21 22 23 24 25 26 27 28 29 30 31 33 34 36
4 1 3 5 2 1 2 2 1 3 1 1 1 3 1 2 1
39 40 41 47 51 54 55 59 64 77 80 86 87 98 119 124 140
1 1 3 1 1 1 1 1 1 1 1 2 1 1 1 1 1
154
1 ここから出現頻度下限を決めるかは、決まった方法はないが、一つの図に 50 個程度の単語であると、見通しがきいて興味深い図になるという感覚から、50 単語くらいになる区切りを見つける
今回の場合は、ちょうど 20 回以上とすると、50 単語になる
> table(AP3$SUMS>=20)
FALSE TRUE
1446 50 なので、20 回以上出現した単語だけに絞ることにする
AP4 <- AP3 %>%
filter(SUMS >= 20)
AP4$TERM絞った後の単語群は、以下のとおり
> AP4$TERM
[1] "いい" "つく" "ない" "よい"
[5] "わかる" "タンク" "ハイブリッド" "ヒーター"
[9] "フィルター" "リビング" "他" "使う"
[13] "使える" "価格" "値段" "入る"
[17] "入れる" "出る" "出来る" "分かる"
[21] "効果" "商品" "場所" "大きい"
[25] "安い" "容量" "寝る" "寝室"
[29] "届く" "感じ" "持つ" "書く"
[33] "月" "本体" "気" "水"
[37] "湿度" "空気" "置く" "自動"
[41] "良い" "花粉" "蒸気" "見る"
[45] "言う" "買う" "部屋" "電源"
[49] "音" "高い" このセクションの最後に、現在データフレームの AP4 を行列に変換する
# データフレームから行列に変換
library(stringr)
colnames(AP4)
## 数値列だけ選択
AP5 <- AP4 %>% select(matches("Item\\d"))
## 列名を設定
colnames(AP5) <- Items
## 行名を設定
rownames(AP5) <- AP4$TERM
## 次元の確認
dim(AP5)ここまでで、AP4 は、以下のように、単語の種類と、どのテキストファイル(3 つの外部変数カテゴリ)で、何回出現しているかの情報が入っている
> head(AP4)
TERM POS1 POS2 Item1.txt Item2.txt Item3.txt SUMS
199 いい 形容詞 自立 12 17 22 51
372 つく 動詞 自立 3 9 10 22
399 ない 形容詞 自立 12 47 39 98
481 よい 形容詞 自立 6 9 5 20
487 わかる 動詞 自立 10 8 13 31
654 タンク 名詞 一般 13 24 43 80このうち、Item1.txt, Item2.txt, Item3.txt とある列だけ取り出す
これが対応分析を行う元となるデータで、この部分を行列に変換する
上記スクリプトを実行して、AP5 を見てみると、以下のようになっている
> head(AP5)
アイリスオーヤマ アンドデコ プラズマクラスター
いい 12 17 22
つく 3 9 10
ない 12 47 39
よい 6 9 5
わかる 10 8 13
タンク 13 24 43先ほどは、Item1.txt, Item2.txt, Item3.txt となっていた列名であるが、ここで、3 つのカテゴリ名を付けた
ここまでで、AP5 は、50 行 x 3 列の行列になった
対応分析の実施とバイプロットの描画
最後に対応分析の実施とバイプロットの描画を説明する
まず、対応分析を FactoMineR パッケージの CA 関数で実行する
ここでは、図の描画を行わず、別の関数で図の描画を行う
## 対応分析のみ(図はここでは描かない)
library(FactoMineR)
AP5.CA <- CA(AP5, graph=FALSE)
summary(AP5.CA)分析結果のサマリーを見てみると以下のように出力される
> summary(AP5.CA)
Call:
CA(X = AP5, graph = FALSE)
The chi square of independence between the two variables is equal to 642.067 (p-value = 7.370266e-81 ).
Eigenvalues
Dim.1 Dim.2
Variance 0.209 0.066
% of var. 76.016 23.984
Cumulative % of var. 76.016 100.000
Rows (the 10 first)
Iner*1000 Dim.1 ctr cos2 Dim.2 ctr cos2
いい | 0.756 | 0.186 0.362 0.999 | -0.006 0.001 0.001 |
つく | 0.392 | 0.030 0.004 0.021 | -0.202 0.583 0.979 |
ない | 1.731 | -0.112 0.254 0.306 | -0.169 1.822 0.694 |
よい | 0.740 | -0.045 0.008 0.024 | 0.290 1.096 0.976 |
わかる | 1.877 | 0.341 0.738 0.821 | 0.159 0.509 0.179 |
タンク | 4.108 | 0.250 1.022 0.520 | -0.240 2.993 0.480 |
ハイブリッド | 10.232 | -1.067 4.895 0.999 | -0.030 0.012 0.001 |
ヒーター | 13.713 | -1.086 6.528 0.994 | 0.083 0.121 0.006 |
フィルター | 6.256 | 0.386 1.191 0.398 | -0.475 5.718 0.602 |
リビング | 1.265 | -0.337 0.513 0.846 | -0.144 0.296 0.154 |
Columns
Iner*1000 Dim.1 ctr cos2 Dim.2 ctr cos2
アイリスオーヤマ | 75.448 | 0.406 16.072 0.445 | 0.453 63.560 0.555 |
アンドデコ | 119.996 | -0.531 57.453 1.000 | 0.005 0.014 0.000 |
プラズマクラスター | 79.295 | 0.386 26.475 0.697 | -0.254 36.426 0.303 |Dim.1 と Dim.2 というのが、第一成分、第二成分と呼ばれるもので、プロットの座標になる
この数値自体は相対的な意味合いだけなので、絶対値で何か判断できるものではない
そして、以下の 2軸の図、バイプロット(バイは 2 つという意味)を書いて、傾向を見て取るということになる。
## バイプロット
library(factoextra)
fviz_ca_biplot(AP5.CA)バイプロットは、以下のように書かれる
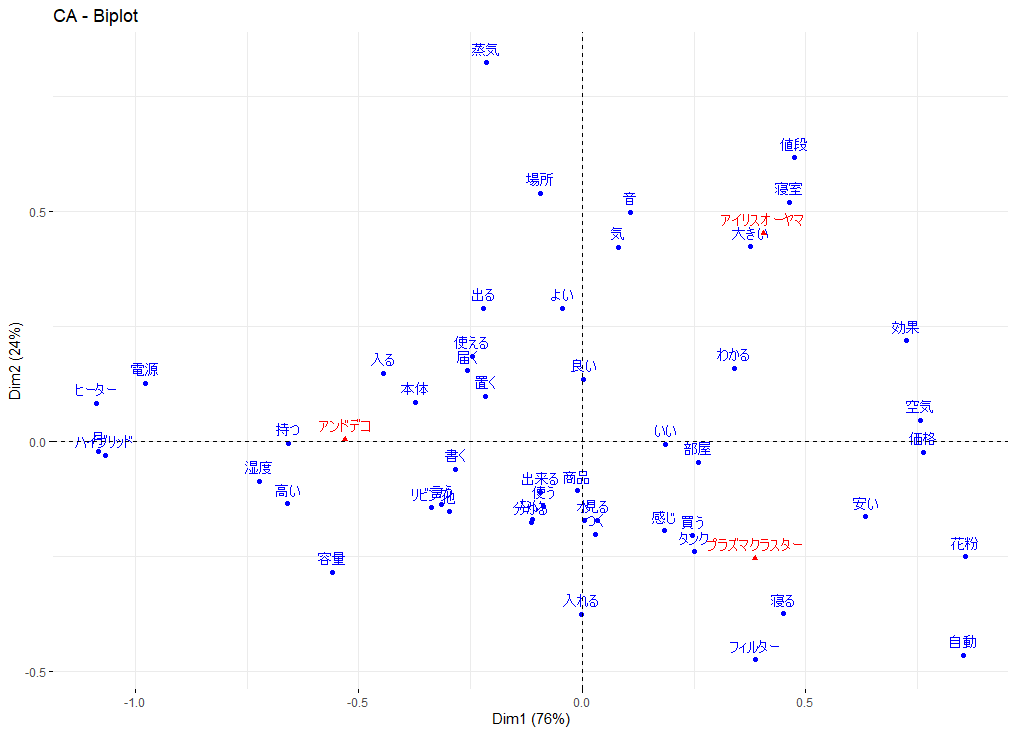
軸に書いてある % の数値の意味は、横軸は、解析した行列データ(AP5)のばらつきの 76 % を、縦軸は、ばらつきの 24 % を占めているという意味である
そして、横軸と縦軸が何を示しているかは、分析者が想像をめぐらすという見方になる
単語からは、軸の傾向は、見て取れないが、あなたなら、どのような見方をするだろうか
千差万別なので、正解はない
一方で、赤で書いてある 3 つの外部変数であるが、アイリスオーヤマとプラズマクラスターとある 2 つは空気清浄機で、アンドデコは加湿器であるため、横軸は、機能の違いそのものかもしれない
では、縦軸は、どうかと言えば、リーズナブルな価格でシンプル vs 高くて高機能 というような軸かもしれない
青の単語と赤の外部変数の関係性でも読み取りをして、想像を膨らませるとよい
外部変数の周辺に集まっているかどうかは、直接的には関係ないが、その方向にある単語は、外部変数カテゴリで発せられがちな単語と読み取ればよい
プラズマクラスターの方向には、自動・フィルター・花粉 などが目に付く
アイリスオーヤマの方向には、値段・寝室・音・大きいなどが目に入る
アンドデコの方向には、湿度・高い・リビングなどが特徴と思われる
このように、対応分析は、何か検証的な分析というわけではないものの、単語の出現が外部変数との関係性において、どのような傾向があるかを、可視化することができるという点で、興味深い分析方法である
まとめ
R でテキストマイニング(形態素解析)を行い、対応分析を実施し、バイプロットを書く方法を解説した
外部変数との関係性を見られる興味深い分析方法である
参考になれば








コメント