オッズ比の95%信頼区間が1をまたいでいないことと、有意水準5%で統計学的有意であることはイコールである。
しかし、EZRでフィッシャーの正確検定を実施すると、有意確率が5%未満であるにもかかわらず、オッズ比の95%信頼区間が1をまたいでいることがある。
こんなときはどうすればいいか?
フィッシャーの正確検定とオッズ比の95%信頼区間が一致しない例
まずは一致しない例をEZRで見てみる。
題材は、こちらのサイトの「オッズ比」というセクションにある内容だ。
https://okumuralab.org/~okumura/stat/fishertest.html
まず、分割表の直接入力を選択する。
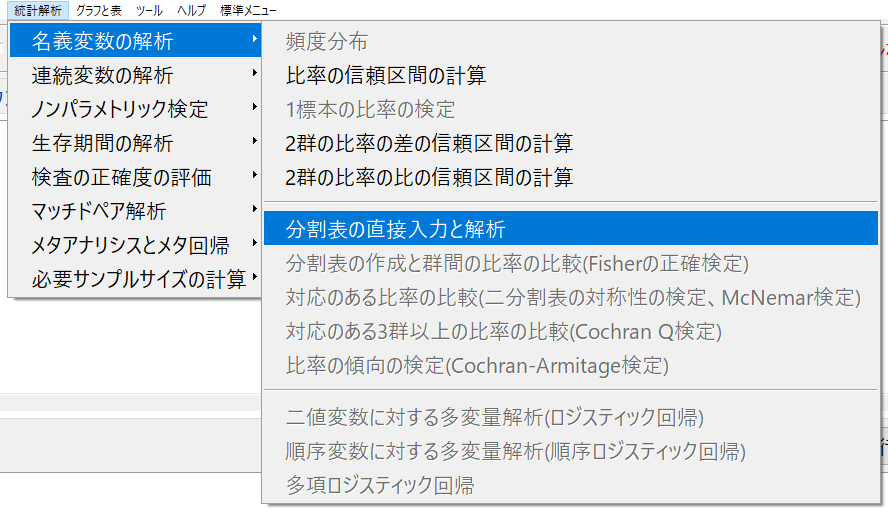
下記の図のように入力する。入力枠が出ていない場合、行か列のスライドバーを右にずらずと出現するので2x2に調節する。

OKをクリックすると結果が表示される。
確かに有意確率は0.04371で有意水準5%で統計学的有意であるが、95%信頼区間は、0.03888003から1.05649145となっており、1をまたいでしまっていて、統計学的有意に1と異なるとは言えない状態である。
> fisher.test(.Table)
Fisher's Exact Test for Count Data
data: .Table
p-value = 0.04371
alternative hypothesis: true odds ratio is not equal to 1
95 percent confidence interval:
0.03888003 1.05649145
sample estimates:
odds ratio
0.2189021
フィッシャーの正確検定とオッズ比の95%信頼区間が一致しないことがある原因
フィッシャーの正確検定では統計学的有意なのに、オッズ比の95%信頼区間が1をまたいでいる原因は、フィッシャーの正確検定の有意確率の求め方が3つあるからである。
フィッシャーの正確検定の有意確率の求め方は以下の3つある。
- 観察された分割表と等しいか小さい確率の分割表すべての確率を足し合わせる方法(”minlike”とする。minimum likelihoodの意味)
- 観察された分割表と等しいか小さい確率の分割表の確率の合計で小さいほう(一番小さい例数のセルからどんどん小さくすると一番小さい確率になる)の片側確率を2倍する方法(”central”とする)
- Blakerの正確検定で、観察された分割表と等しいか小さい確率の分割表の確率と最大となる側の確率(ただし観察された分割表よりは確率は小さい)ものの合計(”blaker”とする)
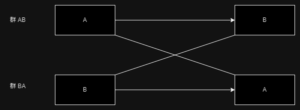
フィッシャーの正確検定の有意確率は、2×2の周囲の小計(行計及び列計)が固定された条件で、一つのセルだけを変化させて、より極端な分割表を発生させ、その分割表の発生確率を計算して足し合わせていく。
より極端という「側」に、小さくする方向か、大きくする方向か、2 方向あるわけだが、そのどちらをどのように合計するかによって3通りあるというわけだ。
フィッシャーの正確検定とオッズ比の95%信頼区間の統計学的有意性の結果を一致させるには?
EZRのfisher.test()では、minlike, central, blakerの選択はできないのだが、exact2x2 パッケージをインストールして、fisher.exact()を使うと選択ができるようになる。
そして先ほどの”central”を選ぶと一致する。
もしくは”minlike”を選択すると、95%信頼区間を計算しなおしてくれる。
まず、exact2x2 パッケージをインストールする。
install.packages("exact2x2")
インストールは1回でOK。
exact2x2 パッケージを呼び出すためにlibrary()を実行する。
library(exact2x2)
これはEZRを起動後、exact2x2 パッケージを使用する場合はいつも、事前に1回実行する必要がある。
これでパッケージを使える準備ができる。
そうしたら、先ほど実行したfisher.test()の一部を活用して、再度実行する。
実行する関数はfisher.exact()。
tsmethodというオプションで”central”を指定する。
fisher.exact(.Table, tsmethod="central")
結果は、有意確率が0.06059になり、有意水準5%では統計学的有意ではなく、95%信頼区間が1をまたいでいることと一致した。
> fisher.exact(.Table, tsmethod="central")
Central Fisher's Exact Test
data: .Table
p-value = 0.06059
alternative hypothesis: true odds ratio is not equal to 1
95 percent confidence interval:
0.03888003 1.05649145
sample estimates:
odds ratio
0.2189021
ちなみに、fisher.exact()のデフォルトは、tsmethod=”minlike”で、何も指定しなくてもminlikeで計算してくれる。
そうすると今度は有意確率はそのままで、95%信頼区間の値が変化する。
> fisher.exact(.Table)
Two-sided Fisher's Exact Test (usual method using minimum likelihood)
data: .Table
p-value = 0.04371
alternative hypothesis: true odds ratio is not equal to 1
95 percent confidence interval:
0.0435 0.9170
sample estimates:
odds ratio
0.2189021
minlikeの方法が正真正銘の正確な確率、正確な95%信頼区間であるなら、これでいいのかもしれない。
結果として統計学的有意であるので、ハッピーかも。
まとめ
EZRでフィッシャーの正確検定を実施すると、有意確率が5%を下回っているのに、オッズ比の95%信頼区間が1をまたいでいて、結果が不一致なことがある。
原因は、有意確率を求める方法が3通りあり、有意確率とオッズ比の95%信頼区間の算出方法が一致していないからである。
対処法は、exact2x2 パッケージをインストールし、fisher.exact() 関数を使うことである。
参考になれば。
参考ウェブサイト
https://okumuralab.org/~okumura/stat/fishertest.html
https://cran.r-project.org/web/packages/exact2x2/exact2x2.pdf






コメント